Contents
【問題】
【難易度】★★☆☆☆（やや易しい）
真空中に\( \ Q \ \mathrm {[C]} \ \)の電荷を持つ半径\( \ r \ \mathrm {[m]} \ \)の球状導体がある。ここで，真空の空間を比誘電率\( \ 2 \ \)の絶縁体の液体で満たしたとすると，静電気に関する記述として，正しいものを次の(1)～(5)うちから一つ選べ。ただし，無限遠点の電位を零電位とする。
(1) 球状導体表面の電位は，液体を満たす前の\( \ 2 \ \)倍になった。
(2) 球状導体表面の電界の強さは，液体を満たす前の\( \ 2 \ \)倍になった。
(3) 球状導体表面の電束密度は，液体を満たす前の\( \ 2 \ \)倍になった。
(4) 球状導体から出る電気力線の本数は，液体を満たす前の\( \ 2 \ \)倍になった。
(5) 球状導体の静電容量は，液体を満たす前の\( \ 2 \ \)倍になった。
【ワンポイント解説】
空間の誘電率が変化した場合の各パラメータの変化を問う問題です。
電磁気の基本公式を理解しているかどうかが問われています。
令和3年問2と似たような出題形式で，本問の方が計算量は少ないですが問われている知識は多いです。
1.クーロンの法則
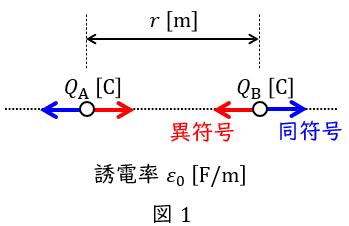
真空中で距離\( \ r \ \mathrm {[m]} \ \)離れた二つの電荷\( \ Q_{\mathrm {A}} \ \mathrm {[C]} \ \)，\( \ Q_{\mathrm {B}} \ \mathrm {[C]} \ \)に加わる力\( \ F \ \mathrm {[N]} \ \)は，真空の誘電率を\( \ \varepsilon _{0} \ \mathrm {[F / m]} \ \)とすると，
\[
\begin{eqnarray}
F &=&\frac {Q_{\mathrm {A}}Q_{\mathrm {B}}}{4\pi \varepsilon _{0}r^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。このとき，\( \ Q_{\mathrm {A}} \ \)，\( \ Q_{\mathrm {B}} \ \)の\( \ + \ \)\( \ – \ \)の符号が同符号である場合には斥力（反発する力），異符号である場合には引力（引き合う力）が働きます。
2.真空中の電界の大きさ
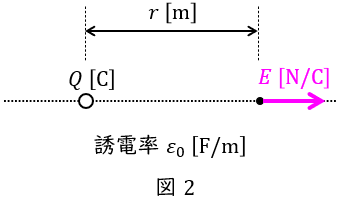
真空中に電荷\( \ Q \ \mathrm {[C]} \ \)をおいた時，電荷から距離\( \ r \ \mathrm {[m]} \ \)離れた場所の電界の大きさ\( \ E \ \mathrm {[N / C]} \ \)は，真空の誘電率を\( \ \varepsilon _{0} \ \mathrm {[F / m]} \ \)とすると，
\[
\begin{eqnarray}
E &=&\frac {Q}{4\pi \varepsilon _{0}r^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。この場所に電荷\( \ q \ \mathrm {[C]} \ \)の電荷を置けば，
\[
\begin{eqnarray}
F &=&qE \\[ 5pt ]
\end{eqnarray}
\]
の力が働きます。
3.点電荷を置いたときの周囲の電位
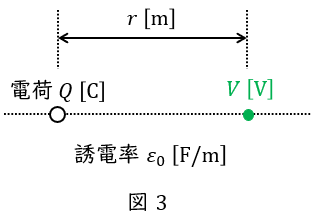
真空中に電荷\( \ Q \ \mathrm {[C]} \ \)を置いた時，距離\( \ r \ \mathrm {[m]} \ \)離れた位置の電位\( \ V \ \mathrm {[V]} \ \)は，真空の誘電率を\( \ \varepsilon _{0} \ \mathrm {[F / m]} \ \)とすると，
\[
\begin{eqnarray}
V &=&\frac {Q}{4\pi \varepsilon _{0}r} \\[ 5pt ]
\end{eqnarray}
\]
となります。クーロンの法則\( \ \displaystyle F=\frac {Q_{1}Q_{2}}{4\pi \varepsilon _{0}r^{2}} \ \)や電界の式\( \ \displaystyle E=\frac {Q}{4\pi \varepsilon _{0}r^{2}} \ \)と似ているので合わせて覚えておきましょう。
4.電気力線の特徴
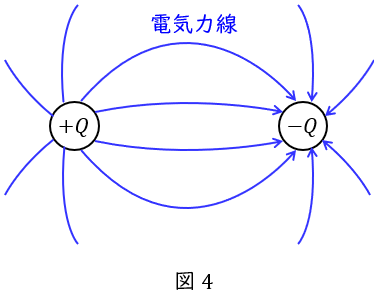
電気力線は正電荷から負電荷に向かう仮想の線で，以下のような特徴があります。言葉ではなく図で覚えておいて，内容を理解した方が良いと思います。
①電気力線の本数は電荷\( \ Q \ \mathrm {[C]} \ \)，誘電率\( \ \varepsilon \ \mathrm {[F/m]} \ \)を用いると，\( \ \displaystyle \frac {Q}{\varepsilon } \ \)本である。
②電気力線は正電荷から垂直に出て，負電荷に垂直に入る。
③電気力線同士は反発し合う。
④電気力線は枝分かれしたり，交差したりしない。
⑤電気力線の向きは電界の向きと一致し，電気力線の密度は電界の大きさに比例する。
5.電束密度\( \ D \ \)と電界\( \ E \ \)の関係
空間の誘電率を\( \ \varepsilon \ \mathrm {[F / m]} \ \)とすると，電束密度\( \ D \ \mathrm {[C / m^{2}]} \ \)と電界\( \ E \ \mathrm {[V / m]} \ \)には，
\[
\begin{eqnarray}
D&=&\varepsilon E \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。真空の誘電率を\( \ \varepsilon _{0} \ \mathrm {[F / m]} \ \)，誘電体の比誘電率を\( \ \varepsilon _{\mathrm {r}} \ \)とすると，\( \ \varepsilon = \varepsilon _{\mathrm {r}}\varepsilon _{0} \ \)の関係があるので，
\[
\begin{eqnarray}
D&=&\varepsilon _{\mathrm {r}}\varepsilon _{0}E \\[ 5pt ]
\end{eqnarray}
\]
となります。
6.電荷\( \ Q \ \)と静電容量\( \ C \ \)及び電位\( \ V \ \)の関係
空間中の静電容量\( \ C \ \mathrm {[F]} \ \)のコンデンサにおいて，蓄えられる電荷\( \ Q \ \mathrm {[C]} \ \)と導体表面の電位\( \ V \ \mathrm {[V]} \ \)には，
\[
\begin{eqnarray}
Q &=&CV \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。
【解答】
解答：(5)
(1)：誤り
ワンポイント解説「3.点電荷を置いたときの周囲の電位」の通り，電位は誘電率に反比例するので，球状導体表面の電位は，液体を満たす前の\( \ \displaystyle \frac {1}{2} \ \)倍になります。
(2)：誤り
ワンポイント解説「2.真空中の電界の大きさ」の通り，電界の強さは誘電率に反比例するので，球状導体表面の電界の強さは，液体を満たす前の\( \ \displaystyle \frac {1}{2} \ \)倍になります。
(3)：誤り
ワンポイント解説「5.電束密度\( \ D \ \)と電界\( \ E \ \)の関係」の通り，電束密度は電界の強さに比例し，電界の強さは誘電率に反比例するので，球状導体表面の電束密度は，液体を満たす前の\( \ \displaystyle \frac {1}{2} \ \)倍になります。
(4)：誤り
ワンポイント解説「4.電気力線の特徴」の通り，電気力線の密度は電界の大きさに比例し，電界の強さは誘電率に反比例するので，球状導体から出る電気力線の本数は，液体を満たす前の\( \ \displaystyle \frac {1}{2} \ \)倍になります。
(5)：正しい
ワンポイント解説「6.電荷\( \ Q \ \)と静電容量\( \ C \ \)及び電位\( \ V \ \)の関係」の通り，\( \ \displaystyle C=\frac {Q}{V} \ \)の関係があり，ワンポイント解説「3.点電荷を置いたときの周囲の電位」の式を変形すると，
\[
\begin{eqnarray}
V &=&\frac {Q}{4\pi \varepsilon _{0}r} \\[ 5pt ]
\frac {Q}{V} &=&4\pi \varepsilon _{0}r \\[ 5pt ]
C&=&4\pi \varepsilon _{0}r \\[ 5pt ]
\end{eqnarray}
\]
となるので，静電容量は誘電率に比例し，液体を満たす前の\( \ 2 \ \)倍になります。
愛知県出身 愛称たけちゃん
詳しくは