《機械》〈誘導機〉[R07上:問4]三相かご形誘導電動機の回転速度変化に伴う電流の変化に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

一般的な三相かご形誘導電動機がある。

出力が大きい定格運転条件では，誘導機の等価回路の電流は，「二次電流\(≫\)励磁電流」であるから，励磁回路を省略しても特性をほぼ表現できる。さらに，「二次抵抗による電圧降下\(≫\)その他の電圧降下」となるので，一次抵抗と漏れリアクタンスを省略しても，おおよその特性を検討できる。

このような電動機でトルク一定負荷の場合に，電流\( \ 80 \ \mathrm {A} \ \)の定格運転から電源電圧と周波数を共に\( \ 5 \ ％ \ \)下げて回転速度を少し下げた。このときの電動機の電流の値\( \ \mathrm {[A]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 72 \ \)　　(2)　\( \ 76 \ \)　　(3)　\( \ 80 \ \)　　(4)　\( \ 84 \ \)　　(5)　\( \ 88 \ \)

【ワンポイント解説】

三相かご形誘導電動機の回転速度変化に伴う電流の変化に関する問題です。
誘導機の定トルク運転時の特性の知識があれば，計算なしでも答えを導き出すことができますが，解説では定量的にトルクの導出から解を求めていきます。
本問は平成26年問4の数値を少し変更した問題となります。

1.三相誘導電動機の同期速度\( \ N_{\mathrm {s}} \ \)及び同期角速度\( \ \omega _{\mathrm {s}} \ \)
三相誘導電動機の極数が\( \ p \ \)，電源の周波数が\( \ f \ \mathrm {[Hz]} \ \)の時，同期速度\( \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \)は，
\[
\begin{eqnarray}
N_{\mathrm {s}} &=&\frac {120f}{p} \\[ 5pt ] \end{eqnarray}
\] となります。また，同期角速度\( \ \omega _{\mathrm {s}} \ \mathrm {[rad / s]} \ \)は，
\[
\begin{eqnarray}
\omega _{\mathrm {s}} &=&\frac {2\pi N_{\mathrm {s}}}{60} \\[ 5pt ] &=&\frac {2\pi }{60}\cdot \frac {120f}{p} \\[ 5pt ] &=&\frac {4\pi f}{p} \\[ 5pt ] \end{eqnarray}
\] で求められます。

2.誘導機の滑り\( \ s \ \)
誘導機の同期速度が\( \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \)，回転速度が\( \ N \ \mathrm {[{min}^{-1}]} \ \)である時，誘導機の滑り\( \ s \ \)は，
\[
\begin{eqnarray}
s &=&\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}} \\[ 5pt ] \end{eqnarray}
\] となり，これを変形すると，
\[
\begin{eqnarray}
sN_{\mathrm {s}}&=&N_{\mathrm {s}}-N \\[ 5pt ] N&=&N_{\mathrm {s}}-sN_{\mathrm {s}} \\[ 5pt ] &=& N_{\mathrm {s}}\left( 1-s\right) \\[ 5pt ] \end{eqnarray}
\] となります。

3.二次入力\( \ P_{2} \ \)と出力\( \ P_{\mathrm {o}} \ \)と二次銅損\( \ P_{\mathrm {c2}} \ \)の関係
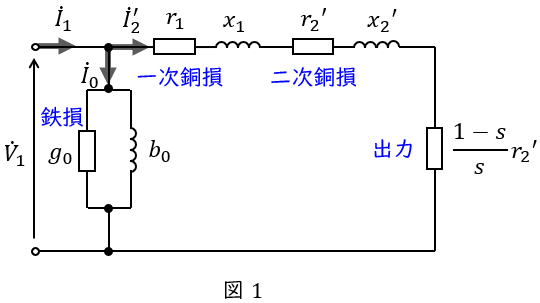
誘導電動機の\( \ \mathrm {L} \ \)形等価回路は図1のようになります。図1において，\( \ {\dot V}_{1} \ \mathrm {[V]} \ \)は一次側端子電圧，\( \ {\dot I}_{1} \ \mathrm {[A]} \ \)は一次電流，\( \ {\dot I}_{2}^{\prime } \ \mathrm {[A]} \ \)は二次電流の一次換算，\( \ {\dot I}_{0} \ \mathrm {[A]} \ \)は励磁電流，\( \ r_{1} \ \mathrm {[\Omega ]} \ \)は一次巻線抵抗，\( \ r_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)は二次巻線抵抗の一次換算，\( \ x_{1} \ \mathrm {[\Omega ]} \ \)は一次漏れリアクタンス，\( \ x_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)は二次漏れリアクタンスの一次換算，\( \ s \ \)は滑りとなります。
図1より，出力\( \ P_{\mathrm {o}} \ \mathrm {[W]} \ \)，二次銅損\( \ P_{\mathrm {c2}} \ \mathrm {[W]} \ \)，二次入力\( \ P_{2} \ \mathrm {[W]} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {o}} &=& 3\frac {1-s}{s}r_{2}^{\prime }{I_{2}^{\prime }}^{2} \\[ 5pt ] P_{\mathrm {c2}} &=& 3r_{2}^{\prime }{I_{2}^{\prime }}^{2} \\[ 5pt ] P_{2} &=& P_{\mathrm {o}}+P_{\mathrm {c2}} =3\frac {r_{2}^{\prime }}{s}{I_{2}^{\prime }}^{2} \\[ 5pt ] \end{eqnarray}
\] となり，誘導電動機の二次入力\( \ P_{2} \ \mathrm {[W]} \ \)，出力\( \ P_{\mathrm {o}} \ \mathrm {[W]} \ \)，二次銅損\( \ P_{\mathrm {c2}} \ \mathrm {[W]} \ \)には，
\[
\begin{eqnarray}
P_{2}：P_{\mathrm {o}}：P_{\mathrm {c2}} &=& 1：(1-s)：s \\[ 5pt ] \end{eqnarray}
\] の関係があることが分かります。

【解答】

解答：(3)
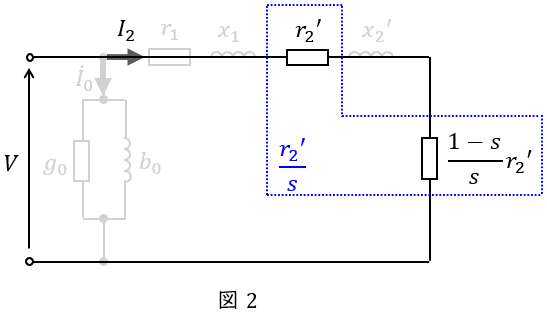
題意より，励磁回路及び一次抵抗と漏れリアクタンスは無視できるので，本問の誘導電動機の等価回路は図2のようになる。
図2において，二次電流の一次換算\( \ I_{2} \ \mathrm {[A]} \ \)を求める式より，
\[
\begin{eqnarray}
I_{2}&=&\frac {V}{\displaystyle \frac {{r_{2}}^{\prime }}{s}} \\[ 5pt ] \frac {{r_{2}}^{\prime }}{s}&=&\frac {V}{I_{2}} \\[ 5pt ] \end{eqnarray}
\] であり，二次入力\( \ P_{2} \ \mathrm {[W]} \ \)は，ワンポイント解説「3.二次入力\( \ P_{2} \ \)と出力\( \ P_{\mathrm {o}} \ \)と二次銅損\( \ P_{\mathrm {c2}} \ \)の関係」の通り，
\[
\begin{eqnarray}
P_{2} &=&3\cdot \frac {{r_{2}}^{\prime }}{s}I_{2}^{2} \\[ 5pt ] &=&3\cdot \frac {V}{I_{2}}I_{2}^{2} \\[ 5pt ] &=&3VI_{2} \\[ 5pt ] \end{eqnarray}
\] となるので，トルク\( \ T \ \mathrm {[N\cdot m]} \ \)は，同期角速度\( \ \displaystyle \omega _{\mathrm {s}}=\frac {4\pi f}{p} \ \mathrm {[rad/s]} \ \)，出力\( \ P_{\mathrm {o}} \ \mathrm {[W]} \ \)の時の角速度\( \ \omega \ \mathrm {[rad/s]} \ \)とすると，
\[
\begin{eqnarray}
T &=&\frac {P_{\mathrm {o}}}{\omega } \\[ 5pt ] &=&\frac {P_{2} (1-s)}{\omega _{\mathrm {s}} (1-s) } \\[ 5pt ] &=&\frac {P_{2}}{\omega _{\mathrm {s}}} \\[ 5pt ] &=&\frac {3VI_{2}}{\displaystyle \frac {4\pi f}{p}} \\[ 5pt ] &=&\frac {3pVI_{2}}{4\pi f} \\[ 5pt ] \end{eqnarray}
\] となる。ここで，トルク一定負荷において，電源電圧\( \ V \ \mathrm {[V]} \ \)と周波数\( \ f \ \mathrm {[Hz]} \ \)を\( \ 5 \ ％ \ \)下げた時の電流を\( \ I_{2}^{\prime } \ \mathrm {[A]} \ \)とすると，
\[
\begin{eqnarray}
\frac {3pVI_{2}}{4\pi f} &=&\frac {3p\cdot 0.95VI_{2}^{\prime}}{4\pi \cdot 0.95f} \\[ 5pt ] I_{2}&=&I_{2}^{\prime} \\[ 5pt ] \end{eqnarray}
\] の関係があるので，電流の値は変化しない\( \ \left( 80 \ \mathrm {A}\right) \ \)ことが分かる。