《法規》〈電気施設管理〉[R07上:問11]水力発電所の年間発電電力量と設備利用率に関する空欄穴埋問題

【問題】

【難易度】★★★★☆（やや難しい）

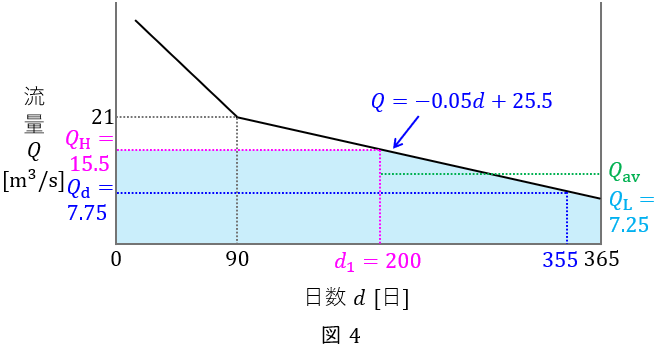
有効落差\( \ 90 \ \mathrm {m} \ \)，最大使用水量が渇水量（\( \ 1 \ \)年のうち\( \ 355 \ \)日は確保できる水量）の\( \ 2 \ \)倍，水車及び発電機の総合効率\( \ 80 \ \mathrm {％} \ \)の流込式水力発電所がある。この発電所が利用している河川の流量\( \ Q \ \mathrm {[ m^{3} / s]} \ \)が図のような年間流量曲線（日数\( \ d \ \)が\( \ 90 \ \)日以上の部分は，\( \ Q=-0.05 d+25.5 \ \)で表される。）であるとき，次の(a)及び(b)の問に答えよ。ただし，水の密度を\( \ 1 \ 000 \ \mathrm {kg/m^{3}} \ \)，重力加速度を\( \ 9.8 \ \mathrm {m/s^{2}} \ \)とする。

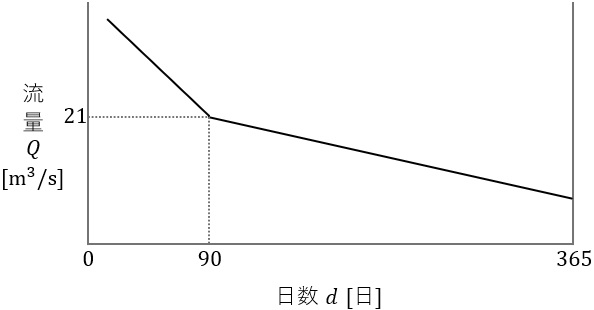
(a)　この発電所の年間可能発電電力量の値\( \ \mathrm {[GW\cdot h]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 47.9 \ \)　　(2)　\( \ 72.8 \ \)　　(3)　\( \ 84.3 \ \)　　(4)　\( \ 94.5 \ \)　　(5)　\( \ 97.4 \ \)

(b)　この発電所の設備利用率\( \ \mathrm {[％]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 50.0 \ \)　　(2)　\( \ 63.0 \ \)　　(3)　\( \ 69.5 \ \)　　(4)　\( \ 75.9 \ \)　　(5)　\( \ 88.0 \ \)

【ワンポイント解説】

与えられている流況曲線から水力発電所の年間発電電力量と設備利用率を求める問題です。
計算量が多いため，計算の得意不得意で点数差が大きく開く問題です。しっかりと中身を理解して解けるようにしておきましょう。
直近の令和6年下期問11に類題が出題されていましたので，難易度の割には正答率が高かったと予想される問題です。

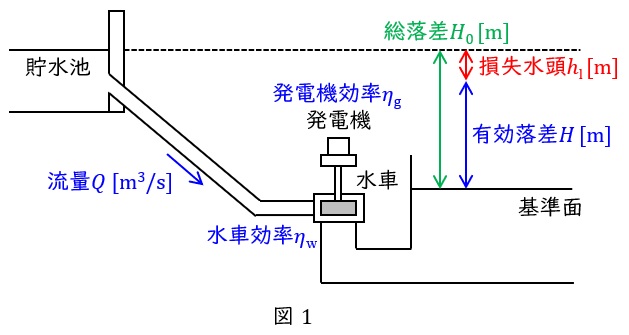
1.水力発電所の出力\( \ P \ \)
水力発電所の使用水量\( \ Q \ \mathrm {[m^{3}／s]} \ \)，有効落差\( \ H \ \mathrm {[m]} \ \)，水車効率\( \ \eta _{\mathrm {w}} \ \)，発電機効率\( \ \eta _{\mathrm {g}} \ \)とすると，発電機の出力\( \ P \ \mathrm {[kW]} \ \)は
\[
\begin{eqnarray}
P &=&9.8QH\eta _{\mathrm {w}}\eta _{\mathrm {g}} \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] で求められます。これは重力加速度\( \ g=9.8 \ \mathrm {[m／s^{2}]} \ \)及び水の密度\( \ \rho =1 \ 000 \ \mathrm {[kg／m^{3}]} \ \)を使用した時の発電機の出力である
\[
\begin{eqnarray}
P &=&\rho gQH\eta _{\mathrm {w}}\eta _{\mathrm {g}} \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}
\] に各値を代入し，
\[
\begin{eqnarray}
P &=&1 \ 000 \times 9.8 QH\eta _{\mathrm {w}}\eta _{\mathrm {g}} \ \mathrm {[W]} \\[ 5pt ] &=&9.8 QH\eta _{\mathrm {w}}\eta _{\mathrm {g}} \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] として導出したものです。

2.設備利用率
最大出力で\( \ 1 \ \)年間運転し続けた電力量に対する実際の電力量の割合です。
最大出力\( \ P \ \mathrm {[kW]} \ \)，年間発電電力量\( \ W \ \mathrm {[kW\cdot h]} \ \)であるとき，\( \ 1 \ \)日が\( \ 24 \ \)時間，\( \ 1 \ \)年が\( \ 365 \ \)日であるとすると，設備利用率\( \ \alpha \ \)は，
\[
\begin{eqnarray}
\alpha &=&\frac {W}{P\times 24 \times 365} \\[ 5pt ] \end{eqnarray}
\] で求められます。

【解答】

(a)解答：(3)
河川における渇水量\( \ Q_{\mathrm {d}} \ \mathrm {[m^{3}/s]} \ \)は，
\[
\begin{eqnarray}
Q_{\mathrm {d}} &=&-0.05 d+25.5 \\[ 5pt ] &=&-0.05 \times 355+25.5 \\[ 5pt ] &=&7.75 \ \mathrm {[m^{3}/s]} \\[ 5pt ] \end{eqnarray}
\] であり，最大使用水量\( \ Q_{\mathrm {H}} \ \mathrm {[m^{3}/s]} \ \)は，渇水量の\( \ 2 \ \)倍であるから，
\[
\begin{eqnarray}
Q_{\mathrm {H}} &=&2Q_{\mathrm {d}} \\[ 5pt ] &=&2\times 7.75 \\[ 5pt ] &=&15.5 \ \mathrm {[m^{3}/s]} \\[ 5pt ] \end{eqnarray}
\] となる。

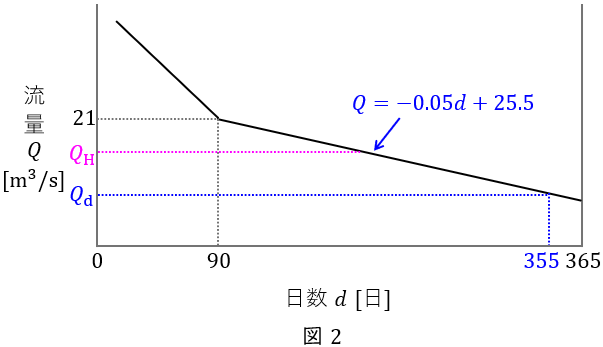
次に，最大使用水量\( \ Q_{\mathrm {H}}=15.5 \ \mathrm {[m^{3}/s]} \ \)が確保できる日数\( \ d_{1} \ \mathrm {[日]} \ \)は，
\[
\begin{eqnarray}
Q_{\mathrm {H}} &=&-0.05 d_{1}+25.5 \\[ 5pt ] 0.05 d_{1}&=&25.5-Q_{\mathrm {H}} \\[ 5pt ] d_{1}&=&\frac {25.5-Q_{\mathrm {H}}}{0.05} \\[ 5pt ] &=&\frac {25.5-15.5}{0.05} \\[ 5pt ] &=&200 \ \mathrm {[日]} \\[ 5pt ] \end{eqnarray}
\] となり，年間で最も少ない流量\( \ Q_{\mathrm {L}} \ \mathrm {[m^{3}/s]} \ \)は，
\[
\begin{eqnarray}
Q_{\mathrm {L}} &=&-0.05 d+25.5 \\[ 5pt ] &=&-0.05 \times 365+25.5 \\[ 5pt ] &=&7.25 \ \mathrm {[m^{3}/s]} \\[ 5pt ] \end{eqnarray}
\] となる。

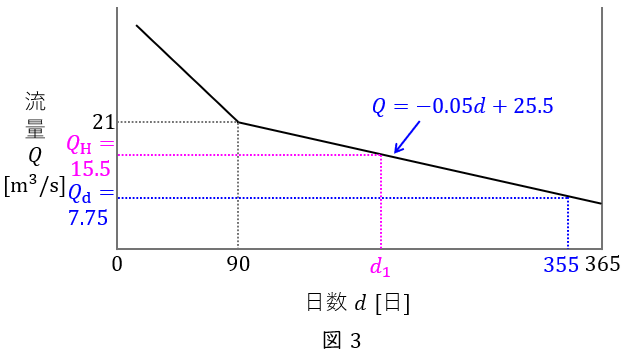
よって，年間の発電電力量は図4に示す範囲となり，最大使用水量で運転できない\( \ 200\sim 365 \ \mathrm {[日]} \ \)の平均流量\( \ Q_{\mathrm {av}} \ \mathrm {[m^{3}/s]} \ \)は，
\[
\begin{eqnarray}
Q_{\mathrm {av}} &=&\frac {Q_{\mathrm {H}}+Q_{\mathrm {L}}}{2} \\[ 5pt ] &=&\frac {15.5+7.25}{2} \\[ 5pt ] &=&11.375 \ \mathrm {[m^{3}/s]} \\[ 5pt ] \end{eqnarray}
\] となるので，年間可能発電電力量\( \ W \ \mathrm {[GW\cdot h]} \ \)は，ワンポイント解説「1.水力発電所の出力\( \ P \ \)」の通り，
\[
\begin{eqnarray}
W &=&9.8Q_{\mathrm {H}}H\eta \times 24 \times 200+9.8Q_{\mathrm {av}}H\eta \times 24 \times 165 \\[ 5pt ] &=&9.8H\eta \times 24 \left( Q_{\mathrm {H}}\times 200+Q_{\mathrm {av}} \times 165 \right) \\[ 5pt ] &=&9.8\times 90 \times 0.8 \times 24 \times \left( 15.5\times 200+11.375 \times 165 \right) \\[ 5pt ] &≒&84 \ 280 \ 000 \ \mathrm {[kW\cdot h]}　→　84.3 \ \mathrm {[GW\cdot h]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(5)
(a)解答式より，設備利用率\( \ \alpha \ \mathrm {[％]} \ \)は，ワンポイント解説「2.設備利用率」の通り，
\[
\begin{eqnarray}
\alpha &=&\frac {W}{9.8Q_{\mathrm {H}}H\eta \times 24 \times 365}\times 100 \\[ 5pt ] &=&\frac {84 \ 280 \ 000}{9.8\times 15.5\times 90\times 0.8 \times 24 \times 365}\times 100 \\[ 5pt ] &≒& 88.0 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。