《法規》〈電気施設管理〉[H27:問11]架空電線路の施設に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

図のように既設の高圧架空電線路から，電線に硬銅より線を使用した電線路を高低差なく径間\(\mathrm {40 \ m}\)延長することにした。

新設支持物に\(\mathrm {A}\)種鉄筋コンクリート柱を使用し，引留支持物とするため支線を電線路の延長方向\(\mathrm {10 \ m}\)の地点に図のように設ける。電線と支線の支持物への取付け高さはともに\(\mathrm {10 \ m}\)であるとき，次の(a)及び(b)の問に答えよ。

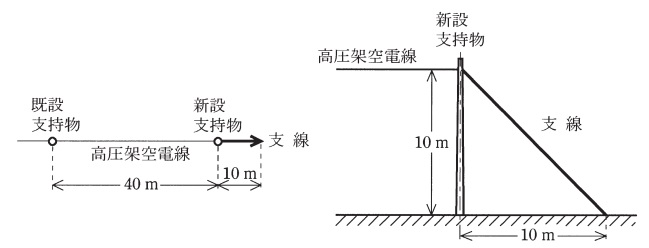
(a)　電線の水平張力を\(\mathrm {13 \ \mathrm {kN}}\)として，その張力を支線で全て支えるものとする。支線の安全率を\(\mathrm {1.5}\)としたとき，支線に要求される引張強さの最小の値\(\mathrm {[\mathrm {kN}]}\)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\(6.5\)　　(2)　\(10.7\)　　(3)　\(19.5\)　　(4)　\(27.6\)　　(5)　\(40.5\)

(b)　電線の引張強さを\(\mathrm {28.6 \ \mathrm {kN}}\)，電線の重量と風圧荷重との合成荷重を\(\mathrm {18 \ N/m}\)とし，高圧架空電線の引張強さに対する安全率を\(2.2\)としたとき，この延長した電線の弛度(たるみ)の値\(\mathrm {[\mathrm {m}]}\)は，いくら以上としなければならないか。最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\(0.14\)　　(2)　\(0.28\)　　(3)　\(0.49\)　　(4)　\(0.94\)　　(5)　\(1.97\)

【ワンポイント解説】

電線の張力とたるみの問題で，どちらも電力科目に近い問題と言えると思います。電線のたるみの公式は積分を必要とするため，三種では公式を暗記する必要があります。

1.電線の弛度，たるみ
電線\(\mathrm {1 \ \mathrm {m}}\)あたりの合成荷重を\(W \ \mathrm {[N/m]}\)，径間を\(S \ \mathrm {[m]}\)，電線の水平張力を\(T \ \mathrm {[N]}\)とした時，電線のたるみ\(D \ \mathrm {[m]}\)は，
\[
D=\frac {WS^{2}}{8T}
\] となります。

【関連する「電気の神髄」記事】

　　電線のたるみ（弛度）・実長の式

【解答】

(a)解答：(4)
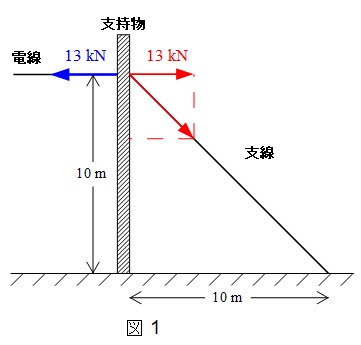
支線の取付位置と電線部の高さはともに\(\mathrm {10 \ \mathrm {m}}\)なので，電柱と支線のなす角は\(45°\)となる。
支線の張力を\(T\)とすると，支線の張力の水平成分と電線の水平張力が等しいので，
\[
\begin{eqnarray}
T\sin 45°&=&13\\[ 5pt ] T\cdot \frac {1}{\sqrt{2}}&=&13 \\[ 5pt ] T&=&13\sqrt{2} \\[ 5pt ] &≒&18.38 \ \mathrm {[kN]}
\end{eqnarray}
\] となる。安全率\(\alpha =1.5\)なので，要求される支線の引張強さ\(T_{0}\)は，
\[
\begin{eqnarray}
T_{0}&=&18.38\times 1.5\\[ 5pt ] &≒&27.6 \ \mathrm {[kN]}
\end{eqnarray}
\] と求められる。

(b)解答：(2)
電線の引張強さが\(\mathrm {28.6 \ \mathrm {kN}}\)，安全率が\(2.2\)なので，電線の許容最大張力\(T_{\mathrm {m}}\)は，
\[
\begin{eqnarray}
T_{\mathrm {m}}&=&\frac {28.6}{2.2}\\[ 5pt ] &=&13 \ \mathrm {[kN]}
\end{eqnarray}
\] となる。よって，ワンポイント解説「1.電線の弛度，たるみ」より電線の弛度(たるみ)\(D\)は，
\[
\begin{eqnarray}
D&=&\frac {WS^{2}}{8T_{\mathrm {m}}} \\[ 5pt ] &=&\frac {18 \times 40^{2}}{8\times 13\times 10^{3}} \\[ 5pt ] &≒&0.28 \ \mathrm {[m]}
\end{eqnarray}
\] と求められる。