《理論》〈電磁気〉[H25:問2]点電荷に働くクーロンの法則に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

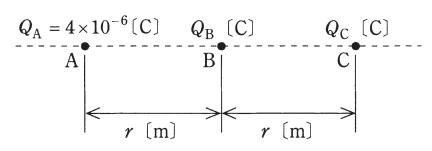
図のように，真空中の直線上に間隔\( \ r \ \mathrm {[m]} \ \)を隔てて，点\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)，\( \ \mathrm {C} \ \)があり，各点に電気量\( \ Q_{\mathrm {A}}=4\times 10^{-6} \ \mathrm {[C]} \ \)，\( \ Q_{\mathrm {B}} \ \mathrm {[C]} \ \)，\( \ Q_{\mathrm {C}} \ \mathrm {[C]} \ \)の点電荷を置いた。これら三つの点電荷に働く力がそれぞれ零になった。このとき，\( \ Q_{\mathrm {B}} \ \mathrm {[C]} \ \)及び\( \ Q_{\mathrm {C}} \ \mathrm {[C]} \ \)の値の組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。
ただし，真空の誘電率を\( \ \varepsilon _{0} \ \mathrm {[F/m]} \ \)とする。

\[
\begin{array}{ccc}
& Q_{\mathrm {B}} & Q_{\mathrm {C}} \\
\hline
(1) & 1\times 10^{-6} & -4\times 10^{-6} \\
\hline
(2) & -2\times 10^{-6} & 8\times 10^{-6} \\
\hline
(3) & -1\times 10^{-6} & 4\times 10^{-6} \\
\hline
(4) & 0 & -1\times 10^{-6} \\
\hline
(5) & -4\times 10^{-6} & 1\times 10^{-6} \\
\hline
\end{array}
\]

【ワンポイント解説】

クーロンの法則を利用した問題です。試験当日，導出過程が不明であれば，解答群の値を代入して，各電荷にかかる力が零になるものを選択すれば良いです。

1.クーロンの法則
真空中で距離\( \ r \ \)離れた二つの電荷\( \ Q_{\mathrm {A}} \ \)，\( \ Q_{\mathrm {B}} \ \)に加わる力\( \ F \ \)は，真空の誘電率を\( \ \varepsilon _{0} \ \)とすると，
\[
\begin{eqnarray}
F &=&\frac {Q_{\mathrm {A}}Q_{\mathrm {B}}}{4\pi \varepsilon _{0}r^{2}} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(3)
問題図において右方向にかかる力を正とする。ワンポイント解説「1.クーロンの法則」より，点電荷\( \ Q_{\mathrm {B}} \ \)にかかる力の大きさ\( \ F_{\mathrm {B}} \ \)は，
\[
\begin{eqnarray}
F_{\mathrm {B}} &=&\frac {Q_{\mathrm {A}}Q_{\mathrm {B}}}{4\pi \varepsilon _{0}r^{2}}-\frac {Q_{\mathrm {B}}Q_{\mathrm {C}}}{4\pi \varepsilon _{0}r^{2}} \\[ 5pt ] &=&\frac {Q_{\mathrm {B}}}{4\pi \varepsilon _{0}r^{2}}\left( Q_{\mathrm {A}}-Q_{\mathrm {C}}\right) \\[ 5pt ] \end{eqnarray}
\] となり，\( \ F_{\mathrm {B}}=0 \ \)であるから，
\[
\begin{eqnarray}
\frac {Q_{\mathrm {B}}}{4\pi \varepsilon _{0}r^{2}}\left( Q_{\mathrm {A}}-Q_{\mathrm {C}}\right) &=&0 \\[ 5pt ] Q_{\mathrm {A}}-Q_{\mathrm {C}}&=&0 \\[ 5pt ] Q_{\mathrm {A}}&=&Q_{\mathrm {C}} \\[ 5pt ] \end{eqnarray}
\] となり，\( \ Q_{\mathrm {C}}=4\times 10^{-6} \ \mathrm {[C]} \ \)と求められる。(この時点で解答は(3)と確定します)

次に\( \ Q_{\mathrm {C}} \ \)にかかる力の大きさ\( \ F_{\mathrm {C}} \ \)は，
\[
\begin{eqnarray}
F_{\mathrm {C}}&=&\frac {Q_{\mathrm {A}}Q_{\mathrm {C}}}{4\pi \varepsilon _{0}\left( 2r\right) ^{2}}+\frac {Q_{\mathrm {B}}Q_{\mathrm {C}}}{4\pi \varepsilon _{0}r^{2}} \\[ 5pt ] &=&\frac {Q_{\mathrm {A}}Q_{\mathrm {C}}}{16\pi \varepsilon _{0}r^{2}}+\frac {Q_{\mathrm {B}}Q_{\mathrm {C}}}{4\pi \varepsilon _{0}r^{2}} \\[ 5pt ] &=&\frac {Q_{\mathrm {C}}}{4\pi \varepsilon _{0}r^{2}}\left( \frac {Q_{\mathrm {A}}}{4}+Q_{\mathrm {B}}\right) \\[ 5pt ] \end{eqnarray}
\] となり，\( \ F_{\mathrm {C}}=0 \ \)であるから，整理して値を代入すると，
\[
\begin{eqnarray}
\frac {Q_{\mathrm {C}}}{4\pi \varepsilon _{0}r^{2}}\left( \frac {Q_{\mathrm {A}}}{4}+Q_{\mathrm {B}}\right) &=&0 \\[ 5pt ] \frac {Q_{\mathrm {A}}}{4}+Q_{\mathrm {B}}&=&0 \\[ 5pt ] Q_{\mathrm {B}}&=&-\frac {Q_{\mathrm {A}}}{4} \\[ 5pt ] &=&-\frac {4\times 10^{-6}}{4} \\[ 5pt ] &=&-1\times 10^{-6} \ \mathrm {[C]} \\[ 5pt ] \end{eqnarray}
\] と求められる。