《理論》〈電気回路〉[H24:問5]電圧源と電流源の等価変換に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

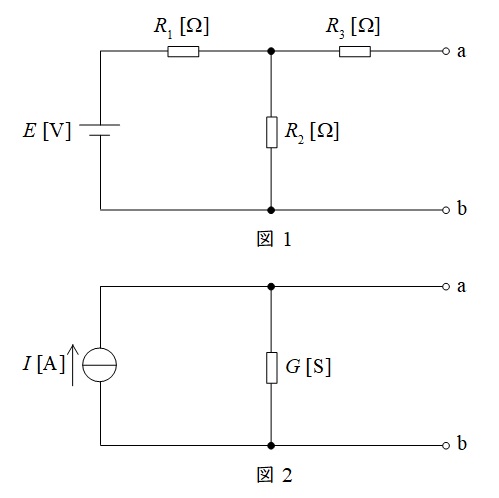
図1のように電圧が\( \ E \ \mathrm {[V]} \ \)の直流電圧源で構成される回路を，図2のように電流が\( \ I \ \mathrm {[A]} \ \)の直流電流源（内部抵抗が無限大で，負荷変動があっても定電流を流出する電源）で構成される等価回路に置き替えることを考える。この場合，電流\( \ I \ \mathrm {[A]} \ \)の大きさは図1の端子\( \ \mathrm {a－b} \ \)を短絡したとき，そこを流れる電流の大きさに等しい。また，図2のコンダクタンス\( \ G \ \mathrm {[S]} \ \)の大きさは図1の直流電圧源を短絡し，端子\( \ \mathrm {a－b} \ \)からみたコンダクタンスの大きさに等しい。\( \ I \ \mathrm {[A]} \ \)と\( \ G \ \mathrm {[S]} \ \)の値を表す式の組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。

\[
\begin{array}{ccc}
& I \ \mathrm {[A]} & G \ \mathrm {[S]} \\
\hline
(1) & \displaystyle \frac {R_{1}}{R_{1}R_{2}+R_{2}R_{3}+R_{3}R_{1}}E & \displaystyle \frac {R_{2}+R_{3}}{R_{1}R_{2}+R_{2}R_{3}+R_{3}R_{1}} \\
\hline
(2) & \displaystyle \frac {R_{2}}{R_{1}R_{2}+R_{2}R_{3}+R_{3}R_{1}}E & \displaystyle \frac {R_{1}+R_{2}}{R_{1}R_{2}+R_{2}R_{3}+R_{3}R_{1}} \\
\hline
(3) & \displaystyle \frac {R_{2}}{R_{1}R_{2}+R_{2}R_{3}+R_{3}R_{1}}E & \displaystyle \frac {R_{2}+R_{3}}{R_{1}R_{2}+R_{2}R_{3}+R_{3}R_{1}} \\
\hline
(4) & \displaystyle \frac {R_{1}}{R_{1}R_{2}+R_{2}R_{3}+R_{3}R_{1}}E & \displaystyle \frac {R_{1}+R_{2}}{R_{1}R_{2}+R_{2}R_{3}+R_{3}R_{1}} \\
\hline
(5) & \displaystyle \frac {R_{3}}{R_{1}R_{2}+R_{2}R_{3}+R_{3}R_{1}}E & \displaystyle \frac {R_{1}+R_{2}}{R_{1}R_{2}+R_{2}R_{3}+R_{3}R_{1}} \\
\hline
\end{array}
\]

【ワンポイント解説】

計算問題が得意な方には非常に易しい問題，苦手な方には難しい問題となると思います。特別な公式は必要ないので問題文の説明に沿って丁寧に解くようにしましょう。

1.合成抵抗
抵抗\( \ R_{1} \ \)と\( \ R_{2} \ \)が与えられている時，それぞれの合成抵抗\( \ R \ \)は以下の式で与えられます。

①直列
直列合成抵抗\( \ R \ \)は，
\[
\begin{eqnarray}
R&=&R_{1}+R_{2} \\[ 5pt ] \end{eqnarray}
\] となります。

②並列
並列合成抵抗\( \ R \ \)は，
\[
\begin{eqnarray}
\frac {1}{R}&=&\frac {1}{R_{1}}+\frac {1}{R_{2}} \\[ 5pt ] \end{eqnarray}
\] となり，整理すると，
\[
\begin{eqnarray}
R&=&\frac {R_{1}R_{2}}{R_{1}+R_{2}} \\[ 5pt ] \end{eqnarray}
\] となります。

2.分圧・分流の法則
①分圧の法則
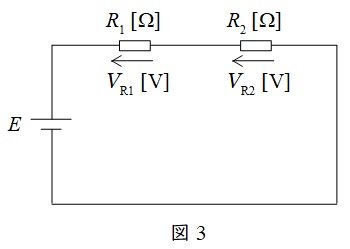
図3に示した直列回路において，各抵抗にかかる電圧は以下の通りとなります。
\[
\begin{eqnarray}
V_{\mathrm {R1}}&=&\frac {R_{1}}{R_{1}+R_{2}}E \\[ 5pt ] V_{\mathrm {R2}}&=&\frac {R_{2}}{R_{1}+R_{2}}E \\[ 5pt ] \end{eqnarray}
\]

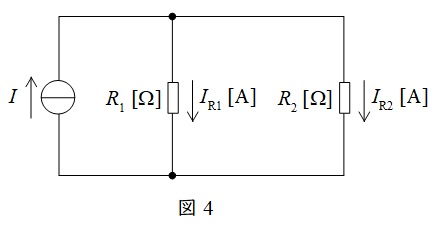
②分流の法則
図4に示した並列回路において，各抵抗に流れる電流は以下の通りとなります。分子の抵抗が分圧の法則と逆となることに注意して下さい。
\[
\begin{eqnarray}
I_{\mathrm {R1}}&=&\frac {\color{red}{R_{2}}}{R_{1}+R_{2}}I \\[ 5pt ] I_{\mathrm {R2}}&=&\frac {\color{red}{R_{1}}}{R_{1}+R_{2}}I \\[ 5pt ] \end{eqnarray}
\]

【解答】

解答：(2)
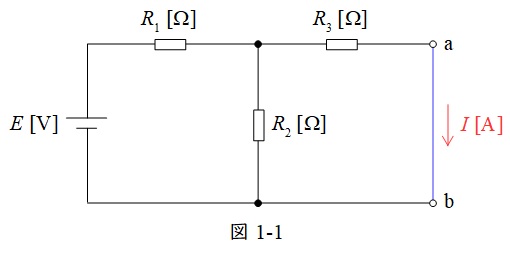
問題文より，「電流\( \ I \ \mathrm {[A]} \ \)の大きさは図1の端子\( \ \mathrm {a－b} \ \)を短絡したとき，そこを流れる電流の大きさに等しい」ので，題意に沿って図を描くと図1-1の通りとなる。そして，図1-1の短絡した部分が\( \ I \ \mathrm {[A]} \ \)の大きさとなる。
図1-1の\( \ R_{2} \ \)と\( \ R_{3} \ \)の合成抵抗\( \ R_{23} \ \)は，ワンポイント解説「1.合成抵抗」より，
\[
\begin{eqnarray}
R_{23}&=&\frac {R_{2}R_{3}}{R_{2}+R_{3}} \\[ 5pt ] \end{eqnarray}
\] となり，\( \ R_{1} \ \)も含めた合成抵抗\( \ R_{0} \ \)は，
\[
\begin{eqnarray}
R_{0}&=&R_{1}+R_{23} \\[ 5pt ] &=&R_{1}+\frac {R_{2}R_{3}}{R_{2}+R_{3}} \\[ 5pt ] &=&\frac {R_{1}\left( R_{2}+R_{3}\right) +R_{2}R_{3}}{R_{2}+R_{3}} \\[ 5pt ] &=&\frac {R_{1}R_{2}+R_{3}R_{1}+R_{2}R_{3}}{R_{2}+R_{3}} \\[ 5pt ] &=&\frac {R_{1}R_{2}+R_{2}R_{3}+R_{3}R_{1}}{R_{2}+R_{3}} \\[ 5pt ] \end{eqnarray}
\] となり，電源を流れる電流\( \ I_{0} \ \)は，
\[
\begin{eqnarray}
I_{0}&=&\frac {E}{R_{0}} \\[ 5pt ] &=&\frac {R_{2}+R_{3}}{R_{1}R_{2}+R_{2}R_{3}+R_{3}R_{1}}E \\[ 5pt ] \end{eqnarray}
\] となる。分流の法則より，\( \ I \ \)の大きさは，
\[
\begin{eqnarray}
I&=&\frac {R_{2}}{R_{2}+R_{3}}I_{0} \\[ 5pt ] &=&\frac {R_{2}}{R_{2}+R_{3}}\cdot \frac {R_{2}+R_{3}}{R_{1}R_{2}+R_{2}R_{3}+R_{3}R_{1}}E \\[ 5pt ] &=&\frac {R_{2}}{R_{1}R_{2}+R_{2}R_{3}+R_{3}R_{1}}E \\[ 5pt ] \end{eqnarray}
\] と求められる。

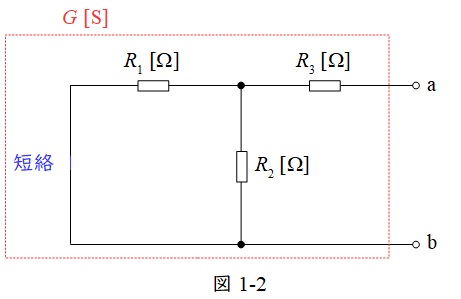
次に\( \ G \ \mathrm {[S]} \ \)について考える。問題文より，「コンダクタンス\( \ G \ \mathrm {[S]} \ \)の大きさは図1の直流電圧源を短絡し，端子\( \ \mathrm {a－b} \ \)からみたコンダクタンスの大きさに等しい」ので，題意に沿って図を描くと図1-2の通りとなる。図1-2における\( \ R_{1} \ \)と\( \ R_{2} \ \)の合成抵抗\( \ R_{12} \ \)は，ワンポイント解説「1.合成抵抗」より，
\[
\begin{eqnarray}
R_{12}&=&\frac {R_{1}R_{2}}{R_{1}+R_{2}} \\[ 5pt ] \end{eqnarray}
\] となり，\( \ R_{3} \ \)も含めた合成抵抗\( \ R_{0}^{\prime } \ \)は，
\[
\begin{eqnarray}
R_{0}^{\prime }&=&R_{12}+R_{3} \\[ 5pt ] &=&\frac {R_{1}R_{2}}{R_{1}+R_{2}}+R_{3} \\[ 5pt ] &=&\frac {R_{1}R_{2}+R_{2}R_{3}+R_{3}R_{1}}{R_{1}+R_{2}} \\[ 5pt ] \end{eqnarray}
\] となるので，コンダクタンス\( \ G \ \)は，
\[
\begin{eqnarray}
G&=&\frac {1}{R_{0}^{\prime }} \\[ 5pt ] &=&\frac {R_{1}+R_{2}}{R_{1}R_{2}+R_{2}R_{3}+R_{3}R_{1}} \\[ 5pt ] \end{eqnarray}
\] と求められる。