Contents
【問題】
【難易度】★★★★☆(やや難しい)
かごの質量が\( \ 250 \ \mathrm {kg} \ \),定格積載質量が\( \ 1500 \ \mathrm {kg} \ \)のロープ式エレベータにおいて,釣合いおもりの質量は,かごの質量に定格積載質量の\( \ 50 \ \mathrm {%} \ \)を加えた値とした。このエレベータの電動機出力を\( \ 22 \ \mathrm {kW} \ \)とした場合,一定速度でかごが上昇しているときの速度の値\( \ \mathrm {[m/min]} \ \)はいくらになるか,最も近いものを次の(1)~(5)のうちから一つ選べ。ただし,エレベータの機械効率は\( \ 70 \ \mathrm {%} \ \),積載量は定格積載質量とし,ロープの質量は無視するものとする。
(1) \(54\) (2) \(94\) (3) \(126\) (4) \(180\) (5) \(377\)
【ワンポイント解説】
エレベータの巻上げに必要な動力に関する問題で,半分は機械屋の問題です。しかし,電気をやっている以上,機械とのバランス計算は必ず必要となるので,電気を専門としていくならば機械の知識も習得する必要があります。主な電験のテキストだと,公式が書いてあるだけの場合が多いですが,きちんとメカニズムを理解した方が忘れにくく応用もききやすくなります。
1.動力\( \ P \ \)と力\( \ F \ \)の関係
ある物体を力\( \ F \ \mathrm {[N]} \ \),速度\( \ v \ \mathrm {[m/s]} \ \)で引っ張った時に必要な動力\( \ P \ \mathrm {[W]} \ \)との関係は,
\[
\begin{eqnarray}
P &=&Fv \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
解答:(3)
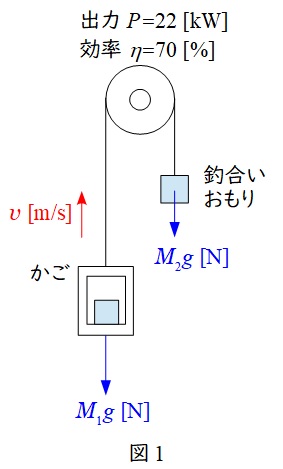
題意を図に示すと図1のようになる。(正確にはエレベータと滑車は異なりますが計算上は違いがないため滑車としています。)
図1においてかごにかかる力の大きさ\( \ F_{1} \ \)は,
\[
\begin{eqnarray}
F_{1} &=&M_{1}\mathrm {g} \\[ 5pt ]
&=&\left( 250+1500\right) \times 9.8 \\[ 5pt ]
&=&17150 \ \mathrm {[N]} \\[ 5pt ]
\end{eqnarray}
\]
となる。一方,釣合いおもりの質量\( \ M_{2} \ \)がかごの質量に定格積載質量の\( \ 50 \ \mathrm {%} \ \)すなわち\( \ 750 \ \mathrm {kg} \ \)を加えた値としたことから,
\[
\begin{eqnarray}
M_{2} &=&250+1500 \times 0.5 \\[ 5pt ]
&=&1000 \ \mathrm {[kg]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,釣合いおもりにかかる力の大きさ\( \ F_{2} \ \)は,
\[
\begin{eqnarray}
F_{2} &=&M_{2}\mathrm {g} \\[ 5pt ]
&=&1000 \times 9.8 \\[ 5pt ]
&=&9800 \ \mathrm {[N]} \\[ 5pt ]
\end{eqnarray}
\]
となり,電動機が引っ張る力の大きさ\( \ F \ \)は,
\[
\begin{eqnarray}
F&=&F_{1}-F_{2} \\[ 5pt ]
&=&17150-9800 \\[ 5pt ]
&=&7350 \ \mathrm {[N]} \\[ 5pt ]
\end{eqnarray}
\]
となる。また,エレベータの機械効率が\( \ 70 \ \mathrm {%} \ \)であることから,エレベータの動力\( \ P \ \)は,
\[
\begin{eqnarray}
P&=&22\times 10^{3}\times 0.70 \\[ 5pt ]
&=&15400 \ \mathrm {[W]} \\[ 5pt ]
\end{eqnarray}
\]
となる。ワンポイント解説「1.動力\( \ P \ \)と力\( \ F \ \)の関係」より,エレベータの速度\( \ v \ \)を求めると,
\[
\begin{eqnarray}
P &=&Fv \\[ 5pt ]
15400 &=&7350v \\[ 5pt ]
v&≒&2.095 \ \mathrm {[m/s]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ 1 \ \)分間あたり,
\[
\begin{eqnarray}
v&=&2.095\times 60 \\[ 5pt ]
&=&125.7 → 126 \ \mathrm {[m/min]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは