Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
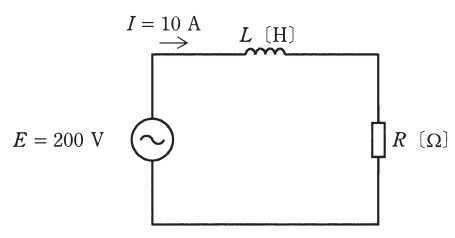
図のように,正弦波交流電圧\( \ E=200 \ \mathrm {[V]} \ \)の電源がインダクタンス\( \ L \ \mathrm {[H]} \ \)のコイルと\( \ R \ \mathrm {[\Omega ]} \ \)の抵抗との直列回路に電力を供給している。回路を流れる電流が\( \ I=10 \ \mathrm {[A]} \ \),回路の無効電力が\( \ Q=1200 \ \mathrm {[var]} \ \)のとき,抵抗\( \ R \ \mathrm {[\Omega ]} \ \)の値として,正しいものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 4 \ \) (2) \( \ 8 \ \) (3) \( \ 12 \ \) (4) \( \ 16 \ \) (5) \( \ 20 \ \)
【ワンポイント解説】
交流で直列の問題なので,まずベクトル図を描くことが重要となります。電圧と電流でベクトル図を描いても解けそうですが,無効電力が与えられていて,電源の電圧と電流が与えられているので,電力のベクトル図を描く方がより速く解けると思います。
1.皮相電力,有効電力,無効電力
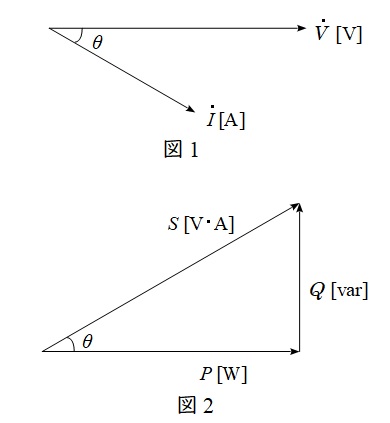
図1のような電圧\( \ V \ \),電流\( \ I \ \),電圧と電流の位相差が\( \ \theta \ \)(電流が遅れ)のベクトル図が与えられている時,皮相電力\( \ S \ \),有効電力\( \ P \ \),無効電力\( \ Q \ \)は図2のように描くことができ,それぞれの大きさは,
\[
\begin{eqnarray}
S &=&VI \\[ 5pt ]
P &=&VI\cos \theta \\[ 5pt ]
Q &=&VI\sin \theta \\[ 5pt ]
\end{eqnarray}
\]
となります。また,\( \ \cos \theta \ \)を力率と呼びます。
また,回路の抵抗が\( \ R \ \),リアクタンスが\( \ X \ \)であるとき,
\[
\begin{eqnarray}
P &=&RI^{2} \\[ 5pt ]
Q &=&XI^{2} \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。
【解答】
解答:(4)
電源の電圧\( \ E=200 \ \mathrm {[V]} \ \),回路を流れる電流\( \ I=10 \ \mathrm {[A]} \ \)なので,皮相電力\( \ S \ \)は,
\[
\begin{eqnarray}
S &=&EI \\[ 5pt ]
&=&200\times 10 \\[ 5pt ]
&=&2000 \ \mathrm {[V\cdot A]} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,電力のベクトル図は図3のように描け,有効電力\( \ P \ \)の大きさは,
\[
\begin{eqnarray}
P &=&\sqrt {S^{2}-Q^{2}} \\[ 5pt ]
&=&\sqrt {2000^{2}-1200^{2}} \\[ 5pt ]
&=&1600 \ \mathrm {[W]} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,抵抗\( \ R \ \)の大きさは,
\[
\begin{eqnarray}
R &=&\frac {P}{I^{2}} \\[ 5pt ]
&=&\frac {1600}{10^{2}} \\[ 5pt ]
&=&16 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
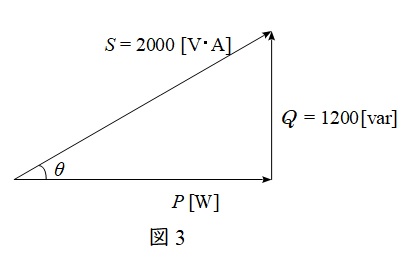






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは