《理論》〈電気回路〉[H24:問7]RLC直列共振回路の特性に関する空欄穴埋問題

Contents

1 【問題】
2 【ワンポイント解説】
- 2.1 【関連する「電気の神髄」記事】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，\( \ RLC \ \)直列共振回路に関する記述である。

\( \ R \ \mathrm {[\Omega ]} \ \)の抵抗，インダクタンス\( \ L \ \mathrm {[H]} \ \)のコイル，静電容量\( \ C \ \mathrm {[F]} \ \)のコンデンサを直列に接続した回路がある。

この回路に交流電圧を加え，その周波数を変化させると，特定の周波数\( \ f_{\mathrm {r}} \ \mathrm {[Hz]} \ \)のときに誘導性リアクタンス\( \ =2\pi f_{\mathrm {r}}L \ \mathrm {[\Omega ]} \ \)と容量性リアクタンス\( \ \displaystyle =\frac {1}{2\pi f_{\mathrm {r}}C} \ \mathrm {[\Omega ]} \ \)の大きさが等しくなり，その作用が互いに打ち消し合って回路のインピーダンスが\( \ \fbox {　（ア）　} \ \)なり，\( \ \fbox {　（イ）　} \ \)電流が流れるようになる。この現象を直列共振といい，このときの周波数\( \ f_{\mathrm {r}} \ \mathrm {[Hz]} \ \)をその回路の共振周波数という。

回路のリアクタンスは共振周波数\( \ f_{\mathrm {r}} \ \mathrm {[Hz]} \ \)より低い周波数では\( \ \fbox {　（ウ）　} \ \)となり，電圧より位相が\( \ \fbox {　（エ）　} \ \)電流が流れる。また，共振周波数\( \ f_{\mathrm {r}} \ \mathrm {[Hz]} \ \)より高い周波数では\( \ \fbox {　（オ）　} \ \)となり，電圧より位相が\( \ \fbox {　（カ）　} \ \)電流が流れる。

上記の記述中の空白箇所(ア)，(イ)，(ウ)，(エ)，(オ)及び(カ)に当てはまる組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。
\[
\begin{array}{ccccccc}
& （ア） & （イ） & （ウ） & （エ） & （オ） & （カ） \\
\hline
(1) & 大きく & 小さな & 容量性 & 進んだ & 誘導性 & 遅れた \\
\hline
(2) & 小さく & 大きな & 誘導性 & 遅れた & 容量性 & 進んだ \\
\hline
(3) & 小さく & 大きな & 容量性 & 進んだ & 誘導性 & 遅れた \\
\hline
(4) & 大きく & 小さな & 誘導性 & 遅れた & 容量性 & 進んだ \\
\hline
(5) & 小さく & 大きな & 容量性 & 遅れた & 誘導性 & 進んだ \\
\hline
\end{array}
\]

【ワンポイント解説】

共振周波数は非常によく出題される内容です。ただ単に共振周波数の公式を覚えているのではなく，どうしてそうなるのかを理解しておきましょう。

1.直列回路の共振回路
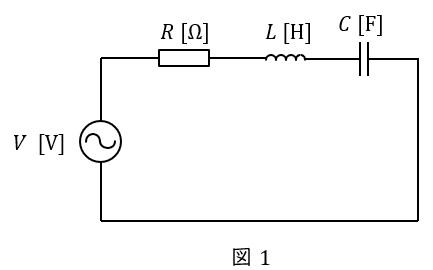
図1のような\( \ RLC \ \)直列回路があった場合の合成インピーダンス\( \ \dot Z \ \)は，角周波数を\( \ \omega \ \)とすると，
\[
\begin{eqnarray}
\dot Z&=&R+\mathrm {j}\omega L +\frac {1}{\mathrm {j}\omega C} \\[ 5pt ] &=&R+\mathrm {j}\left( \omega L -\frac {1}{\omega C}\right) \\[ 5pt ] \end{eqnarray}
\] となり，インピーダンスが最も小さくなるためには，上式の虚数部が零である必要があります。よって，共振角周波数\( \ \omega _{\mathrm {c}} \ \)は，
\[
\begin{eqnarray}
\omega_{\mathrm {c}} L -\frac {1}{\omega_{\mathrm {c}} C}&=&0 \\[ 5pt ] \omega_{\mathrm {c}} L &=&\frac {1}{\omega_{\mathrm {c}} C} \\[ 5pt ] \omega_{\mathrm {c}}^{2} &=&\frac {1}{LC} \\[ 5pt ] \omega_{\mathrm {c}} &=& \frac {1}{\sqrt {LC}} \\[ 5pt ] \end{eqnarray}
\] となります。また，共振周波数を\( \ f_{\mathrm {c}} \ \)とすると，\( \ \omega _{\mathrm {c}}=2\pi f_{\mathrm {c}} \ \)より，
\[
\begin{eqnarray}
f_{\mathrm {c}} &=& \frac {1}{2\pi \sqrt {LC}} \\[ 5pt ] \end{eqnarray}
\] となります。

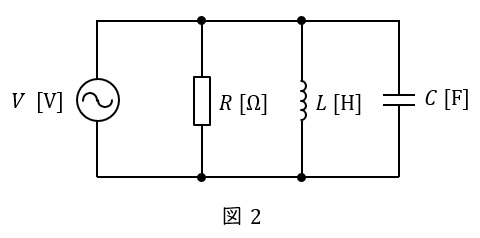
2.並列回路の共振回路
図2のような\( \ RLC \ \)並列回路があった場合の合成アドミタンス\( \ \dot Y \ \)は，角周波数を\( \ \omega \ \)とすると，
\[
\begin{eqnarray}
\dot Y&=&\frac {1}{R}+\mathrm {j}\omega C +\frac {1}{\mathrm {j}\omega L} \\[ 5pt ] &=&\frac {1}{R}+\mathrm {j}\left( \omega C -\frac {1}{\omega L}\right)
\end{eqnarray}
\] となり，アドミタンスが最も小さくなるためには，上式の虚数部が零である必要があります。よって，共振角周波数\( \ \omega _{\mathrm {c}} \ \)は，
\[
\begin{eqnarray}
\omega_{\mathrm {c}} C -\frac {1}{\omega_{\mathrm {c}} L}&=&0 \\[ 5pt ] \omega_{\mathrm {c}} C &=&\frac {1}{\omega_{\mathrm {c}} L} \\[ 5pt ] \omega_{\mathrm {c}}^{2} &=&\frac {1}{LC} \\[ 5pt ] \omega_{\mathrm {c}} &=& \frac {1}{\sqrt {LC}} \\[ 5pt ] \end{eqnarray}
\] となります。また，共振周波数を\( \ f_{\mathrm {c}} \ \)とすると，\( \ \omega _{\mathrm {c}}=2\pi f_{\mathrm {c}} \ \)より，
\[
\begin{eqnarray}
f_{\mathrm {c}} &=& \frac {1}{2\pi \sqrt {LC}} \\[ 5pt ] \end{eqnarray}
\] となります。

【関連する「電気の神髄」記事】

　　直列共振回路の理論

【解答】

解答：(3)
(ア)
ワンポイント解説「1.直列回路の共振回路」の通り，直列共振状態においては回路のインピーダンスは小さくなります。

(イ)
回路のインピーダンスは小さくなると，当然大きな電流が流れるようになります。その値は図1において，
\[
\begin{eqnarray}
I&=&\frac {V}{R} \\[ 5pt ] \end{eqnarray}
\] となります。

(ウ)
(エ)
ワンポイント解説「1.直列回路の共振回路」より，回路のインピーダンスは，
\[
\begin{eqnarray}
\dot Z&=&R+\mathrm {j}\left( 2\pi f L -\frac {1}{2\pi f C}\right)
\end{eqnarray}
\] で与えられ，共振周波数より低ければ\( \ \displaystyle \frac {1}{2\pi f C} ＞ 2\pi f L \ \)となり，この場合は電流の位相が電圧より進む容量性となります。

(オ)
(カ)
(ウ)，(エ)と同様に，共振周波数より高ければ\( \ \displaystyle 2\pi f L ＞ \frac {1}{2\pi f C} \ \)となり，この場合は電流の位相が電圧より遅れる誘導性となります。