【問題】
【難易度】★★★☆☆(普通)
極板\( \ \mathrm {A-B} \ \)間が誘電率\( \ \varepsilon _{0} \ \mathrm {[F/m]} \ \)の空気で満たされている平行平板コンデンサの空気ギャップ長を\( \ d \ \mathrm {[m]} \ \),静電容量を\( \ C_{0} \ \mathrm {[F]} \ \)とし,極板間の直流電圧を\( \ V_{0} \ \mathrm {[V]} \ \)とする。極板と同じ形状と面積を持ち,厚さが\( \ \displaystyle \frac {d}{4} \ \mathrm {[m]} \ \),誘電率\( \ \varepsilon _{1} \ \mathrm {[F/m]} \ \)の固体誘電体\( \ \left( \varepsilon _{1}>\varepsilon _{0}\right) \ \)を図に示す位置\( \ \mathrm {P-Q} \ \)間に極板と平行に挿入すると,コンデンサ内の電位分布は変化し,静電容量は\( \ C_{1} \ \mathrm {[F]} \ \)に変化した。このとき,誤っているものを次の(1)~(5)のうちから一つ選べ。
ただし,空気の誘電率を\( \ \varepsilon _{0} \ \),コンデンサの端効果は無視できるものとし,直流電圧\( \ V_{0} \ \mathrm {[V]} \ \)は一定とする。
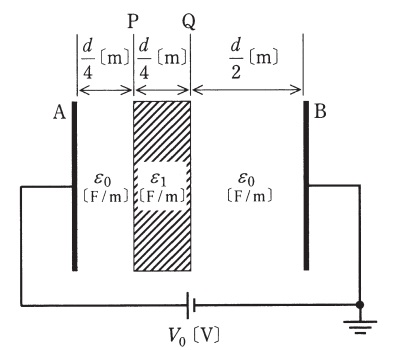
(1) 位置\( \ \mathrm {P} \ \)の電位は,固体誘電体を挿入する前の値よりも低下する。
(2) 位置\( \ \mathrm {Q} \ \)の電位は,固体誘電体を挿入する前の値よりも上昇する。
(3) 静電容量\( \ C_{1} \ \mathrm {[F]} \ \)は,\( \ C_{0} \ \mathrm {[F]} \ \)よりも大きくなる。
(4) 固体誘電体を導体に変えた場合,位置\( \ \mathrm {P} \ \)の電位は固体誘電体又は導体を挿入する前の値よりも上昇する。
(5) 固体誘電体を導体に変えた場合の静電容量\( \ C_{2} \ \mathrm {[F]} \ \)は,\( \ C_{0} \ \mathrm {[F]} \ \)よりも大きくなる。
【ワンポイント解説】
本問のような問題において,一番ポイントとなるのは具体的に計算しすぎて時間をかけすぎないことです。固体誘電体を挿入前後の位置\( \ \mathrm {P} \ \)の電位を具体的に求める必要はなく,誘電体部も真空部も電束密度\( \ D \ \)は一定であるということを理解していれば,かなり時間を短縮して解くことが可能となると思います。
1.平行平板コンデンサの静電容量\( \ C \ \)
平行平板コンデンサの静電容量\( \ C \ \)は,真空の誘電率を\( \ \varepsilon _{0} \ \),極板の面積を\( \ S \ \),極板間の距離を\( \ d \ \)とすると,
\[
\begin{eqnarray}
C &=&\frac {\varepsilon _{0}S}{d} \\[ 5pt ]
\end{eqnarray}
\]
となります。平行平板コンデンサの間に誘電率\( \ \varepsilon _{1} \ \)の誘電体を挿入すると,
\[
\begin{eqnarray}
C &=&\frac {\varepsilon _{1}S}{d} \\[ 5pt ]
\end{eqnarray}
\]
となります。基本的には真空の場合と同じ公式です。
2.平行平板コンデンサの電界\( \ E \ \)と電圧\( \ V \ \)の関係
極板間の距離\( \ d \ \)の平行平板コンデンサに電圧\( \ V \ \)をかけると,極板間の電界\(E\)は,
\[
\begin{eqnarray}
E&=&\frac {V}{d} \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.平行平板コンデンサの電束密度\( \ D \ \)と電界\( \ E \ \)の関係
極板間の誘電率を\( \ \varepsilon \ \)とすると,電束密度\( \ D \ \)と電界\( \ E \ \)には,
\[
\begin{eqnarray}
D&=&\varepsilon E \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。
【関連する「電気の神髄」記事】
【解答】
解答:(4)
(1)正しい
誘電体挿入前のコンデンサ内の電界の大きさは\( \ \displaystyle \frac {V_{0}}{d} \ \)となり一定である。
誘電体挿入後のコンデンサ内の電束密度を\( \ D \ \)と置くと,真空部の電界\( \ E_{0} \ \)及び誘電体部の電界\( \ E_{1} \ \)はそれぞれ,
\[
\begin{eqnarray}
E_{0}&=&\frac {D}{\varepsilon _{0}} \\[ 5pt ]
E_{1}&=&\frac {D}{\varepsilon _{1}} \\[ 5pt ]
\end{eqnarray}
\]
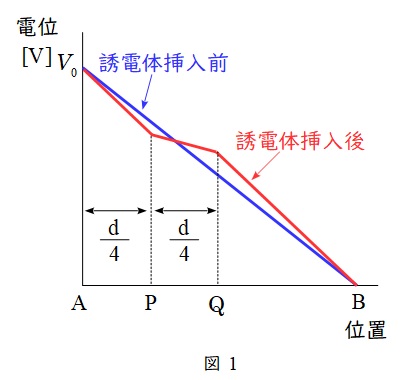
であり,\( \ \varepsilon _{1}>\varepsilon _{0} \ \)なので,\( \ E_{1}<E_{0} \ \)となる。\( \ V=Ed \ \)の関係から,誘電体挿入前後の電位の分布は図1のようなイメージとなる。したがって,位置\( \ \mathrm {P} \ \)の電位は,固体誘電体を挿入する前の値よりも低下する。
(2)正しい
図1の通り,位置\( \ \mathrm {Q} \ \)の電位は,固体誘電体を挿入する前の値よりも上昇する。
(3)正しい
誘電体挿入前の静電容量\( \ C_{0} \ \mathrm {[F]} \ \)は,
\[
\begin{eqnarray}
C_{0} &=&\frac {\varepsilon _{0}S}{d} \\[ 5pt ]
\end{eqnarray}
\]
となる。誘電体を全面に満たした場合の静電容量\( \ C_{\mathrm {f}} \ \mathrm {[F]} \ \)は,
\[
\begin{eqnarray}
C_{\mathrm {f}} &=&\frac {\varepsilon _{1}S}{d} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ C_{0}< C_{\mathrm {f}} \ \)となる。誘電体挿入後の静電容量\( \ C_{1} \ \mathrm {[F]} \ \)は,真空部が\( \ \displaystyle \frac {3d}{4} \ \mathrm {[m]} \ \),誘電体部が\( \ \displaystyle \frac {d}{4} \ \mathrm {[m]} \ \)であり,これは,全体を誘電体で満たした場合と真空の場合の中間的な性質を持つといえる。したがって,\( \ C_{0}<C_{1}< C_{\mathrm {f}} \ \)となる。
(4)誤り
導体に切り替えた場合,導体内の電位の低下がなくなる。したがって,図1の\( \ \mathrm {P-Q} \ \)間が水平になった場合と考えれば良い。したがって,位置\( \ \mathrm {P} \ \)の電位は,固体誘電体を挿入する前の値よりも低下する。
(5)正しい
導体に切り替えた場合の静電容量\( \ C_{2} \ \mathrm {[F]} \ \)は,極板間が\( \ \displaystyle \frac {3d}{4} \ \mathrm {[m]} \ \)となった静電容量と同じである。したがって,
\[
\begin{eqnarray}
C_{2} &=&\frac {\varepsilon _{0}S}{\displaystyle \frac {3d}{4}} \\[ 5pt ]
&=&\frac {4\varepsilon _{0}S}{3d} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ C_{0} \ \mathrm {[F]} \ \)よりも大きくなる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは