Contents
【問題】
【難易度】★★★☆☆(普通)
図のように,紙面に平行な平面内の平等電界\( \ E \ \mathrm {[V/m]} \ \)中で\( \ \mathrm {2 \ C} \ \)の点電荷を点\( \ \mathrm {A} \ \)から点\( \ \mathrm {B} \ \)まで移動させ,さらに点\( \ \mathrm {B} \ \)から点\( \ \mathrm {C} \ \)まで移動させた。この移動に,外力による仕事\( \ W=14 \ \mathrm {J} \ \)を要した。点\( \ \mathrm {A} \ \)の電位に対する点\( \ \mathrm {B} \ \)の電位\( \ V_{\mathrm {BA}} \ \mathrm {[V]} \ \)の値として,最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし,点電荷の移動はゆっくりであり,点電荷の移動によってこの平等電界は乱れないものとする。
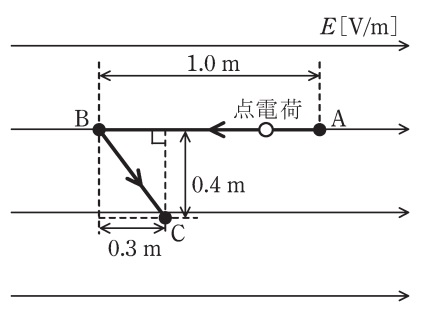
(1) \( \ 5 \ \) (2) \( \ 7 \ \) (3) \( \ 10 \ \) (4) \( \ 14 \ \) (5) \( \ 20 \ \)
【ワンポイント解説】
点電荷のエネルギーに関する問題です。一度解いてしまうとそれほど難解な公式を使用しないため理解はしやすいと思いますが,点\( \ \mathrm {B} \ \)から点\( \ \mathrm {C} \ \)までの移動等は電磁気の本質的な定義を理解していないと解けない問題かもしれません。
1.電界\( \ E \ \mathrm {[V/m]} \ \)と電位差\( \ V \ \mathrm {[V]} \ \)の関係
一様の電界\( \ E \ \mathrm {[V/m]} \ \)に逆らって,\( \ +1 \ \mathrm {C} \ \)の点電荷を移動する仕事が電位差\( \ V \ \mathrm {[V]} \ \)であり,点\( \ \mathrm {B} \ \)と点\( \ \mathrm {A} \ \)までの距離が\( \ d \ \mathrm {[m]} \ \)で電界が\( \ E \ \mathrm {[V/m]} \ \)であるとき,点\( \ \mathrm {A} \ \)と点\( \ \mathrm {B} \ \)の電位差\( \ V \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
V &=&Ed \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.電位差\( \ V \ \mathrm {[V]} \ \)と仕事\( \ W \ \mathrm {[J]} \ \)の関係
\( \ +Q\mathrm {[C]} \ \)の点電荷を電位差\( \ V \ \mathrm {[V]} \ \)移動させるための仕事\( \ W \ \mathrm {[J]} \ \)は,\( \ +1 \ \mathrm {C} \ \)の点電荷を移動する仕事が電位差\( \ V \ \mathrm {[V]} \ \)であるから,
\[
\begin{eqnarray}
W &=&QV \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
解答:(3)
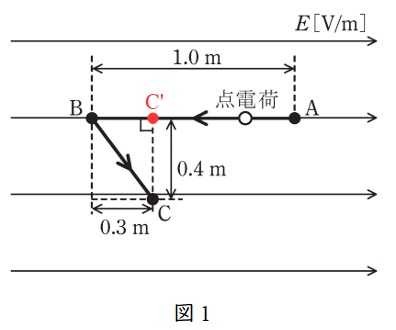
平等電界中においては,図1の通り点\( \ \mathrm {C} \ \)と点\( \ \mathrm {C}^{\prime } \ \)の電位は等しいので,点電荷を点\( \ \mathrm {A} \ \)から点\( \ \mathrm {C}^{\prime } \ \)まで移動させたエネルギーが外力による仕事\( \ W=14 \ \mathrm {[J]} \ \)となる。
本問における点電荷は\( \ Q=2 \ \mathrm {[C]} \ \)であるから,点\( \ \mathrm {A} \ \)と点\( \ \mathrm {C}^{\prime } \ \)の電位差\( \ V_{\mathrm {CA}} \ \mathrm {[V]} \ \)は,ワンポイント解説「2.電位差\( \ V \ \mathrm {[V]} \ \)と仕事\( \ W \ \mathrm {[J]} \ \)の関係」より,
\[
\begin{eqnarray}
W &=&QV_{\mathrm {CA}} \\[ 5pt ]
V_{\mathrm {CA}} &=&\frac {W}{Q} \\[ 5pt ]
&=&\frac {14}{2} \\[ 5pt ]
&=&7 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,平等電界\( \ E \ \mathrm {[V/m]} \ \)の大きさは,点\( \ \mathrm {A} \ \)から点\( \ \mathrm {C}^{\prime } \ \)までの距離\( \ d=1.0-0.3=0.7 \ \mathrm {[m]} \ \)であるから,ワンポイント解説「1.電界\( \ E \ \mathrm {[V/m]} \ \)と電位差\( \ V \ \mathrm {[V]} \ \)の関係」より,
\[
\begin{eqnarray}
V_{\mathrm {CA}} &=&Ed \\[ 5pt ]
E &=&\frac {V_{\mathrm {CA}}}{d} \\[ 5pt ]
&=&\frac {7}{0.7} \\[ 5pt ]
&=&10 \ \mathrm {[V/m]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,点\( \ \mathrm {A} \ \)の電位に対する点\( \ \mathrm {B} \ \)の電位\( \ V_{\mathrm {BA}} \ \mathrm {[V]} \ \)は,点\( \ \mathrm {A} \ \)から点\( \ \mathrm {B} \ \)までの距離\( \ d^{\prime }=1.0 \ \mathrm {[m]} \ \)であるから,
\[
\begin{eqnarray}
V_{\mathrm {BA}} &=&Ed^{\prime } \\[ 5pt ]
&=&10\times 1.0 \\[ 5pt ]
&=&10 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは