《理論》〈電気回路〉[H21:問7]不平衡負荷を接続した単相3線式回路の電流値の比較に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

図のように抵抗，コイル，コンデンサからなる負荷がある。この負荷に線間電圧\( \ {\dot V}_{\mathrm {ab}}= 100∠0° \ \mathrm {[V]} \ \)，\( \ {\dot V}_{\mathrm {bc}}= 100∠0° \ \mathrm {[V]} \ \)，\( \ {\dot V}_{\mathrm {ac}}= 200∠0° \ \mathrm {[V]} \ \)の単相\( \ 3 \ \)線式交流電源を接続したところ，端子\( \ \mathrm {a} \ \)，端子\( \ \mathrm {b} \ \)，端子\( \ \mathrm {c} \ \)を流れる線電流はそれぞれ\( \ {\dot I}_{\mathrm {a}} \ \mathrm {[A]} \ \)，\( \ {\dot I}_{\mathrm {b}} \ \mathrm {[A]} \ \)及び\( \ {\dot I}_{\mathrm {c}} \ \mathrm {[A]} \ \)であった。\( \ {\dot I}_{\mathrm {a}} \ \mathrm {[A]} \ \)，\( \ {\dot I}_{\mathrm {b}} \ \mathrm {[A]} \ \)，\( \ {\dot I}_{\mathrm {c}} \ \mathrm {[A]} \ \)の大きさをそれぞれ\( \ I_{\mathrm {a}} \ \mathrm {[A]} \ \)，\( \ I_{\mathrm {b}} \ \mathrm {[A]} \ \)，\( \ I_{\mathrm {c}} \ \mathrm {[A]} \ \)としたとき，これらの大小関係を表す式として，正しいのは次のうちどれか。

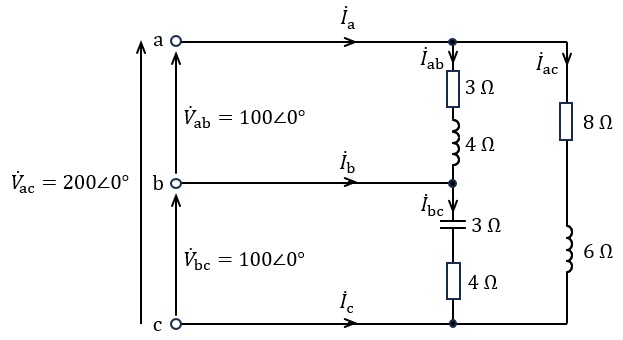
　(1)　\( \ I_{\mathrm {a}}=I_{\mathrm {c}}＞I_{\mathrm {b}} \ \)　　(2)　\( \ I_{\mathrm {a}}＞I_{\mathrm {c}}＞I_{\mathrm {b}} \ \)　　(3)　\( \ I_{\mathrm {b}}＞I_{\mathrm {c}}＞I_{\mathrm {a}} \ \)
　(4)　\( \ I_{\mathrm {b}}＞I_{\mathrm {a}}＞I_{\mathrm {c}} \ \)　　(5)　\( \ I_{\mathrm {c}}＞I_{\mathrm {a}}＞I_{\mathrm {b}} \ \)

【ワンポイント解説】

単相\( \ 3 \ \)線式線路に不平衡負荷を接続したときの線電流の比較に関する問題です。
やや計算量の多い問題となりますが，複素演算をできるだけ早く解けるように練習して下さい。

1.抵抗，コイル，コンデンサの電圧\( \ V \ \mathrm {[V]} \ \)と電流\( \ I \ \mathrm {[A]} \ \)の関係
抵抗\( \ R \ \mathrm {[\Omega ]} \ \)，コイル\( \ L \ \mathrm {[H]} \ \)，コンデンサ\( \ C \ \mathrm {[F]} \ \)があり，電源の角周波数\( \ \omega \ \mathrm {[rad / s]} \ \)及び周波数\( \ f \ \mathrm {[Hz]} \ \)が与えられているとき，それぞれのインピーダンスは，
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {R}}&=&R&& \\[ 5pt ] {\dot Z}_{\mathrm {L}}&=&\mathrm {j}\omega L&=&\mathrm {j}2\pi f L \\[ 5pt ] {\dot Z}_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C}&=&\frac {1}{\mathrm {j}2\pi f C} \\[ 5pt ] \end{eqnarray}
\] で求められ，それぞれの電圧と電流の関係は，
\[
\begin{eqnarray}
{\dot V}_{\mathrm {R}}&=&R\dot I \\[ 5pt ] {\dot V}_{\mathrm {L}}&=&\mathrm {j}\omega L \dot I \\[ 5pt ] {\dot V}_{\mathrm {C}}&=&\frac {\dot I }{\mathrm {j}\omega C} \\[ 5pt ] \end{eqnarray}
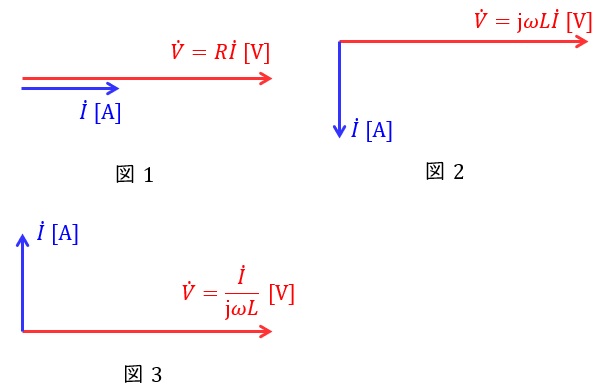
\] となります。この関係をベクトル図に表すと，図1～図3となります。

【解答】

解答：(2)
各相電流\( \ {\dot I}_{\mathrm {ab}} \ \mathrm {[A]} \ \)，\( \ {\dot I}_{\mathrm {bc}} \ \mathrm {[A]} \ \)，\( \ {\dot I}_{\mathrm {ac}} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {ab}}&=&\frac {{\dot V}_{\mathrm {ab}}}{3+\mathrm {j}4} \\[ 5pt ] &=&\frac {100}{3+\mathrm {j}4}\times \frac {3-\mathrm {j}4}{3-\mathrm {j}4} \\[ 5pt ] &=&\frac {100}{3^{2}+4^{2}}\left( 3-\mathrm {j}4\right) \\[ 5pt ] &=&12-\mathrm {j}16 \ \mathrm {[A]} \\[ 5pt ] {\dot I}_{\mathrm {bc}}&=&\frac {{\dot V}_{\mathrm {bc}}}{4-\mathrm {j}3} \\[ 5pt ] &=&\frac {100}{4-\mathrm {j}3}\times \frac {4+\mathrm {j}3}{4+\mathrm {j}3} \\[ 5pt ] &=&\frac {100}{4^{2}+3^{2}}\left( 4+\mathrm {j}3\right) \\[ 5pt ] &=&16+\mathrm {j}12 \ \mathrm {[A]} \\[ 5pt ] {\dot I}_{\mathrm {ac}}&=&\frac {{\dot V}_{\mathrm {ac}}}{8+\mathrm {j}6} \\[ 5pt ] &=&\frac {200}{8+\mathrm {j}6}\times \frac {8-\mathrm {j}6}{8-\mathrm {j}6} \\[ 5pt ] &=&\frac {200}{8^{2}+6^{2}}\left( 8-\mathrm {j}6\right) \\[ 5pt ] &=&16-\mathrm {j}12 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となるので，各線電流\( \ {\dot I}_{\mathrm {a}} \ \mathrm {[A]} \ \)，\( \ {\dot I}_{\mathrm {b}} \ \mathrm {[A]} \ \)，\( \ {\dot I}_{\mathrm {c}} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {a}}&=&{\dot I}_{\mathrm {ab}}+{\dot I}_{\mathrm {ac}} \\[ 5pt ] &=&\left( 12-\mathrm {j}16\right) +\left( 16-\mathrm {j}12\right) \\[ 5pt ] &=&28-\mathrm {j}28 \ \mathrm {[A]} \\[ 5pt ] {\dot I}_{\mathrm {b}}&=&{\dot I}_{\mathrm {bc}}-{\dot I}_{\mathrm {ab}} \\[ 5pt ] &=&\left( 16+\mathrm {j}12\right) -\left( 12-\mathrm {j}16\right) \\[ 5pt ] &=&4+\mathrm {j}28 \ \mathrm {[A]} \\[ 5pt ] {\dot I}_{\mathrm {c}}&=&-{\dot I}_{\mathrm {bc}}-{\dot I}_{\mathrm {ac}} \\[ 5pt ] &=&-\left( 16+\mathrm {j}12\right) -\left( 16-\mathrm {j}12\right) \\[ 5pt ] &=&-32 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，それぞれの大きさ\( \ I_{\mathrm {a}} \ \mathrm {[A]} \ \)，\( \ I_{\mathrm {b}} \ \mathrm {[A]} \ \)及び\( \ I_{\mathrm {c}} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {a}}&=&\sqrt {28^{2}+28^{2}} \\[ 5pt ] &≒&39.6 \ \mathrm {[A]} \\[ 5pt ] I_{\mathrm {b}}&=&\sqrt {4^{2}+28^{2}} \\[ 5pt ] &≒&28.3 \ \mathrm {[A]} \\[ 5pt ] I_{\mathrm {c}}&=&32 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となるので，\( \ I_{\mathrm {a}}＞I_{\mathrm {c}}＞I_{\mathrm {b}} \ \)と求められる。