《理論》〈電気回路〉[R2:問6]抵抗で消費される電力に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

図のように，三つの抵抗\( \ R_{\mathrm {1}}=3 \ \mathrm {\Omega } \ \)，\( \ R_{\mathrm {2}}=6 \ \mathrm {\Omega } \ \)，\( \ R_{\mathrm {3}}=2 \ \mathrm {\Omega } \ \)と電圧\( \ V \ \mathrm {[V]} \ \)の直流電源からなる回路がある。抵抗\( \ R_{\mathrm {1}} \ \)，\( \ R_{\mathrm {2}} \ \)，\( \ R_{\mathrm {3}} \ \)の消費電力をそれぞれ\( \ P_{\mathrm {1}} \ \mathrm {[W]} \ \)，\( \ P_{\mathrm {2}} \ \mathrm {[W]} \ \)，\( \ P_{\mathrm {3}} \ \mathrm {[W]} \ \)とするとき，その大きさの大きい順として，正しいものを次の(1)～(5)のうちから一つ選べ。

\[
\begin{eqnarray}
&(1)&　P_{\mathrm {1}} ＞ P_{\mathrm {2}} ＞ P_{\mathrm {3}}　　　　&(2)&　P_{\mathrm {1}} ＞ P_{\mathrm {3}} ＞ P_{\mathrm {2}}　　　　&(3)&　P_{\mathrm {2}} ＞ P_{\mathrm {1}} ＞ P_{\mathrm {3}} \\[ 5pt ] &(4)&　P_{\mathrm {2}} ＞ P_{\mathrm {3}} ＞ P_{\mathrm {1}}　　　　&(5)&　P_{\mathrm {3}} ＞ P_{\mathrm {1}} ＞ P_{\mathrm {2}}　　　　&&　\\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

直流回路の基本公式である分圧の法則と消費電力の公式が扱えるか問う問題です。電験の受験生であれば，かなり正答率が高い問題と予想されるので，確実に解けるようにしましょう。

1.合成抵抗
抵抗\( \ R_{1} \ \)と\( \ R_{2} \ \)が与えられている時，それぞれの合成抵抗\( \ R \ \)は以下の式で与えられます。

①直列
直列合成抵抗\( \ R \ \)は，
\[
\begin{eqnarray}
R&=&R_{1}+R_{2} \\[ 5pt ] \end{eqnarray}
\] となります。

②並列
並列合成抵抗\( \ R \ \)は，
\[
\begin{eqnarray}
\frac {1}{R}&=&\frac {1}{R_{1}}+\frac {1}{R_{2}} \\[ 5pt ] \end{eqnarray}
\] となり，整理すると，
\[
\begin{eqnarray}
R&=&\frac {R_{1}R_{2}}{R_{1}+R_{2}} \\[ 5pt ] \end{eqnarray}
\] となります。

2.分圧・分流の法則
①分圧の法則
図1に示した直列回路において，各抵抗にかかる電圧は以下の通りとなります。
\[
\begin{eqnarray}
V_{\mathrm {R1}}&=&\frac {R_{1}}{R_{1}+R_{2}}E \\[ 5pt ] V_{\mathrm {R2}}&=&\frac {R_{2}}{R_{1}+R_{2}}E \\[ 5pt ] \end{eqnarray}
\]

②分流の法則
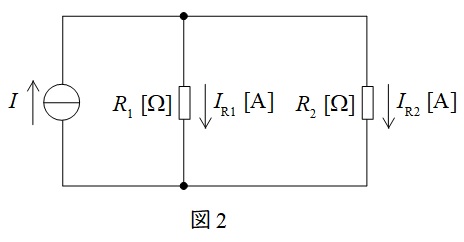
図2に示した並列回路において，各抵抗に流れる電流は以下の通りとなります。分子の抵抗が分圧の法則と逆となることに注意して下さい。
\[
\begin{eqnarray}
I_{\mathrm {R1}}&=&\frac {\color{red}{R_{2}}}{R_{1}+R_{2}}I \\[ 5pt ] I_{\mathrm {R2}}&=&\frac {\color{red}{R_{1}}}{R_{1}+R_{2}}I \\[ 5pt ] \end{eqnarray}
\]

3.抵抗での消費電力
抵抗値\( \ R \ \)の抵抗に電流\( \ I \ \)が流れているときの消費電力\( \ P \ \)は，
\[
\begin{eqnarray}
P &=&RI^{2} \\[ 5pt ] \end{eqnarray}
\] となり，オームの法則\( \ V=RI \ \)の関係から，
\[
\begin{eqnarray}
P &=&VI \\[ 5pt ] &=&\frac {V^{2}}{R} \\[ 5pt ] \end{eqnarray}
\] で求められます。

【解答】

解答：(2)
\( \ R_{\mathrm {2}} \ \)と\( \ R_{\mathrm {3}} \ \)の並列合成抵抗\( \ R_{\mathrm {23}} \ \)は，ワンポイント解説「1.合成抵抗」より，
\[
\begin{eqnarray}
R_{\mathrm {23}}&=&\frac {R_{2}R_{3}}{R_{2}+R_{3}} \\[ 5pt ] &=&\frac {6\times 2}{6+2} \\[ 5pt ] &=&1.5 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] であるから，それぞれの抵抗\( \ R_{\mathrm {1}} \ \)，\( \ R_{\mathrm {2}} \ \)，\( \ R_{\mathrm {3}} \ \)にかかる電圧\( \ V_{\mathrm {1}} \ \mathrm {[V]} \ \)，\( \ V_{\mathrm {2}} \ \mathrm {[V]} \ \)，\( \ V_{\mathrm {3}} \ \mathrm {[V]} \ \)は，分圧の法則より，
\[
\begin{eqnarray}
V_{\mathrm {1}}&=&\frac {R_{1}}{R_{1}+R_{23}}V \\[ 5pt ] &=&\frac {3}{3+1.5}\times V \\[ 5pt ] &≒&0.667 V \\[ 5pt ] V_{\mathrm {2}}&=&V_{\mathrm {3}}=\frac {R_{23}}{R_{1}+R_{23}}V \\[ 5pt ] &=&\frac {1.5}{3+1.5}\times V \\[ 5pt ] &≒&0.333 V \\[ 5pt ] \end{eqnarray}
\] となるので，それぞれの消費電力\( \ P_{\mathrm {1}} \ \mathrm {[W]} \ \)，\( \ P_{\mathrm {2}} \ \mathrm {[W]} \ \)，\( \ P_{\mathrm {3}} \ \mathrm {[W]} \ \)は，ワンポイント解説「3.抵抗での消費電力」より，
\[
\begin{eqnarray}
P_{\mathrm {1}}&=&\frac {V_{\mathrm {1}}^{2}}{R_{\mathrm {1}}} \\[ 5pt ] &=&\frac {\left( 0.667 V\right) ^{2}}{3} \\[ 5pt ] &≒&0.148 V^{2} \\[ 5pt ] P_{\mathrm {2}}&=&\frac {V_{\mathrm {2}}^{2}}{R_{\mathrm {2}}} \\[ 5pt ] &=&\frac {\left( 0.333 V\right) ^{2}}{6} \\[ 5pt ] &≒&0.0185 V^{2} \\[ 5pt ] P_{\mathrm {3}}&=&\frac {V_{\mathrm {3}}^{2}}{R_{\mathrm {3}}} \\[ 5pt ] &=&\frac {\left( 0.333 V\right) ^{2}}{2} \\[ 5pt ] &≒&0.0554 V^{2} \\[ 5pt ] \end{eqnarray}
\] となり，大きい順に並べると，\( \ P_{\mathrm {1}} ＞ P_{\mathrm {3}} ＞ P_{\mathrm {2}} \ \)と求められる。