《機械》〈電動機応用〉[R2:問11]はずみ車が減速する際に放出した平均出力に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

慣性モーメント\( \ 50 \ \mathrm {kg\cdot m^{2}} \ \)のはずみ車が，回転数\( \ 1 \ 500 \ \mathrm {{min}^{-1}} \ \)で回転している。このはずみ車に負荷が加わり，\( \ 2 \ \)秒間で\( \ 1 \ 000 \ \mathrm {{min}^{-1}} \ \)まで減速した。この間にはずみ車が放出した平均出力の値\( \ \mathrm {[kW]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。ただし，軸受の摩擦や空気の抵抗は無視できるものとする。

　(1)　\( \ 34 \ \)　　(2)　\( \ 137 \ \)　　(3)　\( \ 171 \ \)　　(4)　\( \ 308 \ \)　　(5)　\( \ 343 \ \)

【ワンポイント解説】

電動機応用のはずみ車に関する問題です。
慣性モーメントと運動エネルギーの関係式を知っていればそれほど難解な問題ではありませんが，運動エネルギーから最終的に平均出力を求める等の引っ掛けもあり，電気屋への出題としては少し難しめの問題となるかもしれません。

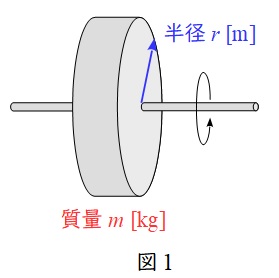
1.慣性モーメント\( \ J \ \)
質量\( \ m \ \mathrm {[kg]} \ \)，速度\( \ v \ \mathrm {[m/s]} \ \)で回転している回転体の運動エネルギー\( \ W \ \mathrm {[J]} \ \)は，
\[
\begin{eqnarray}
W &=& \frac {1}{2}mv^{2} \\[ 5pt ] \end{eqnarray}
\] であり，回転体の半径を\( \ r \ \mathrm {[m]} \ \)，角速度を\( \ \omega \ \mathrm {[rad/s]} \ \)とすると，\( \ v=r\omega \ \)の関係があるから，
\[
\begin{eqnarray}
W &=& \frac {1}{2}m\left( r\omega \right) ^{2} \\[ 5pt ] &=& \frac {1}{2}mr^{2}\omega ^{2} \\[ 5pt ] &=& \frac {1}{2}J\omega ^{2} \\[ 5pt ] \end{eqnarray}
\] となります。この\( \ J=mr ^{2} \ \)を慣性モーメントと呼びます。
慣性モーメントが大きいと，回転体は加速しにくく，減速しにくいという特徴があります。

【解答】

解答：(3)
回転速度\( \ N_{1}=1 \ 500 \ \mathrm {[{min}^{-1}]} \ \)及び\( \ N_{2}=1 \ 000 \ \mathrm {[{min}^{-1}]} \ \)の時の角速度\( \ \omega _{1} \ \mathrm {[rad/s]} \ \)及び\( \ \omega _{2} \ \mathrm {[rad/s]} \ \)は，
\[
\begin{eqnarray}
\omega _{1} &=& \frac {2\pi N_{1}}{60} \\[ 5pt ] &=& \frac {2\pi \times 1500}{60} \\[ 5pt ] &≒& 157.1 \ \mathrm {[rad/s]} \\[ 5pt ] \omega _{2} &=& \frac {2\pi N_{2}}{60} \\[ 5pt ] &=& \frac {2\pi \times 1000}{60} \\[ 5pt ] &≒& 104.7 \ \mathrm {[rad/s]} \\[ 5pt ] \end{eqnarray}
\] であるから，ワンポイント解説「1.慣性モーメント\( \ J \ \)」より，はずみ車が放出したエネルギー\( \ \Delta W \ \mathrm {[kJ]} \ \)は，慣性モーメント\( \ J=50 \ \mathrm {[kg\cdot m^{2}]} \ \)であるから，
\[
\begin{eqnarray}
\Delta W &=& \frac {1}{2}J\omega _{1} ^{2}-\frac {1}{2}J\omega _{2} ^{2} \\[ 5pt ] &=& \frac {1}{2}J\left( \omega _{1} ^{2}-\omega _{2} ^{2}\right) \\[ 5pt ] &=& \frac {1}{2}\times 50\times \left( 157.1 ^{2}-104.7 ^{2}\right) \\[ 5pt ] &≒& 343000 \ \mathrm {[J]}　→　343.0 \ \mathrm {[kJ]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，はずみ車が放出した平均出力（\( \ 1 \ \)秒間での放出エネルギー）\( \ P \ \mathrm {[kW]} \ \)は，
\[
\begin{eqnarray}
P &=& \frac {\Delta W}{2} \\[ 5pt ] &=& \frac {343.0}{2} \\[ 5pt ] &≒& 172 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。