【問題】
【難易度】★★☆☆☆(やや易しい)
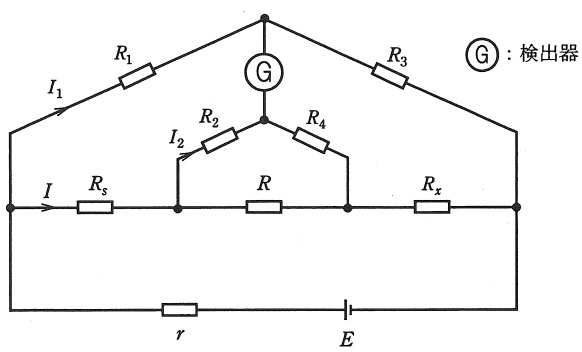
次の文章は,ケルビンダブルブリッジに関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる式を解答群の中から選び,その記号をマークシートに記入しなさい。
図において,\( \ R_{s} \ \)は既知の抵抗,\( \ R_{x} \ \)は未知の抵抗,\( \ R \ \)は\( \ R_{s} \ \)と\( \ R_{x} \ \)を接続する導体の抵抗,\( \ E \ \)は直流電源の電圧,\( \ r \ \)は電源の内部抵抗とし,Ⓖは検出器であるとする。いま,\( \ R_{1} \ \),\( \ R_{2} \ \),\( \ R_{3} \ \)及び\( \ R_{4} \ \)を適当な値に調整し,検出器Ⓖの指示が零となりブリッジが平衡したとすると,\( \ R_{1} \ \)と\( \ R_{3} \ \),\( \ R_{2} \ \)と\( \ R_{4} \ \)及び\( \ R_{s} \ \)と\( \ R_{x} \ \)に流れる電流はそれぞれ等しくなり,以下の式が成立する。ただし,各電流は矢印の方向に流れるものとする。
\[
\begin{eqnarray}
R_{1}I_{1} &=& \ \fbox { (1) } \ &・・・・・・・・・ ①& \\[ 5pt ]
R_{3}I_{1} &=& \ \fbox { (2) } \ &・・・・・・・・・ ②& \\[ 5pt ]
\end{eqnarray}
\]
また,\( \ I_{2} \ \)は,
\[
\begin{eqnarray}
I_{2} &=& \ \fbox { (3) } \ \times I &・・・・・・・・・ ③& \\[ 5pt ]
\end{eqnarray}
\]
したがって,①式~③式より,\( \ R_{x} \ \)は\( \ \fbox { (4) } \ \)となる。ここで,\( \ \displaystyle \frac {R_{3}}{R_{1}}=\frac {R_{4}}{R_{2}} \ \)となるように各抵抗を調整すれば,\( \ R_{x} \ \)は\( \ \fbox { (5) } \ \)となる。
〔問4の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {R_{3}}{R_{1}}R_{s} &(ロ)& \frac {R_{2}}{R_{3}}R_{s} \\[ 5pt ]
&(ハ)& \frac {R}{R_{2}+R_{4}+R} &(ニ)& R_{s}I+R_{2}I_{2} \\[ 5pt ]
&(ホ)& \frac {R_{2}}{R_{3}}R_{s}+\frac {R}{R_{2}+R_{4}}\left( \frac {R_{2}R_{3}}{R_{1}}-R_{4}\right) &(ヘ)& \frac {R_{1}}{R_{3}}R_{s} \\[ 5pt ]
&(ト)& \frac {R}{R_{2}} &(チ)& R_{x}I+R_{4}I_{2} \\[ 5pt ]
&(リ)& R_{s}I+\frac {R_{2}+R_{4}+R}{R}I_{2} &(ヌ)& R_{x}I+\frac {R_{2}+R_{4}+R}{R}I_{2} \\[ 5pt ]
&(ル)& \frac {R_{3}}{R_{1}}R_{s}+\frac {R}{R_{2}+R_{4}+R}\left( \frac {R_{2}R_{3}}{R_{1}}-R_{4}\right) &(ヲ)& \frac {R_{1}}{R_{3}}R_{s}+\frac {R}{R_{2}+R_{4}+R}\left( \frac {R_{2}R_{3}}{R_{1}}-R_{4}\right) \\[ 5pt ]
&(ワ)& R_{s}I+\frac {R_{2}}{R_{2}+R_{4}}I_{2} &(カ)& R_{x}I+\frac {R_{4}}{R_{2}+R_{4}}I_{2} \\[ 5pt ]
&(ヨ)& \frac {R}{R_{2}+R_{4}} && \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
ケルビンダブルブリッジを使用した未知の抵抗の導出に関する問題です。
ケルビンダブルブリッジはブリッジ回路としてはやや複雑な構成をしていますが,平衡条件の考え方としては他のブリッジ回路と変わりありません。
導体の抵抗等のホイートストンブリッジでは測定できない低抵抗を測定可能としたブリッジです。
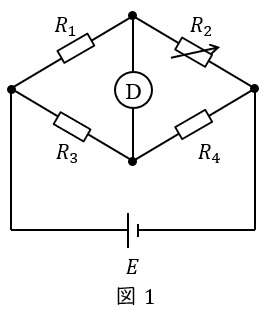
1.直流ブリッジ(ホイートストンブリッジ)の平衡条件
直流ブリッジ回路は抵抗の抵抗値を求める方法であり,図1のようなブリッジ回路をホイートストンブリッジと言います。
図1の回路において,検出器\( \ Ⓓ \ \)に電流が流れない条件を平衡条件と言い,
\[
\begin{eqnarray}
R_{1}R_{4} &=& R_{2}R_{3} \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。したがって,3つの既知の抵抗があれば,残りの1つの抵抗値を求めることができます。
【解答】
(1)解答:ニ
ブリッジが平衡しているとき,検出器Ⓖに電流が流れない,すなわち検出器Ⓖに繋がる端子間の電位差がないので,\( \ R_{1} \ \)での電圧降下と,\( \ R_{s} \ \)と\( \ R_{2} \ \)での電圧降下の合計値が等しい。したがって,
\[
\begin{eqnarray}
R_{1}I_{1} &=& R_{s}I+R_{2}I_{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:チ
(1)と同様に,ブリッジが平衡しているとき,\( \ R_{3} \ \)での電圧降下と,\( \ R_{4} \ \)と\( \ R_{x} \ \)での電圧降下の合計値が等しいので,
\[
\begin{eqnarray}
R_{3}I_{1} &=& R_{x}I+R_{4}I_{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ハ
検出器Ⓖには電流が流れないので,切り離して考えると,分流の法則より\( \ I_{2} \ \)は,
\[
\begin{eqnarray}
I_{2} &=&\frac {R}{R+\left( R_{2}+R_{4}\right) }I \\[ 5pt ]
&=&\frac {R}{R_{2}+R_{4}+R}I \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ル
(3)解答式を(1)及び(2)解答式に代入すると,
\[
\begin{eqnarray}
R_{1}I_{1} &=& R_{s}I+R_{2}\cdot \frac {R}{R_{2}+R_{4}+R}I && \\[ 5pt ]
&=& \left( R_{s}+\frac {R_{2}R}{R_{2}+R_{4}+R}\right) I & ・・・・・・・・・ ④& \\[ 5pt ]
R_{3}I_{1} &=& R_{x}I+R_{4}\cdot \frac {R}{R_{2}+R_{4}+R}I && \\[ 5pt ]
&=& \left( R_{x}+\frac {R_{4}R}{R_{2}+R_{4}+R}\right) I & ・・・・・・・・・ ⑤& \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ ④÷⑤ \ \)より,
\[
\begin{eqnarray}
\frac {R_{1}I_{1}}{R_{3}I_{1}} &=& \frac {\displaystyle \left( R_{s}+\frac {R_{2}R}{R_{2}+R_{4}+R}\right) I}{\displaystyle \left( R_{x}+\frac {R_{4}R}{R_{2}+R_{4}+R}\right) I} \\[ 5pt ]
\frac {R_{1}}{R_{3}} &=& \frac {\displaystyle R_{s}+\frac {R_{2}R}{R_{2}+R_{4}+R}}{\displaystyle R_{x}+\frac {R_{4}R}{R_{2}+R_{4}+R}} \\[ 5pt ]
R_{x}+\frac {R_{4}R}{R_{2}+R_{4}+R} &=&\left( R_{s}+\frac {R_{2}R}{R_{2}+R_{4}+R}\right) \frac {R_{3}}{R_{1}} \\[ 5pt ]
&=&\frac {R_{3}}{R_{1}}R_{s}+\frac {R_{2}R_{3}R}{R_{1}\left( R_{2}+R_{4}+R\right) } \\[ 5pt ]
R_{x}&=&\frac {R_{3}}{R_{1}}R_{s}+\frac {R_{2}R_{3}R}{R_{1}\left( R_{2}+R_{4}+R\right) }-\frac {R_{4}R}{R_{2}+R_{4}+R} \\[ 5pt ]
&=&\frac {R_{3}}{R_{1}}R_{s}+\frac {R}{R_{2}+R_{4}+R}\left( \frac {R_{2}R_{3}}{R_{1}}-R_{4}\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:イ
\( \ \displaystyle \frac {R_{3}}{R_{1}}=\frac {R_{4}}{R_{2}} \ \)すなわち\( \ \displaystyle \frac {R_{2}R_{3}}{R_{1}}=R_{4} \ \)より,(4)解答式の第二項のカッコ内が零となるので,
\[
\begin{eqnarray}
R_{x}&=&\frac {R_{3}}{R_{1}}R_{s} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん