【問題】
【難易度】★★★☆☆(普通)
次の文章は,直流抵抗回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる数値を解答群の中から選び,その記号を記述用紙の解答欄に記入しなさい。
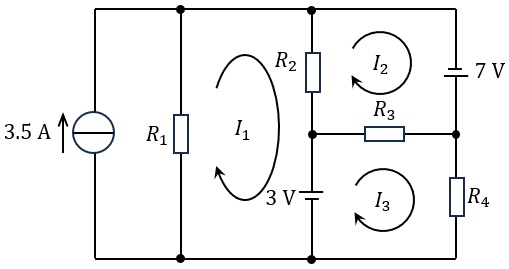
図のように,抵抗\( \ R_{1} \ \),\( \ R_{2} \ \),\( \ R_{3} \ \),\( \ R_{4} \ \)及び電圧源,電流源を接続した回路がある。図のように網目電流(閉路電流)\( \ I_{1} \ \),\( \ I_{2} \ \),\( \ I_{3} \ \)をとる。これらに関する方程式を求めると次式のようになった。
\[
\begin{eqnarray}
\begin{pmatrix}
6 & \ \fbox { (1) } \ & \ \fbox { (3) } \ \\
\ \fbox { (1) } \ & 5 & \ \fbox { (2) } \ \\
\ \fbox { (3) } \ & \ \fbox { (2) } \ & 4 \\
\end{pmatrix}\begin{pmatrix}
I_{1} \\[ 9pt ]
I_{2} \\[ 9pt ]
I_{3} \\[ 9pt ]
\end{pmatrix}=\begin{pmatrix}
4 \\[ 9pt ]
7 \\[ 9pt ]
3 \\[ 9pt ]
\end{pmatrix} \\[ 5pt ]
\end{eqnarray}
\]
このとき,電流\( \ I_{2} \ \)は\( \ \fbox { (4) } \ \mathrm {[A]} \ \),\( \ I_{3} \ \)は\( \ \fbox { (5) } \ \mathrm {[A]} \ \)となる。
〔問6の解答群〕
\[
\begin{eqnarray}
&(イ)& 4 &(ロ)& \frac {43}{25} &(ハ)& 3 \\[ 5pt ]
&(ニ)& 2 &(ホ)& \frac {139}{29} &(ヘ)& 0 \\[ 5pt ]
&(ト)& -2 &(チ)& -\frac {40}{7} &(リ)& -1 \\[ 5pt ]
&(ヌ)& -\frac {44}{29} &(ル)& 5 &(ヲ)& 1 \\[ 5pt ]
&(ワ)& \frac {5}{7} &(カ)& -4 &(ヨ)& \frac {8}{25} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
網目電流法を用いて,閉回路の網目電流を求める問題です。
本問のような,回路がやや複雑な回路計算においては,通常の枝電流法では仮定する電流が多くなるため,網目電流法を用いると効果的です。
また,問題では行列を用いた演算をしていますが,連立方程式を使用して解いても全く問題ありません。
計算力を必要とする問題ですが,ぜひこういう問題を得点できるように準備しましょう。
1.網目電流法
キルヒホッフの法則の一つで,閉回路に流れる網目電流に着目し,回路方程式を立てる方法です。
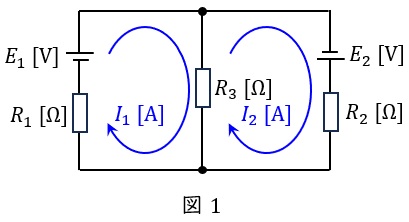
例えば図1の回路で,各網目電流を\( \ I_{1} \ \mathrm {[A]} \ \)及び\( \ I_{2} \ \mathrm {[A]} \ \)とおけば,回路方程式は,
\[
\begin{eqnarray}
E_{1}&=&R_{3}\left( I_{1}-I_{2}\right) +RI_{1} \\[ 5pt ]
E_{2}&=&R_{2}I_{2}+R_{3}\left( I_{2}-I_{1}\right) \\[ 5pt ]
\end{eqnarray}
\]
のように立てることができます。
2.逆行列の導出(掃出法)
\( \ 2\times 2 \ \)の行列では逆行列の公式がありますが,それ以上の行列では自分で計算して導出する必要があります。
\( \ \begin{pmatrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{pmatrix} \ \)の逆行列は,
\[
\begin{pmatrix}
a_{11} & a_{12} & a_{13} & 1 & 0 & 0 \\
a_{21} & a_{22} & a_{23} & 0 & 1 & 0 \\
a_{31} & a_{32} & a_{33} & 0 & 0 & 1
\end{pmatrix}
\]
と置いて,行の足し算引き算等を繰り返して,
\[
\begin{pmatrix}
1 & 0 & 0 & b_{11} & b_{12} & b_{13} \\
0 & 1 & 0 & b_{21} & b_{22} & b_{23} \\
0 & 0 & 1 & b_{31} & b_{32} & b_{33}
\end{pmatrix}
\]
のように変換した時の\( \
\begin{pmatrix}
b_{11} & b_{12} & b_{13} \\
b_{21} & b_{22} & b_{23} \\
b_{31} & b_{32} & b_{33}
\end{pmatrix}
\ \)
が逆行列となります。
【解答】
(1)解答:カ
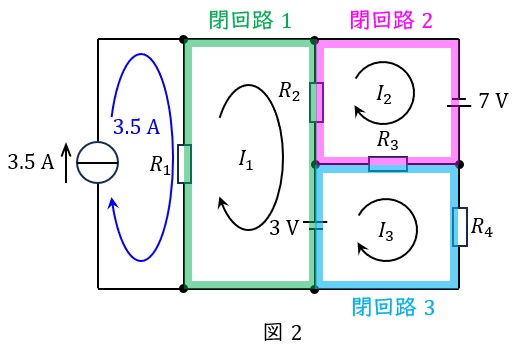
図2のように電流源による網目電流と閉回路\( \ 1 \ \)~\( \ 3 \ \)を設定する。
閉回路\( \ 1 \ \)について,回路方程式を立て整理すると,ワンポイント解説「1.網目電流法」の通り,
\[
\begin{eqnarray}
R_{1}\left( I_{1}-3.5\right) +R_{2}\left( I_{1}-I_{2}\right) +3&=&0 \\[ 5pt ]
R_{1} I_{1}-3.5R_{1} +R_{2}I_{1}-R_{2}I_{2} &=&-3 \\[ 5pt ]
\left( R_{1}+R_{2}\right) I_{1}-R_{2}I_{2} &=&3.5R_{1}-3 & \ ・・・・・・・・ ①& \\[ 5pt ]
\end{eqnarray}
\]
となり,同様に閉回路\( \ 2 \ \)について,回路方程式を立て整理すると,
\[
\begin{eqnarray}
R_{2}\left( I_{2}-I_{1}\right) +R_{3}\left( I_{2}-I_{3}\right) &=&7 \\[ 5pt ]
R_{2}I_{2}-R_{2}I_{1}+R_{3}I_{2}-R_{3}I_{3} &=&7 \\[ 5pt ]
-R_{2}I_{1}+\left( R_{2}+R_{3}\right)I_{2} -R_{3}I_{3} &=&7 &・・・・・・・・・・・・・・ ②& \\[ 5pt ]
\end{eqnarray}
\]
となり,さらに閉回路\( \ 3 \ \)について,回路方程式を立て整理すると,
\[
\begin{eqnarray}
R_{3}\left( I_{3}-I_{2}\right) +R_{4}I_{3} &=&3 \\[ 5pt ]
R_{3}I_{3}-R_{3}I_{2}+R_{4}I_{3} &=&3 \\[ 5pt ]
-R_{3}I_{2}+\left( R_{3}+R_{4}\right)I_{3} &=&3 &・・・・・・・・・・・・・・・・・・ ③& \\[ 5pt ]
\end{eqnarray}
\]
となる。①~③を行列で表すと,
\[
\begin{eqnarray}
\begin{pmatrix}
R_{1}+R_{2} & -R_{2} & 0 \\[ 5pt ]
-R_{2} & R_{2}+R_{3} & -R_{3} \\[ 5pt ]
0 & -R_{3} & R_{3}+R_{4} \\[ 5pt ]
\end{pmatrix}\begin{pmatrix}
I_{1} \\[ 5pt ]
I_{2} \\[ 5pt ]
I_{3} \\[ 5pt ]
\end{pmatrix}=\begin{pmatrix}
3.5R_{1}-3 \\[ 5pt ]
7 \\[ 5pt ]
3 \\[ 5pt ]
\end{pmatrix} \\[ 5pt ]
\end{eqnarray}
\]
となり,問題に与えられている行列と比較すると,
\[
\begin{eqnarray}
R_{1}+R_{2} &=&6 & \ ・・・・・・・・・・・・・・・・・・・・・・・・ ④& \\[ 5pt ]
R_{2}+R_{3} &=&5 & \ ・・・・・・・・・・・・・・・・・・・・・・・・ ⑤& \\[ 5pt ]
R_{3}+R_{4} &=&4 & \ ・・・・・・・・・・・・・・・・・・・・・・・・ ⑥& \\[ 5pt ]
3.5R_{1}-3 &=&4 & \ ・・・・・・・・・・・・・・・・・・・・・・・・ ⑦& \\[ 5pt ]
\end{eqnarray}
\]
となる。⑦より,
\[
\begin{eqnarray}
3.5R_{1}-3 &=&4 \\[ 5pt ]
3.5R_{1} &=&7 \\[ 5pt ]
R_{1} &=&2 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
となり,これを④~⑥に順次代入すれば,
\[
\begin{eqnarray}
R_{1}+R_{2} &=&6 \\[ 5pt ]
2+R_{2} &=&6 \\[ 5pt ]
R_{2} &=&4 \ \mathrm {[\Omega ]} \\[ 5pt ]
R_{2}+R_{3} &=&5 \\[ 5pt ]
4+R_{3} &=&5 \\[ 5pt ]
R_{3} &=&1 \ \mathrm {[\Omega ]} \\[ 5pt ]
R_{3}+R_{4} &=&4 \\[ 5pt ]
1+R_{4} &=&4 \\[ 5pt ]
R_{4} &=&3 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,(1)は\( \ -R_{2}=-4 \ \)と求められる。
(2)解答:リ
(1)と同様に(2)は\( \ -R_{3}=-1 \ \)と求められる。
(3)解答:ヘ
(1),(2)と同様に(3)は\( \ 0 \ \)と求められる。
(4)解答:ル
(1)~(3)より行列は,
\[
\begin{eqnarray}
\begin{pmatrix}
6 & -4 & 0 \\[ 5pt ]
-4 & 5 & -1 \\[ 5pt ]
0 & -1 & 4 \\[ 5pt ]
\end{pmatrix}\begin{pmatrix}
I_{1} \\[ 5pt ]
I_{2} \\[ 5pt ]
I_{3} \\[ 5pt ]
\end{pmatrix}=\begin{pmatrix}
4 \\[ 5pt ]
7 \\[ 5pt ]
3 \\[ 5pt ]
\end{pmatrix} \\[ 5pt ]
\end{eqnarray}
\]
となり,左から逆行列をかけると,
\[
\begin{eqnarray}
\begin{pmatrix}
6 & -4 & 0 \\[ 5pt ]
-4 & 5 & -1 \\[ 5pt ]
0 & -1 & 4 \\[ 5pt ]
\end{pmatrix}^{-1}\begin{pmatrix}
6 & -4 & 0 \\[ 5pt ]
-4 & 5 & -1 \\[ 5pt ]
0 & -1 & 4 \\[ 5pt ]
\end{pmatrix}\begin{pmatrix}
I_{1} \\[ 5pt ]
I_{2} \\[ 5pt ]
I_{3} \\[ 5pt ]
\end{pmatrix}=\begin{pmatrix}
6 & -4 & 0 \\[ 5pt ]
-4 & 5 & -1 \\[ 5pt ]
0 & -1 & 4 \\[ 5pt ]
\end{pmatrix}^{-1}\begin{pmatrix}
4 \\[ 5pt ]
7 \\[ 5pt ]
3 \\[ 5pt ]
\end{pmatrix} \\[ 5pt ]
\begin{pmatrix}
I_{1} \\[ 5pt ]
I_{2} \\[ 5pt ]
I_{3} \\[ 5pt ]
\end{pmatrix}=\begin{pmatrix}
6 & -4 & 0 \\[ 5pt ]
-4 & 5 & -1 \\[ 5pt ]
0 & -1 & 4 \\[ 5pt ]
\end{pmatrix}^{-1}\begin{pmatrix}
4 \\[ 5pt ]
7 \\[ 5pt ]
3 \\[ 5pt ]
\end{pmatrix} \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,\( \ \begin{pmatrix}
6 & -4 & 0 \\[ 5pt ]
-4 & 5 & -1 \\[ 5pt ]
0 & -1 & 4 \\[ 5pt ]
\end{pmatrix}^{-1} \ \)を求めるため,ワンポイント解説「2.逆行列の導出(掃出法)」の通り,\( \ \begin{pmatrix}
6 & -4 & 0 & 1 & 0 & 0 \\[ 5pt ]
-4 & 5 & -1 & 0 & 1 & 0 \\[ 5pt ]
0 & -1 & 4 & 0 & 0 & 1 \\[ 5pt ]
\end{pmatrix} \ \)とおき,\( \ 2 \ \)行目\( \times 4+3 \ \)行目を\( \ 2 \ \)行目にすれば,
\[
\begin{eqnarray}
\begin{pmatrix}
6 & -4 & 0 & 1 & 0 & 0 \\[ 5pt ]
-16 & 19 & 0 & 0 & 4 & 1 \\[ 5pt ]
0 & -1 & 4 & 0 & 0 & 1 \\[ 5pt ]
\end{pmatrix} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ 1 \ \)行目\( \times 8+2 \ \)行目\( \times 3 \ \)を\( \ 2 \ \)行目にすれば,
\[
\begin{eqnarray}
\begin{pmatrix}
6 & -4 & 0 & 1 & 0 & 0 \\[ 5pt ]
0 & 25 & 0 & 8 & 12 & 3 \\[ 5pt ]
0 & -1 & 4 & 0 & 0 & 1 \\[ 5pt ]
\end{pmatrix} \\[ 5pt ]
\begin{pmatrix}
6 & -4 & 0 & 1 & 0 & 0 \\[ 5pt ]
0 & 1 & 0 & \displaystyle \frac {8}{25} & \displaystyle \frac {12}{25} & \displaystyle \frac {3}{25} \\[ 5pt ]
0 & -1 & 4 & 0 & 0 & 1 \\[ 5pt ]
\end{pmatrix} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ 1 \ \)行目\( \ +2 \ \)行目\(\times 4 \ \)を\( \ 1 \ \)行目にすれば,
\[
\begin{eqnarray}
\begin{pmatrix}
6 & 0 & 0 & \displaystyle \frac {57}{25} & \displaystyle \frac {48}{25} & \displaystyle \frac {12}{25} \\[ 5pt ]
0 & 1 & 0 & \displaystyle \frac {8}{25} & \displaystyle \frac {12}{25} & \displaystyle \frac {3}{25} \\[ 5pt ]
0 & -1 & 4 & 0 & 0 & 1 \\[ 5pt ]
\end{pmatrix} \\[ 5pt ]
\begin{pmatrix}
1 & 0 & 0 & \displaystyle \frac {19}{50} & \displaystyle \frac {8}{25} & \displaystyle \frac {2}{25} \\[ 5pt ]
0 & 1 & 0 & \displaystyle \frac {8}{25} & \displaystyle \frac {12}{25} & \displaystyle \frac {3}{25} \\[ 5pt ]
0 & -1 & 4 & 0 & 0 & 1 \\[ 5pt ]
\end{pmatrix} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ 2 \ \)行目\( + 3 \ \)行目を\( \ 3 \ \)行目にすれば,
\[
\begin{eqnarray}
\begin{pmatrix}
1 & 0 & 0 & \displaystyle \frac {19}{50} & \displaystyle \frac {8}{25} & \displaystyle \frac {2}{25} \\[ 5pt ]
0 & 1 & 0 & \displaystyle \frac {8}{25} & \displaystyle \frac {12}{25} & \displaystyle \frac {3}{25} \\[ 5pt ]
0 & 0 & 4 & \displaystyle \frac {8}{25} & \displaystyle \frac {12}{25} & \displaystyle \frac {28}{25} \\[ 5pt ]
\end{pmatrix} \\[ 5pt ]
\begin{pmatrix}
1 & 0 & 0 & \displaystyle \frac {19}{50} & \displaystyle \frac {8}{25} & \displaystyle \frac {2}{25} \\[ 5pt ]
0 & 1 & 0 & \displaystyle \frac {8}{25} & \displaystyle \frac {12}{25} & \displaystyle \frac {3}{25} \\[ 5pt ]
0 & 0 & 1 & \displaystyle \frac {2}{25} & \displaystyle \frac {3}{25} & \displaystyle \frac {7}{25} \\[ 5pt ]
\end{pmatrix} \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
\begin{pmatrix}
6 & -4 & 0 \\[ 5pt ]
-4 & 5 & -1 \\[ 5pt ]
0 & -1 & 4 \\[ 5pt ]
\end{pmatrix}^{-1}&=&
\begin{pmatrix}
\displaystyle \frac {19}{50} & \displaystyle \frac {8}{25} & \displaystyle \frac {2}{25} \\[ 5pt ]
\displaystyle \frac {8}{25} & \displaystyle \frac {12}{25} & \displaystyle \frac {3}{25} \\[ 5pt ]
\displaystyle \frac {2}{25} & \displaystyle \frac {3}{25} & \displaystyle \frac {7}{25} \\[ 5pt ]
\end{pmatrix} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,
\[
\begin{eqnarray}
\begin{pmatrix}
I_{1} \\[ 5pt ]
I_{2} \\[ 5pt ]
I_{3} \\[ 5pt ]
\end{pmatrix}&=&\begin{pmatrix}
6 & -4 & 0 \\[ 5pt ]
-4 & 5 & -1 \\[ 5pt ]
0 & -1 & 4 \\[ 5pt ]
\end{pmatrix}^{-1}\begin{pmatrix}
4 \\[ 5pt ]
7 \\[ 5pt ]
3 \\[ 5pt ]
\end{pmatrix} \\[ 5pt ]
&=&\begin{pmatrix}
\displaystyle \frac {19}{50} & \displaystyle \frac {8}{25} & \displaystyle \frac {2}{25} \\[ 5pt ]
\displaystyle \frac {8}{25} & \displaystyle \frac {12}{25} & \displaystyle \frac {3}{25} \\[ 5pt ]
\displaystyle \frac {2}{25} & \displaystyle \frac {3}{25} & \displaystyle \frac {7}{25} \\[ 5pt ]
\end{pmatrix}\begin{pmatrix}
4 \\[ 5pt ]
7 \\[ 5pt ]
3 \\[ 5pt ]
\end{pmatrix} \\[ 5pt ]
&=&\begin{pmatrix}
\displaystyle \frac {19}{50}\times 4+\frac {8}{25}\times 7+\frac {2}{25}\times 3 \\[ 5pt ]
\displaystyle \frac {8}{25}\times 4+\frac {12}{25}\times 7+\frac {3}{25}\times 3 \\[ 5pt ]
\displaystyle \frac {2}{25}\times 4+\frac {3}{25}\times 7+\frac {7}{25}\times 3 \\[ 5pt ]
\end{pmatrix} \\[ 5pt ]
&=&\begin{pmatrix}
4 \\[ 5pt ]
5 \\[ 5pt ]
2 \\[ 5pt ]
\end{pmatrix} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ I_{2}=5 \ \mathrm {[A]} \ \)と求められる。
※模範解答として問題に合わせて掃出法を使用していますが,連立方程式として解いても問題ありません。
(5)解答:ニ
(4)解答式より,\( \ I_{3}=2 \ \mathrm {[A]} \ \)と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん