《理論》〈電磁気〉[H22:問1]直線状の無限長導体に流れる電流が作る磁界に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

次の文章は，直線状の無限長導体に流れる電流が作る磁界に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる語句又は式を解答群の中から選びなさい。
\( \ xyz \ \)直角座標系において磁束密度\( \ \boldsymbol B = \left( B_{\mathrm {x}}，B_{\mathrm {y}}，B_{\mathrm {z}} \right) \ \)に対して，次の式を満足するベクトル\( \ \boldsymbol A = \left( A_{\mathrm {x}}，A_{\mathrm {y}}，A_{\mathrm {z}} \right) \ \)を，\( \ \boldsymbol B \ \)のベクトルポテンシャルという。
\[
\begin{eqnarray}
\boldsymbol B&=&\mathrm {rot} \boldsymbol A&=\left( \frac{ \partial A_{\mathrm {z}}}{ \partial y } -\frac{ \partial A_{\mathrm {y}}}{ \partial z } ，\frac{ \partial A_{\mathrm {x}}}{ \partial z } -\frac{ \partial A_{\mathrm {z}}}{ \partial x }，\frac{ \partial A_{\mathrm {y}}}{ \partial x } -\frac{ \partial A_{\mathrm {x}}}{ \partial y }\right) 　・・・　① \\[ 5pt ] \end{eqnarray}
\] 図に示すように，真空中において，\( \ z \ \)軸上の無限長導体を正方向に流れる電流\( \ I \ \)による点\( \ \mathrm {P} \ \)におけるベクトルポテンシャルを求めてみる。

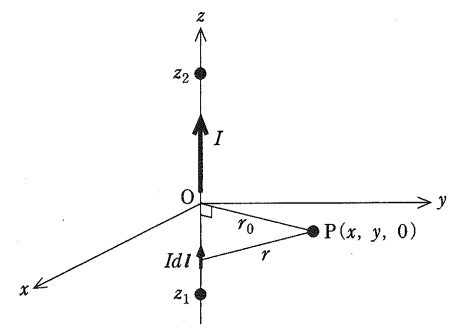
図中の電流素片\( \ Idl \ \)による点\( \ \mathrm {P}\left( x，y，0\right) \ \)における磁束密度\( \ d\boldsymbol B \ \)のベクトルポテンシャル\( \ d\boldsymbol A \ \)は，点\( \ \mathrm {P} \ \)の\( \ Idl \ \)からの距離を\( \ r \ \)として，次式で与えられる。ここで，\( \ \mu _{0} \ \)は真空の透磁率である。
\[
\begin{eqnarray}
d\boldsymbol A&=&\frac {\mu _{0}Idl}{4\pi r}　　・・・・・・・・・・・・・・・・・・・・・・・・・・　② \\[ 5pt ] \end{eqnarray}
\] 電流が\( \ z \ \)軸方向成分しか持たないことから，ベクトルポテンシャルは\( \ \fbox {　 （１） 　} \ \)方向成分だけを持つ。
点\( \ z_{1} \ \)から点\( \ z_{2} \ \)に流れる電流による，点\( \ \mathrm {P} \ \)におけるベクトルポテンシャルの\( \ \fbox {　 （１） 　} \ \)方向成分\( \ {A_{(1)成分　}}^{z_{1}z_{2}} \ \)は，②式から次式で表される。
\[
\begin{eqnarray}
{A_{(1)成分　}}^{z_{1}z_{2}}&=&\frac {\mu _{0}I}{4\pi }\int _{z_{1}}^{z_{2}} \ \fbox {　 （２） 　} \ \mathrm {d}z　　・・・・・・・・・・・・・・・　③ \\[ 5pt ] &=&\frac {\mu _{0}I}{4\pi }\ln \frac {z_{2}+\sqrt {x^{2}+y^{2}+z_{2}^{2}}}{z_{1}+\sqrt {x^{2}+y^{2}+z_{1}^{2}}}　 \ \ 　・・・・・・・・・・・　④ \\[ 5pt ] \end{eqnarray}
\] ここで，\( \ z_{1} → -\infty \ \)，\( \ z_{2} → +\infty \ \)とすると，ベクトルポテンシャルは発散してしまう。

そこで，\( \ z \ \)軸からの距離\( \ 1 \ \mathrm {[m]} \ \)の点のベクトルポテンシャルを基準として，点\( \ \mathrm {P} \ \)のベクトルポテンシャルを表すことを考える。すなわち，③式で表される任意の点のベクトルポテンシャルと，基準のベクトルポテンシャルとの差として新たにベクトルポテンシャルを表すことを考える。また，対称性を考慮して，\( \ -\infty \ \)から\( \ +\infty \ \)までの積分の代わりに\( \ 0 \ \)から\( \ +\infty \ \)までの積分値を\( \ 2 \ \)倍することで，次式を得る。
\[
\begin{eqnarray}
{A_{(1)成分　}}&=&2\times \frac {\mu _{0}I}{4\pi }\int _{0}^{\infty} \left( \ \fbox {　 （２） 　} \ – \ \fbox {　 （３） 　} \ \right) \mathrm {d}z　　・・・・・・・　⑤ \\[ 5pt ] \end{eqnarray}
\] この積分計算を行うと，\( \ {A_{(1)成分　}} \ \)は次式のように求めることができる。
\[
\begin{eqnarray}
{A_{(1)成分　}}&=&-\frac {\mu _{0}I}{4\pi }\ln \left( x^{2}+y^{2} \right)　 \ ・・・・・・・・・・・・・・・・・・・　⑥ \\[ 5pt ] \end{eqnarray}
\] これを①式に代入することで，点\( \ \mathrm {P} \ \)の磁束密度の各成分を求めることができる。例えば，磁束密度の\( \ x \ \)軸方向成分\( \ B_{\mathrm {x}} \ \)は次式のとおり求まる。
\[
\begin{eqnarray}
B_{\mathrm {x}}&=&-\frac {\mu _{0}I}{2\pi }\times \ \fbox {　 （４） 　} \ \ \ 　・・・・・・・・・・・・・・・・・・・・　⑦ \\[ 5pt ] \end{eqnarray}
\] 同様にして，\( \ B_{\mathrm {y}} \ \)，\( \ B_{\mathrm {z}} \ \)を求めることができ，これらより点\( \ \mathrm {P} \ \)における磁束密度\( \ \boldsymbol B \ \)の大きさは以下のように表すことができる。
\[
\begin{eqnarray}
B&=&\frac {\mu _{0}I}{2\pi }\times \ \fbox {　 （５） 　} \ 　・・・・・・・・・・・・・・・・・・・・・・　⑧ \\[ 5pt ] \end{eqnarray}
\]

〔問1の解答群〕
\[
\begin{eqnarray}
&（イ）&　\sqrt {x^{2}+y^{2}}　　　　　&（ロ）&　\frac {y}{x^{2}+y^{2}}　　　　　&（ハ）&　\frac {1}{z+\sqrt {x^{2}+y^{2}}} \\[ 5pt ] &（ニ）&　\frac {1}{x^{2}+y^{2}}　　　　　&（ホ）&　y \ 軸　　　　　&（ヘ）&　\sqrt {1+z^{2}} \\[ 5pt ] &（ト）&　\frac {y}{\sqrt {x^{2}+y^{2}}}　　　　　&（チ）&　z+\sqrt {x^{2}+y^{2}+z^{2}}　　　　　&（リ）&　\frac {1}{\sqrt {x^{2}+y^{2}+z^{2}}} \\[ 5pt ] &（ヌ）&　\frac {x}{x^{2}+y^{2}}　　　　　&（ル）&　\frac {1}{\sqrt {1+z^{2}}}　　　　　&（ヲ）&　z \ 軸 \\[ 5pt ] &（ワ）&　z+\sqrt {1+z^{2}}　　　　　&（カ）&　x \ 軸　　　　　&（ヨ）&　\frac {1}{\sqrt {x^{2}+y^{2}}} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

ベクトルポテンシャルを使用し電流と磁束密度の関係性を求める問題です。
\( \ \mathrm {rot} \ \)(回転)の公式も与えられており，微積分を使いこなせれば新たに必要な公式はありませんが，高い問題読解能力が必要とされる問題です。

【解答】

(1)解答：ヲ
題意より解答候補は，（ホ）\( \ y \ \)軸，（ヲ）\( \ z \ \)軸，（カ）\( \ x \ \)軸，になると思います。
②式において，\( \ Idl \ \)が\( \ z \ \)軸方向成分しか持たないため，ベクトルポテンシャル\( \ d\boldsymbol A \ \)も\( \ z \ \)軸方向成分だけを持つことになります。

(2)解答：リ
問題図において，任意の電流素片の点\( \ z \ \left( z_{1}≦z≦z_{2} \right) \ \)から点\( \ \mathrm {P}\left( x，y，0\right) \ \)までの距離\( \ r \ \)は，
\[
\begin{eqnarray}
r&=&\sqrt {x^{2}+y^{2}+z^{2}} \\[ 5pt ] \end{eqnarray}
\] となるので，②式は，
\[
\begin{eqnarray}
dA_{\mathrm {z}}&=&\frac {\mu _{0}I}{4\pi r}\mathrm {d}z \\[ 5pt ] &=&\frac {\mu _{0}I}{4\pi \sqrt {x^{2}+y^{2}+z^{2}}}\mathrm {d}z \\[ 5pt ] \end{eqnarray}
\] となる。これを両辺積分をとると，
\[
\begin{eqnarray}
A_{\mathrm {z}}^{z_{1}z_{2}}&=&\int _{z_{1}}^{z_{2}}\frac {\mu _{0}I}{4\pi \sqrt {x^{2}+y^{2}+z^{2}}}\mathrm {d}z \\[ 5pt ] &=&\frac {\mu _{0}I}{4\pi }\int _{z_{1}}^{z_{2}}\frac {1}{\sqrt {x^{2}+y^{2}+z^{2}}}\mathrm {d}z \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ル
\( \ z \ \)軸からの距離\( \ 1 \ \mathrm {[m]} \ \)の点のベクトルポテンシャルは\( \ x^{2}+y^{2}=1 \ \)とすれば良いので，⑤式は，
\[
\begin{eqnarray}
A_{\mathrm {z}}&=&2\times \frac {\mu _{0}I}{4\pi }\int _{0}^{\infty} \left( \frac {1}{\sqrt {x^{2}+y^{2}+z^{2}}} – \frac {1}{\sqrt {1+z^{2}}} \right) \mathrm {d}z \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ロ
⑥式を①式に代入して，磁束密度の\( \ x \ \)軸方向成分\( \ B_{\mathrm {x}} \ \)を求めると，\( \ A_{\mathrm {y}}=0 \ \)であるから，
\[
\begin{eqnarray}
B_{\mathrm {x}}&=&\frac{ \partial A_{\mathrm {z}}}{ \partial y } \\[ 5pt ] &=&\frac{ \partial }{ \partial y }\left\{ -\frac {\mu _{0}I}{4\pi }\ln \left( x^{2}+y^{2} \right) \right\} \\[ 5pt ] &=&-\frac {\mu _{0}I}{4\pi }\frac{ \partial }{ \partial y }\left\{ \ln \left( x^{2}+y^{2} \right) \right\} \\[ 5pt ] &=&-\frac {\mu _{0}I}{4\pi }\cdot 2y\cdot \frac {1}{x^{2}+y^{2}} \\[ 5pt ] &=&-\frac {\mu _{0}I}{2\pi }\cdot \frac {y}{x^{2}+y^{2}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ヨ
(4)と同様に，磁束密度の\( \ y \ \)軸方向成分\( \ B_{\mathrm {y}} \ \)，\( \ z \ \)軸方向成分\( \ B_{\mathrm {z}} \ \)は，\( \ A_{\mathrm {x}}=A_{\mathrm {y}}=0 \ \)であることに注意すると，
\[
\begin{eqnarray}
B_{\mathrm {y}}&=&\frac{ \partial A_{\mathrm {x}}}{ \partial z } -\frac{ \partial A_{\mathrm {z}}}{ \partial x } \\[ 5pt ] &=&-\frac{ \partial }{ \partial x }\left\{ -\frac {\mu _{0}I}{4\pi }\ln \left( x^{2}+y^{2} \right) \right\} \\[ 5pt ] &=&\frac {\mu _{0}I}{4\pi }\frac{ \partial }{ \partial x }\left\{ \ln \left( x^{2}+y^{2} \right) \right\} \\[ 5pt ] &=&\frac {\mu _{0}I}{4\pi }\cdot 2x\cdot \frac {1}{x^{2}+y^{2}} \\[ 5pt ] &=&\frac {\mu _{0}I}{2\pi }\cdot \frac {x}{x^{2}+y^{2}} \\[ 5pt ] B_{\mathrm {z}}&=&\frac{ \partial A_{\mathrm {y}}}{ \partial x } -\frac{ \partial A_{\mathrm {x}}}{ \partial y } \\[ 5pt ] &=&0 \\[ 5pt ] \end{eqnarray}
\] となるから，磁束密度\( \ \boldsymbol B \ \)の大きさは，
\[
\begin{eqnarray}
B&=&\sqrt {B_{\mathrm {x}}^{2}+B_{\mathrm {y}}^{2}+B_{\mathrm {z}}^{2}} \\[ 5pt ] &=&\sqrt {\left( -\frac {\mu _{0}I}{2\pi }\cdot \frac {y}{x^{2}+y^{2}}\right) ^{2}+\left( \frac {\mu _{0}I}{2\pi }\cdot \frac {x}{x^{2}+y^{2}}\right) ^{2}+0^{2}} \\[ 5pt ] &=&\frac {\mu _{0}I}{2\pi }\cdot \frac {1}{x^{2}+y^{2}}\sqrt {y ^{2}+x^{2}} \\[ 5pt ] &=&\frac {\mu _{0}I}{2\pi }\cdot \frac {1}{\sqrt {x^{2}+y^{2}}} \\[ 5pt ] \end{eqnarray}
\] と求められる。