【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,半導体\( \ \mathrm {PIN} \ \)ダイオードに関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
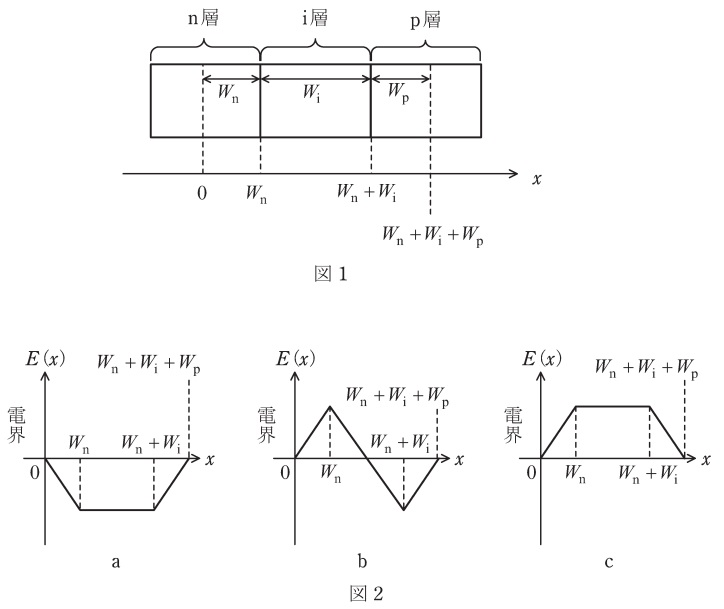
\( \ \mathrm {PIN} \ \)ダイオードは,図1のように,\( \ \mathrm {n} \ \)形半導体(\( \ \mathrm {n} \ \)層),真性半導体(\( \ \mathrm {i} \ \)層),\( \ \mathrm {p} \ \)形半導体(\( \ \mathrm {p} \ \)層)により構成される。半導体中のキャリヤ(電子と正孔)の拡散と再結合により,各層の境界付近には,キャリヤが存在しない空乏層が形成される。\( \ \mathrm {n} \ \)層の不純物濃度\( \ N_{\mathrm {D}} \ \)は場所によらず一定とし,全ての不純物が一価にイオン化していると仮定する。幅\( \ W_{\mathrm {n}} \ \)の空乏層の左端を\( \ x \ \)座標の原点とする\( \ 0≦x≦W_{\mathrm {n}} \ \)の領域の空間電荷密度\( \ \rho \ \)は,電気素量を\( \ e \left( >0\right) \ \)とすると,\( \ \rho = eN_{\mathrm {D}} \ \)となる。幅\( \ W_{\mathrm {i}} \ \)の真性半導体領域では\( \ \rho = 0 \ \)と仮定し,また,\( \ \mathrm {p} \ \)層の不純物濃度\( \ N_{\mathrm {A}} \ \)は一定とすると,幅\( \ W_{\mathrm {p}} \ \)の空乏層領域における空間電荷密度\( \ \rho \ \)は,\( \ \rho = \ \fbox { (1) } \ \)と表される。
ガウスの法則の一般式は,電界ベクトル\( \ \boldsymbol E \ \)を用いて次式のように表される。
\[
\begin{eqnarray}
\mathrm {div}\boldsymbol E&=&\frac {\rho }{\varepsilon } ・・・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
ただし,\( \ \varepsilon \ \)は誘電率である。電界ベクトル\( \ \boldsymbol E \ \)の\( \ x \ \)軸方向成分を,座標\( \ x \ \)の関数として表した\( \ E(x) \ \)を用いて,全空間電荷領域\( \ 0≦x≦W_{\mathrm {n}}+W_{\mathrm {i}}+W_{\mathrm {p}} \ \)の電界分布\( \ E(x) \ \)を求める。ここで,半導体の誘電率\( \ \varepsilon \ \)は\( \ \mathrm {n} \ \),\( \ \mathrm {i} \ \),\( \ \mathrm {p} \ \)層で同一とする。①式を\( \ 1 \ \)次元で表した微分方程式\( \ \displaystyle \fbox { (2) }=\frac {\rho }{\varepsilon } \ \)を解くと,\( \ \mathrm {n} \ \)層の空間電荷領域\( \ 0≦x≦W_{\mathrm {n}} \ \)における\( \ E(x) \ \)は,\( \ E(x)= \ \fbox { (3) } \ \)と表される。ただし,両端\( \ x=0 \ \)及び\( \ x=W_{\mathrm {n}}+W_{\mathrm {i}}+W_{\mathrm {p}} \ \)では,電界\( \ E(x)= 0 \ \)と仮定し,境界\( \ x=W_{\mathrm {n}} \ \)及び\( \ x=W_{\mathrm {n}}+W_{\mathrm {i}} \ \)では電界\( \ E(x) \ \)が連続となる条件を課すものとする。結果として,\( \ \mathrm {i} \ \)層の領域\( \ W_{\mathrm {n}}≦x≦W_{\mathrm {n}}+W_{\mathrm {i}} \ \)における\( \ E(x) \ \)は,\( \ E(x)= \ \fbox { (4) } \ \)と表される。全空間電荷領域における電界\( \ E(x) \ \)の概略は図2の\( \ \fbox { (5) } \ \)の図で示される。
\( \ \mathrm {PIN} \ \)ダイオードは,\( \ \mathrm {i} \ \)層による高電界の緩和や,高効率な光キャリヤ生成などの特徴を活かして,高耐圧整流器や高効率な光検出器,太陽電池などに幅広く応用されている。
〔問4の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {eN_{\mathrm {D}}}{\varepsilon }W_{\mathrm {i}} &(ロ)& \mathrm {c} &(ハ)& \frac {eN_{\mathrm {D}}}{\varepsilon }x \\[ 5pt ]
&(ニ)& \mathrm {a} &(ホ)& -\frac {eN_{\mathrm {D}}}{\varepsilon }x &(ヘ)& \frac {\mathrm {d}E\left( x\right) }{\mathrm {d}x} \\[ 5pt ]
&(ト)& \frac {eN_{\mathrm {D}}}{\varepsilon }x^{2} &(チ)& \frac {\mathrm {d}^{2}E\left( x\right) }{\mathrm {d}x^{2}} &(リ)& -eN_{\mathrm {A}} \\[ 5pt ]
&(ヌ)& -e\sqrt {N_{\mathrm {A}}N_{\mathrm {D}}} &(ル)& \frac {eN_{\mathrm {D}}}{\varepsilon }W_{\mathrm {n}} &(ヲ)& \mathrm {b} \\[ 5pt ]
&(ワ)& -\frac {\mathrm {d}E\left( x\right) }{\mathrm {d}x} &(カ)& eN_{\mathrm {A}} &(ヨ)& -\frac {eN_{\mathrm {D}}}{\varepsilon }W_{\mathrm {n}} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
\( \ \mathrm {PIN} \ \)ダイオードの特徴に関する問題ですが,ある程度電気の公式を理解している方であれば,問題文を読んで解けてしまうかもしれません。電験1種では本問のように知識と読解力を問うような問題も出題されます。
1.\( \ \mathrm {div} \ \)(発散)
ある微小な立方体の発散量で次式で定義されます。
\[
\begin{eqnarray}
\mathrm {div} \boldsymbol E &=& \frac { \partial E_{\mathrm {x}}}{ \partial x }+\frac { \partial E_{\mathrm {y}}}{ \partial y }+\frac { \partial E_{\mathrm {z}}}{ \partial z } \\[ 5pt ]
\end{eqnarray}
\]
【解答】
(1)解答:リ
幅\( \ W_{\mathrm {n}} \ \)の空乏層の左端を\( \ x \ \)座標の原点とする\( \ 0≦x≦W_{\mathrm {n}} \ \)の領域の空間電荷密度\( \ \rho \ \)は,電気素量を\( \ e \left( >0\right) \ \)とすると,\( \ \rho = eN_{\mathrm {D}} \ \)なので,これは\( \ \mathrm {n} \ \)層の領域の空間電荷密度を表している。
一方\( \ \mathrm {p} \ \)層では不純物濃度が\( \ N_{\mathrm {A}} \ \)なので,符号に注意すると,
\[
\begin{eqnarray}
\rho &=& -eN_{\mathrm {A}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ヘ
ワンポイント解説「1.\( \ \mathrm {div} \ \)(発散)」の通り,①式は,
\[
\begin{eqnarray}
\mathrm {div}\boldsymbol E&=&\frac {\rho }{\varepsilon } \\[ 5pt ]
\frac { \partial E_{\mathrm {x}}}{ \partial x }+\frac { \partial E_{\mathrm {y}}}{ \partial y }+\frac { \partial E_{\mathrm {z}}}{ \partial z }&=&\frac {\rho }{\varepsilon } \\[ 5pt ]
\frac { \mathrm {d} E_{\mathrm {x}}}{ \mathrm {d} x }+0+0&=&\frac {\rho }{\varepsilon } \\[ 5pt ]
\frac { \mathrm {d} E_{\mathrm {x}}}{\mathrm {d} x }&=&\frac {\rho }{\varepsilon } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ハ
(2)解答式を変数分離すると,
\[
\begin{eqnarray}
\frac { \mathrm {d} E_{\mathrm {x}}}{ \mathrm {d} x }&=&\frac {\rho }{\varepsilon } \\[ 5pt ]
\mathrm {d} E_{\mathrm {x}}&=&\frac {\rho }{\varepsilon }\mathrm {d} x \\[ 5pt ]
\end{eqnarray}
\]
となるので,両辺を積分すると,
\[
\begin{eqnarray}
E_{\mathrm {x}}&=&\frac {\rho }{\varepsilon } x+C ( Cは積分定数 ) \\[ 5pt ]
\end{eqnarray}
\]
となる。題意より\( \ x=0 \ \)の時\( \ E(x)= 0 \ \)なので,\( \ C=0 \ \)となり,
\[
\begin{eqnarray}
E_{\mathrm {x}}&=&\frac {\rho }{\varepsilon } x \\[ 5pt ]
&=&\frac {eN_{\mathrm {D}}}{\varepsilon }x \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ル
\( \ \mathrm {i} \ \)層すなわち\( \ W_{\mathrm {n}}≦x≦W_{\mathrm {n}}+W_{\mathrm {i}} \ \)において電界は連続であり,発散はないから,電界は一定となる。したがって,
\[
\begin{eqnarray}
E_{\mathrm {x}}&=&\frac {eN_{\mathrm {D}}}{\varepsilon } W_{\mathrm {n}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ロ
\( \ W_{\mathrm {n}}+W_{\mathrm {i}}≦x≦W_{\mathrm {n}}+W_{\mathrm {i}}+W_{\mathrm {p}} \ \)においては,(3)と同様に求めると,
\[
\begin{eqnarray}
E_{\mathrm {x}}&=&\frac {\rho }{\varepsilon } x+C ( Cは積分定数 ) \\[ 5pt ]
&=&\frac {-eN_{\mathrm {A}}}{\varepsilon }x +C ( Cは積分定数 )\\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ x=W_{\mathrm {n}}+W_{\mathrm {i}}+W_{\mathrm {p}} \ \)において,\( \ E(x)= 0 \ \)なので,
\[
\begin{eqnarray}
0&=&\frac {\rho }{\varepsilon } \left( W_{\mathrm {n}}+W_{\mathrm {i}}+W_{\mathrm {p}}\right) +C \\[ 5pt ]
C&=&-\frac {\rho }{\varepsilon } \left( W_{\mathrm {n}}+W_{\mathrm {i}}+W_{\mathrm {p}}\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,
\[
\begin{eqnarray}
E_{\mathrm {x}}&=&\frac {-eN_{\mathrm {A}}}{\varepsilon }x -\frac {\rho }{\varepsilon } \left( W_{\mathrm {n}}+W_{\mathrm {i}}+W_{\mathrm {p}}\right)\\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,上記式を満たすグラフは\( \ \mathrm { ( c ) } \ \)となる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん