【問題】
【難易度】★★★☆☆(普通)
次の文章は,交流回路の過渡現象に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
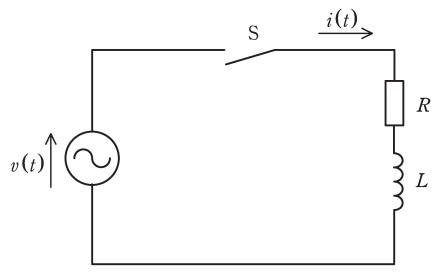
図の\( \ \mathrm {RL} \ \)回路において,時刻\( \ t<0 \ \)ではスイッチ\( \ \mathrm {S} \ \)は開いている。時刻\( \ t=0 \ \)でスイッチ\( \ \mathrm {S} \ \)を閉じ,回路に正弦波交流電圧\( \ v\left( t\right) =V_{\mathrm {m}}\sin \left( \omega t+\theta \right) \ \)が印加されるものとする。
回路の電流を\( \ i\left( t\right) \ \)とすれば,時刻\( \ t≧0 \ \)では次式の回路方程式が成立する。
\[
\begin{eqnarray}
\ \fbox { (1) } \ +Ri\left( t\right) &=& V_{\mathrm {m}}\sin \left( \omega t+\theta \right) ・・・・・・・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
時刻\( \ t≧0 \ \)における電流\( \ i\left( t\right) \ \)は,①式の定常解\( \ i_{\mathrm {s}}\left( t\right) \ \)と過渡解\( \ i_{\mathrm {T}}\left( t\right) \ \)の和として与えられる。
定常解\( \ i_{\mathrm {s}}\left( t\right) \ \)は,正弦波交流回路の定常電流として,
\[
\begin{eqnarray}
i_{\mathrm {s}}\left( t\right) &=& \frac {V_{\mathrm {m}}}{\sqrt {R^{2}+\left( \omega L\right) ^{2}}}\sin \left( \omega t+\theta -\phi \right) ・・・・・・・・・・・・・・ ② \\[ 5pt ]
\end{eqnarray}
\]
となる。ただし,\( \ \phi = \ \fbox { (2) } \ \)である。
一方,過渡解\( \ i_{\mathrm {T}}\left( t\right) \ \)は,①式の右辺を\( \ 0 \ \)とした場合の解であるので,任意定数を\( \ K \ \)とすれば次式となる。
\[
\begin{eqnarray}
i_{\mathrm {T}}\left( t\right) &=& K\times \ \fbox { (3) } ・・・・・・・・・・・・・・・・・・・・・・ ③ \\[ 5pt ]
\end{eqnarray}
\]
したがって,電流\( \ i\left( t\right) \ \)の一般解は,②式及び③式より,次式で与えられる。
\[
\begin{eqnarray}
i\left( t\right) &=& i_{\mathrm {s}}\left( t\right) + i_{\mathrm {T}}\left( t\right) =\frac {V_{\mathrm {m}}}{\sqrt {R^{2}+\left( \omega L\right) ^{2}}}\sin \left( \omega t+\theta -\phi \right) +K\times \ \fbox { (3) } ・・ ④ \\[ 5pt ]
\end{eqnarray}
\]
時刻\( \ t=0 \ \)における回路の電流\( \ i\left( 0\right) =0 \ \)であることに注意すれば,④式より任意定数\( \ K \ \)は次式で与えられる。
\[
\begin{eqnarray}
K &=& \ \fbox { (4) } ・・・・・・・・・・・・・・・・・・・・・・・・・・ ⑤ \\[ 5pt ]
\end{eqnarray}
\]
以上より,時刻\( \ t≧0 \ \)における回路の電流\( \ i\left( t\right) \ \)は,次式で与えらえる。
\[
\begin{eqnarray}
i\left( t\right) &=& \frac {V_{\mathrm {m}}}{\sqrt {R^{2}+\left( \omega L\right) ^{2}}}\sin \left( \omega t+\theta -\phi \right) + \ \fbox { (4) } \ \times \ \fbox { (3) } ・・ ⑥ \\[ 5pt ]
\end{eqnarray}
\]
なお,⑥式において\( \ \theta -\phi = \ \fbox { (5) } \ \)が成立する場合には,時刻\( \ t≧0 \ \)における電流\( \ i\left( t\right) \ \)は定常解\( \ i_{\mathrm {s}}\left( t\right) \ \)のみで表される。
〔問5の解答群〕
\[
\begin{eqnarray}
&(イ)& \tan ^{-1}\frac {1}{\omega LR} &(ロ)& \mathrm {e}^{-\frac {1}{RL}t} &(ハ)& 0 \\[ 5pt ]
&(ニ)& \tan ^{-1}\frac {\omega L}{R} &(ホ)& \mathrm {e}^{-\frac {R}{L}t} &(ヘ)& \omega Li\left( t\right) \\[ 5pt ]
&(ト)& \tan ^{-1}\frac {R}{\omega L} &(チ)& \frac {\mathrm {d}i\left( t\right) }{\mathrm {d}t} &(リ)& \frac {\pi }{4} \\[ 5pt ]
&(ヌ)& L\frac {\mathrm {d}i\left( t\right) }{\mathrm {d}t} &(ル)& \frac {\pi }{2} &(ヲ)& \mathrm {e}^{-\frac {L}{R}t} \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
&(ワ)& \frac {-V_{\mathrm {m}}}{\sqrt {R^{2}+\left( \omega L\right) ^{2}}}\sin \left( \theta -\phi \right) \\[ 5pt ]
&(カ)& \frac {V_{\mathrm {m}}}{\sqrt {R^{2}+\left( \omega L\right) ^{2}}}\sin \left( \theta -\phi \right) \\[ 5pt ]
&(ヨ)& \frac {V_{\mathrm {m}}}{\sqrt {R^{2}+\left( \omega L\right) ^{2}}}\sin \left( \theta +\phi \right) \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
交流回路の過渡現象に関する問題です。
過渡現象は直流回路がメインですが,交流回路においても考え方は同じです。
\( \ 2 \ \)種の際にも使用した交流回路の計算と過渡現象の知識を組み合わせて解くようにして下さい。
1.過渡現象における\( \ RLC \ \)それぞれの電圧
線路に流れる電流を\( \ i \ \)とし,抵抗\( \ R \ \)の電圧\( \ V_{\mathrm{R}} \ \),リアクトル\( \ L \ \)の電圧\( \ V_{\mathrm{L}} \ \),コンデンサ\( \ C \ \)の電圧\( \ V_{\mathrm{C}} \ \)とすると,
\[
\begin{eqnarray}
V_{\mathrm{R}} &=& Ri \\[ 5pt ]
V_{\mathrm{L}} &=& L\frac {\mathrm {d}i}{\mathrm {d}t} \\[ 5pt ]
V_{\mathrm{C}} &=& \frac {1}{C}\int i \mathrm {d}t =\frac {q}{C}\\[ 5pt ]
\end{eqnarray}
\]
となります。
2.過渡現象における定常解と過渡解
ⅰ.定常解を\( \ i_{\mathrm {s}} \ \),過渡解を\( \ i_{\mathrm {t}} \ \)とすると,電流値\( \ i \ \)は\( \ i=i_{\mathrm {s}}+i_{\mathrm {t}} \ \)となります。
ⅱ.定常解は電流の時間変化のない状態すなわち\( \ \displaystyle \frac {\mathrm {d}i_{\mathrm {s}}}{\mathrm {d}t}=0 \ \)とした時の解です。
ⅲ.過渡解はスイッチを入れた直後の解です。
3.自然対数の微分積分
①自然対数の微分
\[
\begin{eqnarray}
\frac {\mathrm {d}}{\mathrm {d}x} \left ( \ln {x} \right) &=&\frac {1}{x} \\[ 5pt ]
\end{eqnarray}
\]
②自然対数の積分
\[
\begin{eqnarray}
\int \frac {1}{x} \mathrm {d}x&=&\ln {x} + C \left( Cは積分定数\right) \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
\ln {x} &=&-\alpha t +C \left( Cは積分定数\right)の時, x=A\mathrm {e}^{-\alpha t} \left( A=\mathrm {e}^{C}\right)となります。 \\[ 5pt ]
\end{eqnarray}
\]
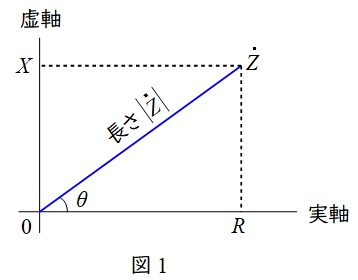
4.複素平面における複素数の表記方法
図1のような複素空間上の値\( \ \dot Z =R+\mathrm {j}X \ \)において,以下のような表記方法が定義されます。
ただし,\( \ \dot Z \ \)の絶対値\( \ \left| \dot Z\right| = \sqrt {R^{2}+X^{2}} \ \),\( \ \dot Z \ \)と実軸となす角を\( \ \theta \ \)とします。
①直交座標表記
\[
\begin{eqnarray}
\dot Z &=&\left| \dot Z\right| \left( \cos \theta +\mathrm {j}\sin \theta \right) \\[ 5pt ]
\end{eqnarray}
\]
②指数表記
\[
\begin{eqnarray}
\dot Z &=&\left| \dot Z\right| \mathrm {e}^{\mathrm {j}\theta } \\[ 5pt ]
\end{eqnarray}
\]
ただし,
\[
\begin{eqnarray}
\mathrm {e}^{\mathrm {j}\theta }&=&\cos \theta +\mathrm {j}\sin \theta \\[ 5pt ]
\end{eqnarray}
\]
であり,これをオイラーの公式といいます。
③極座標表記
\[
\begin{eqnarray}
\dot Z &=&\left| \dot Z\right| ∠\theta \\[ 5pt ]
\end{eqnarray}
\]
【解答】
(1)解答:ヌ
ワンポイント解説「1.過渡現象における\( \ RLC \ \)それぞれの電圧」の通り,問題図の回路における回路方程式は,
\[
\begin{eqnarray}
L\frac {\mathrm {d}i\left( t\right) }{\mathrm {d}t} +Ri\left( t\right) &=& V_{\mathrm {m}}\sin \left( \omega t+\theta \right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ニ
正弦波交流電圧\( \ v\left( t\right) \ \)のベクトル表記を\( \ \dot V \ \),定常解\( \ i_{\mathrm {s}}\left( t\right) \ \)のベクトル表記を\( \ {\dot I}_{\mathrm {s}} \ \)とすると,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {s}} &=& \frac {\dot V}{R+\mathrm {j}\omega L} \\[ 5pt ]
&=& \frac {\dot V}{R^{2}+\left( \omega L\right) ^{2}} \left( R-\mathrm {j}\omega L\right) \\[ 5pt ]
&=& \frac {\dot V}{\sqrt {R^{2}+\left( \omega L\right) ^{2}}} \left\{ \frac {R}{\sqrt {R^{2}+\left( \omega L\right) ^{2}}}-\mathrm {j}\frac {\omega L}{\sqrt {R^{2}+\left( \omega L\right) ^{2}}}\right\} \\[ 5pt ]
&=& \frac {\dot V}{\sqrt {R^{2}+\left( \omega L\right) ^{2}}} \left( \cos \phi -\mathrm {j}\sin \phi \right) \left( ただし,\phi =\tan ^{-1} \frac {\omega L}{R}\right) \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ {\dot I}_{\mathrm {s}} \ \)は\( \ \dot V \ \)より\( \ \phi \ \)だけ遅れることになる。これを瞬時値表記にすれば,
\[
\begin{eqnarray}
i_{\mathrm {s}}\left( t\right) &=& \frac {V_{\mathrm {m}}}{\sqrt {R^{2}+\left( \omega L\right) ^{2}}}\sin \left( \omega t+\theta -\phi \right) \left( ただし,\phi =\tan ^{-1} \frac {\omega L}{R}\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ホ
過渡解\( \ i_{\mathrm {T}}\left( t\right) \ \)は,①式の右辺を\( \ 0 \ \)とした場合の解であるので,
\[
\begin{eqnarray}
L\frac {\mathrm {d}i_{\mathrm {T}}\left( t\right) }{\mathrm {d}t} +Ri_{\mathrm {T}}\left( t\right) &=& 0 \\[ 5pt ]
L\frac {\mathrm {d}i_{\mathrm {T}}\left( t\right) }{\mathrm {d}t} &=& -Ri_{\mathrm {T}}\left( t\right) \\[ 5pt ]
\frac {1}{i_{\mathrm {T}}\left( t\right)}\mathrm {d}i_{\mathrm {T}}\left( t\right) &=& -\frac {R}{L}\mathrm {d}t \\[ 5pt ]
\end{eqnarray}
\]
となり,両辺積分すると,
\[
\begin{eqnarray}
\ln i_{\mathrm {T}}\left( t\right) &=& -\frac {R}{L}t+C \left( Cは積分定数\right) \\[ 5pt ]
i_{\mathrm {T}}\left( t\right) &=& K\mathrm {e}^{-\frac {R}{L}t} \left( K=\mathrm {e}^{C}\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ワ
④式の通り,一般解\( \ i\left( t\right) \ \)は,
\[
\begin{eqnarray}
i\left( t\right) &=& i_{\mathrm {s}}\left( t\right) + i_{\mathrm {T}}\left( t\right) \\[ 5pt ]
&=&\frac {V_{\mathrm {m}}}{\sqrt {R^{2}+\left( \omega L\right) ^{2}}}\sin \left( \omega t+\theta -\phi \right) +K\mathrm {e}^{-\frac {R}{L}t} \\[ 5pt ]
\end{eqnarray}
\]
となるので,初期条件\( \ i\left( 0\right) =0 \ \)より,
\[
\begin{eqnarray}
0 &=&\frac {V_{\mathrm {m}}}{\sqrt {R^{2}+\left( \omega L\right) ^{2}}}\sin \left( \omega \times 0+\theta -\phi \right) +K\mathrm {e}^{-\frac {R}{L}\times 0} \\[ 5pt ]
&=&\frac {V_{\mathrm {m}}}{\sqrt {R^{2}+\left( \omega L\right) ^{2}}}\sin \left( \theta -\phi \right) +K \\[ 5pt ]
K &=&-\frac {V_{\mathrm {m}}}{\sqrt {R^{2}+\left( \omega L\right) ^{2}}}\sin \left( \theta -\phi \right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ハ
時刻\( \ t≧0 \ \)における電流\( \ i\left( t\right) \ \)が定常解\( \ i_{\mathrm {s}}\left( t\right) \ \)のみで表されるとき,任意の時刻において過渡解が零である必要があるので,
\[
\begin{eqnarray}
-\frac {V_{\mathrm {m}}}{\sqrt {R^{2}+\left( \omega L\right) ^{2}}}\sin \left( \theta -\phi \right)\mathrm {e}^{-\frac {R}{L}t} &=& 0 \\[ 5pt ]
\sin \left( \theta -\phi \right) &=& 0 \\[ 5pt ]
\theta -\phi &=& 0 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん