【問題】
【難易度】★★★☆☆(普通)
次の文章は,エミッタ接地増幅回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
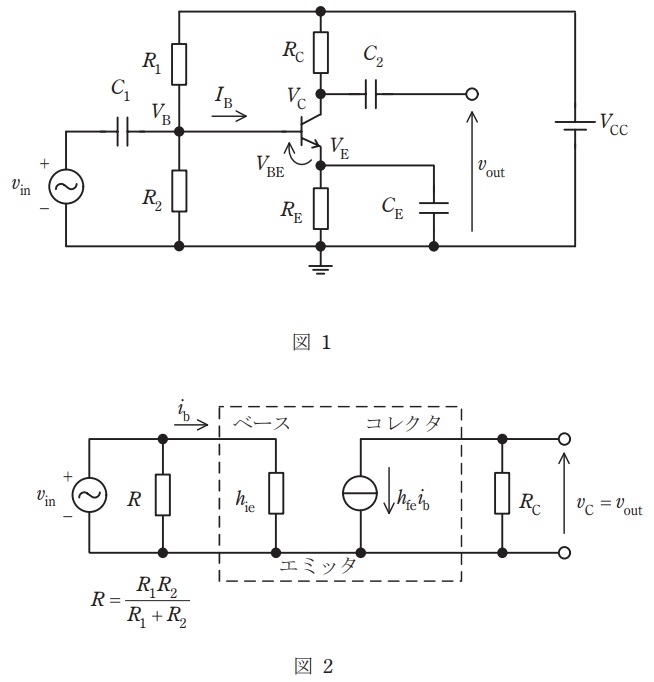
図1に示す回路において,まず\( \ v_{\mathrm {in}}=0 \ \)として各節点のバイアス電位を求める。バイポーラトランジスタのベース電流\( \ I_{\mathrm {B}} \ \)が十分に小さく零とみなせるとき,ベース電位\( \ V_{\mathrm {B}} \ \)は\( \ \fbox { (1) } \ \)となる。バイポーラトランジスタのベース・エミッタ間電圧を\( \ V_{\mathrm {BE}} \ \)とすると,エミッタ電位\( \ V_{\mathrm {E}} \ \)は\( \ \fbox { (1) } \ -V_{\mathrm {BE}} \ \)となり,コレクタ電位\( \ V_{\mathrm {C}} \ \)は,\( \ V_{\mathrm {E}} \ \)を用いて\( \ \fbox { (2) } \ \)となる。
次に,図1に微小な交流電圧\( \ v_{\mathrm {in}} \ \)を入力した際のコレクタ電位の変化量\( \ v_{\mathrm {C}} \ \)を求める。図2は図1の交流等価回路である。図2の破線部はバイポーラトランジスタの交流等価回路であり,\( \ h_{\mathrm {ie}} \ \)と\( \ h_{\mathrm {fe}} \ \)はそれぞれバイポーラトランジスタの出力短絡入力インピーダンスとエミッタ接地電流増幅率である。また,各容量は,信号の周波数においてインピーダンスが十分に小さいため短絡とみなせるとする。\( \ v_{\mathrm {in}} \ \)を加えた際のコレクタ電位の変化量\( \ v_{\mathrm {C}} \ \)は,図2の\( \ v_{\mathrm {C}} \ \)を求めることで\( \ \fbox { (3) } \ \times v_{\mathrm {in}} \ \)と求まる。増幅回路の出力電圧\( \ v_{\mathrm {out}} \ \)は\( \ v_{\mathrm {C}} \ \)と等しいため増幅回路の電圧増幅率\( \ \displaystyle \frac {v_{\mathrm {out}}}{v_{\mathrm {in}}} \ \)は\( \ \fbox { (3) } \ \)となる。
\( \ v_{\mathrm {in}} \ \)として正弦波電圧を加える場合を考える。ここで,図1の回路はコレクタ電位が\( \ V_{\mathrm {E}} \ \)から\( \ V_{\mathrm {CC}} \ \)の間にあるとき,ひずみなく動作するとする。図1の回路に\( \ v_{\mathrm {in}} \ \)を加えた際のコレクタ電位は\( \ V_{\mathrm {C}}+v_{\mathrm {C}} \ \)であるから,\( \ v_{\mathrm {out}} \ \)として振幅\( \ V_{\mathrm {1}} \ \)の正弦波電圧をひずみなく出力するためには,\( \ V_{\mathrm {C}} \ \)は\( \ \fbox { (4) } \ \)を満たさなければならない。次に,一定の振幅の正弦波電圧\( \ v_{\mathrm {in}} \ \)を加えた状態で,出力電圧波形を観察しながら,\( \ R_{\mathrm {C}} \ \)を\( \ \displaystyle V_{\mathrm {C}}=\frac {V_{\mathrm {CC}}+V_{\mathrm {E}}}{2} \ \)となる値から徐々に増加させた。\( \ R_{\mathrm {C}} \ \)の増加に伴い出力電圧の振幅は増加するが,\( \ V_{\mathrm {C}} \ \)は\( \ \fbox { (2) } \ \)であるため,\( \ R_{\mathrm {C}} \ \)を更に増加させると,やがて正弦波状の出力電圧波形は\( \ \fbox { (5) } \ \)ひずむ。
〔問7の解答群〕
\[
\begin{eqnarray}
&(イ)& V_{\mathrm {BE}} &(ロ)& \frac {R_{2}}{R_{1}+R_{2}}V_{\mathrm {CC}} &(ハ)& 上側から \\[ 5pt ]
&(ニ)& -h_{\mathrm {ie}}h_{\mathrm {fe}}R_{\mathrm {C}} &(ホ)& 下側から &(ヘ)& V_{\mathrm {E}}-V_{\mathrm {1}}≦V_{\mathrm {C}}≦V_{\mathrm {CC}}-V_{\mathrm {1}} \\[ 5pt ]
&(ト)& V_{\mathrm {CC}}-\frac {R_{\mathrm {C}}}{R_{\mathrm {E}}}V_{\mathrm {E}} &(チ)& -\frac {h_{\mathrm {fe}}R_{\mathrm {C}}}{h_{\mathrm {ie}}} &(リ)& V_{\mathrm {E}}+V_{\mathrm {1}}≦V_{\mathrm {C}}≦V_{\mathrm {CC}}-V_{\mathrm {1}} \\[ 5pt ]
&(ヌ)& \frac {R_{\mathrm {C}}}{R_{\mathrm {E}}}V_{\mathrm {E}} &(ル)& \frac {R_{1}}{R_{1}+R_{2}}V_{\mathrm {CC}} &(ヲ)& V_{\mathrm {E}}≦V_{\mathrm {C}}≦V_{\mathrm {CC}} \\[ 5pt ]
&(ワ)& -\frac {h_{\mathrm {ie}}R_{\mathrm {C}}}{h_{\mathrm {fe}}} &(カ)& V_{\mathrm {CC}}-R_{\mathrm {C}}V_{\mathrm {E}} &(ヨ)& 上側と下側が同時に \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
エミッタ接地増幅回路と小信号等価回路に関する問題です。
基本的には選択問題で出題される内容ですが,慣れてしまうと計算パターンや解法も決まっているため点取り問題となります。
平成29年問7に類題が出題されていますので,合わせて学習しておくようにして下さい。
【解答】
(1)解答:ロ
図1-1に示す閉回路に分圧の法則を適用すると,
\[
\begin{eqnarray}
V_{\mathrm {B}} &=&\frac {R_{2}}{R_{1}+R_{2}}V_{\mathrm {CC}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
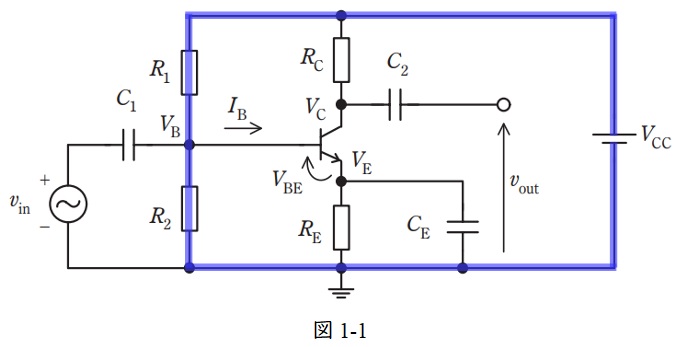
(2)解答:ト
エミッタ電流\( \ I_{\mathrm {E}} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {E}} &=&\frac {V_{\mathrm {E}}}{R_{\mathrm {E}}} \\[ 5pt ]
\end{eqnarray}
\]
であり,ベース電流\( \ I_{\mathrm {B}} \ \)は十分に小さく零とみなせるので,
\[
\begin{eqnarray}
I_{\mathrm {C}} &≒&I_{\mathrm {E}} \\[ 5pt ]
&=&\frac {V_{\mathrm {E}}}{R_{\mathrm {E}}} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,コレクタ電圧\( \ V_{\mathrm {C}} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {C}} &=&V_{\mathrm {CC}}-R_{\mathrm {C}}I_{\mathrm {C}} \\[ 5pt ]
&=&V_{\mathrm {CC}}-\frac {R_{\mathrm {C}}}{R_{\mathrm {E}}}V_{\mathrm {E}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:チ
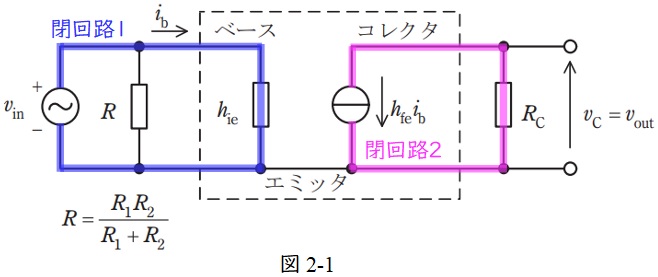
図2-1に示す閉回路1について,
\[
\begin{eqnarray}
v_{\mathrm {in}} &=&h_{\mathrm {ie}}i_{\mathrm {b}} \\[ 5pt ]
\end{eqnarray}
\]
であり,閉回路2について,
\[
\begin{eqnarray}
v_{\mathrm {out}} &=&-R_{\mathrm {C}}h_{\mathrm {fe}}i_{\mathrm {b}} \\[ 5pt ]
\end{eqnarray}
\]
であるから,
\[
\begin{eqnarray}
\frac {v_{\mathrm {out}}}{v_{\mathrm {in}}} &=&\frac {-R_{\mathrm {C}}h_{\mathrm {fe}}i_{\mathrm {b}}}{h_{\mathrm {ie}}i_{\mathrm {b}}} \\[ 5pt ]
&=&-\frac {h_{\mathrm {fe}}R_{\mathrm {C}}}{h_{\mathrm {ie}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:リ
コレクタ電位は\( \ V_{\mathrm {C}}+v_{\mathrm {C}}=V_{\mathrm {C}}+v_{\mathrm {out}} \ \)であり,\( \ v_{\mathrm {out}} \ \)として振幅\( \ V_{\mathrm {1}} \ \)の正弦波電圧\( \ V_{\mathrm {1}}\sin \omega t \ \)を加えたときのコレクタ電位は,
\[
\begin{eqnarray}
V_{\mathrm {C}}+v_{\mathrm {C}} &=&V_{\mathrm {C}}+V_{\mathrm {1}}\sin \omega t \\[ 5pt ]
\end{eqnarray}
\]
となる。このコレクタ電位\( \ V_{\mathrm {C}}+V_{\mathrm {1}}\sin \omega t \ \)が常に\( \ V_{\mathrm {E}}≦V_{\mathrm {C}}+V_{\mathrm {1}}\sin \omega t≦V_{\mathrm {CC}} \ \)を満たせばひずみなく出力するので,
\[
\begin{eqnarray}
V_{\mathrm {C}}+V_{\mathrm {1}} &≦&V_{\mathrm {CC}} \\[ 5pt ]
V_{\mathrm {C}} &≦&V_{\mathrm {CC}}-V_{\mathrm {1}} \\[ 5pt ]
V_{\mathrm {C}}-V_{\mathrm {1}} &≧&V_{\mathrm {E}} \\[ 5pt ]
V_{\mathrm {C}} &≧&V_{\mathrm {E}}+V_{\mathrm {1}} \\[ 5pt ]
\end{eqnarray}
\]
すなわち,\( \ V_{\mathrm {E}}+V_{\mathrm {1}}≦V_{\mathrm {C}}≦V_{\mathrm {CC}}-V_{\mathrm {1}} \ \)を満たさなければならないことがわかる。
(5)解答:ホ
(2)解答式より,\( \ R_{\mathrm {C}} \ \)を増加すると\( \ V_{\mathrm {C}} \ \)が低下するため,出力\( \ v_{\mathrm {out}} \ \)の振動の中心の電位が低下することになる。
そのため,正弦波状の出力電圧波形は下側からひずむことになる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん