《機械・制御》〈同期機〉[R06:問1]同期機の無負荷飽和曲線と三相短絡特性曲線に関する計算・論説問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

同期機の特性に関して，次の問に答えよ。

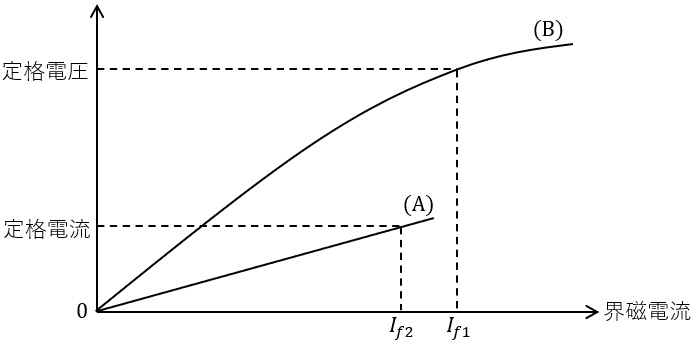
(1)　図に同期機の無負荷飽和曲線と三相短絡特性曲線を示している。

　(a)　図中の\( \ \left( \mathrm {A} \right) \ \)はどちらの特性曲線か示せ。また，この特性曲線を得る試験方法を\( \ 100 \ \)字程度以内で述べよ。

　(b)　図中の\( \ \left( \mathrm {B} \right) \ \)はどちらの特性曲線か示せ。また，この特性曲線を得る試験方法を\( \ 100 \ \)字程度以内で述べよ。

(2)　定格電圧\( \ 200 \ \mathrm {V} \ \)，定格電流\( \ 144.3 \ \mathrm {A} \ \)，\( \ 50 \ \mathrm {Hz} \ \)の三相同期発電機を試験した結果，図中の\( \ I_{f1} \ \)，\( \ I_{f2} \ \)はそれぞれ\( \ I_{f1}=2.8 \ \mathrm {A} \ \)，\( \ I_{f2}=2.5 \ \mathrm {A} \ \)として得られた。

　(a)　この同期発電機の定格容量\( \ \mathrm {[kV\cdot A]} \ \)を求めよ。

　(b)　この同期発電機の単位法で表した同期インピーダンス\( \ \mathrm {[p.u.]} \ \)を求めよ。

【ワンポイント解説】

同期機の無負荷飽和曲線と三相短絡特性曲線に関する問題です。
\( \ 3 \ \)種でも学習する範囲ですが，うろ覚えですと解けない問題です。\( \ 2 \ \)種保持者は十分に指導者レベルと言えるので，特性曲線については何も見ずに説明できるぐらいを目指すようにしましょう。

1.同期発電機の無負荷飽和曲線と三相短絡曲線
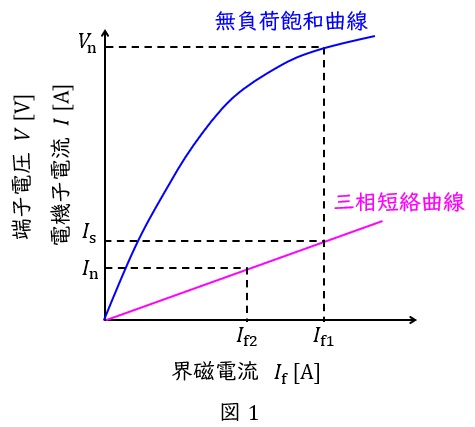
同期発電機は図1のような無負荷飽和曲線と三相短絡曲線の特性があります。
無負荷飽和曲線は定格速度で無負荷で運転したときの界磁電流と端子電圧の関係，三相短絡曲線は電機子巻線の三相の出力端子を短絡し定格速度で運転したときの界磁電流と三相短絡電流の関係，を表したものです。
図中の\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \)は定格電圧，\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)は定格電流，無負荷飽和曲線は磁気飽和により曲線となり，三相短絡曲線は曲線ですが，ほぼ比例の直線と近似できます。
この時，\( \ I_{\mathrm {s}} \ \mathrm {[A]} \ \)は定格電圧時の三相短絡電流であり，短絡比\( \ K \ \)は，
\[
\begin{eqnarray}
K &=& \frac {I_{\mathrm {s}}}{I_{\mathrm {n}}}=\frac {I_{\mathrm {f1}}}{I_{\mathrm {f2}}} \\[ 5pt ] \end{eqnarray}
\] となります。

2.オーム法から単位法への変換
基準容量を\( \ P_{\mathrm {n}} \ \mathrm {[V\cdot A]} \ \)，基準電圧を\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \)，基準電流を\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)とすると，\( \ Z \ \mathrm {[\Omega ]} \ \)の単位法で表したインピーダンス\( \ Z \ \mathrm {[p.u.]} \ \)は，
\[
\begin{eqnarray}
Z \ \mathrm {[p.u.]} \ &=&\frac {Z \ \mathrm {[\Omega ]} \ I_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}　　 (定義) \\[ 5pt ] &=&\frac {\sqrt {3}Z \ \mathrm {[\Omega ]} \ I_{\mathrm {n}}}{V_{\mathrm {n}}} \\[ 5pt ] &=&\frac {\sqrt {3}Z \ \mathrm {[\Omega ]} \ V_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}} \\[ 5pt ] &=&\frac {P_{\mathrm {n}}Z \ \mathrm {[\Omega ]} \ }{V_{\mathrm {n}}^{2}}　　 (∵P_{\mathrm {n}}=\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} ) \\[ 5pt ] \end{eqnarray}
\] となります。

3.単位法で表した同期インピーダンスと短絡比の関係
同期発電機の単位法で表した同期インピーダンスが\( \ Z \ \mathrm {[p.u.]} \ \)，短絡比が\( \ K \ \)であるとき，
\[
\begin{eqnarray}
K&=&\frac {1}{Z \ \mathrm {[p.u.]}} \\[ 5pt ] \end{eqnarray}
\] の関係があります。

※単位法の定義式等を用いて\( \ \displaystyle I_{\mathrm {s}}=\frac {V_{\mathrm {n}}}{\sqrt {3}Z \ \mathrm {[\Omega ]}} \ \)から上式を求めることはできますが，試験時には暗記しておいた方が良いと思います。
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}{Z \ \mathrm {[\Omega ]}} \\[ 5pt ] &=&\frac {V_{\mathrm {n}}}{\sqrt {3}Z \ \mathrm {[\Omega ]}} \\[ 5pt ] \frac {I_{\mathrm {s}}}{I_{\mathrm {n}}}&=&\frac {V_{\mathrm {n}}}{\sqrt {3}Z \ \mathrm {[\Omega ]}I_{\mathrm {n}}} \\[ 5pt ] K&=&\frac {1}{Z} \\[ 5pt ] \end{eqnarray}
\]

【解答】

(1)(a)\( \ \left( \mathrm {A} \right) \ \)の特性曲線と特性曲線を得る試験方法
(ポイント)
・ワンポイント解説「1.同期発電機の無負荷飽和曲線と三相短絡曲線」の通りです。
・「三相短絡」していることと「定格速度で回転」させていることを記載すれば高得点が得られるかと思います。

(試験センター解答例)
\( \ \left( \mathrm {A} \right) \ \)の特性曲線は三相短絡特性曲線である。
この特性曲線は，同期機の電機子端子を三相全て短絡し，定格速度で回転させたとき，界磁電流を変化させて電機子短絡電流を測定する試験により得られる。

(1)(b)\( \ \left( \mathrm {B} \right) \ \)の特性曲線と特性曲線を得る試験方法
(ポイント)
・ワンポイント解説「1.同期発電機の無負荷飽和曲線と三相短絡曲線」の通りです。
・「三相開放（無負荷）」していることと「定格速度で回転」させていることを記載すれば高得点が得られるかと思います。

(試験センター解答例)
\( \ \left( \mathrm {B} \right) \ \)の特性曲線は無負荷飽和曲線である。
この特性曲線は，同期機の電機子端子を三相全て開放し，定格速度で回転させたとき，界磁電流を変化させて電機子端子電圧を測定する試験により得られる。

(1)(c)短絡比の定義
(ポイント)
・ワンポイント解説「1.同期発電機の無負荷飽和曲線と三相短絡曲線」の通りです。
・図1の\( \ \displaystyle \frac {I_{\mathrm {s}}}{I_{\mathrm {n}}} \ \)を言葉で説明すれば十分に高得点を得られるでしょう。

(試験センター解答例)
短絡比とは，定格速度で回転させ，端子開放時に定格電圧を発生させる界磁電流において，電機子端子を三相短絡したと仮定したときの持続短絡電流の定格電流に対する比である。

(2)(a)同期発電機の定格容量\( \ \mathrm {[kV\cdot A]} \ \)
定格電圧\( \ V_{\mathrm {n}}=200 \ \mathrm {[V]} \ \)，定格電流\( \ I_{\mathrm {n}}=144.3 \ \mathrm {[A]} \ \)なので，定格容量\( \ P_{\mathrm {n}} \ \mathrm {[kV\cdot A]} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {n}}&=&\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} \\[ 5pt ] &=&\sqrt {3}\times 200 \times 144.3 \\[ 5pt ] &≒&49 \ 987 \ \mathrm {[V\cdot A]}　→　50.0 \ \mathrm {[kV\cdot A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)(b)同期発電機の単位法で表した同期インピーダンス\( \ \mathrm {[p.u.]} \ \)
短絡比の定義より短絡比\( \ K \ \)は，ワンポイント解説「1.同期発電機の無負荷飽和曲線と三相短絡曲線」の通り，
\[
\begin{eqnarray}
K&=&\frac {I_{f1}}{I_{f2}} \\[ 5pt ] &=&\frac {2.8}{2.5} \\[ 5pt ] &=&1.12 \\[ 5pt ] \end{eqnarray}
\] なので，単位法で表した同期インピーダンス\( \ Z \ \mathrm {[p.u.]} \ \)は，ワンポイント解説「3.単位法で表した同期インピーダンスと短絡比の関係」の通り，
\[
\begin{eqnarray}
Z&=&\frac {1}{K} \\[ 5pt ] &=&\frac {1}{1.12} \\[ 5pt ] &≒&0.892 \ 86　→　0.893 \ \mathrm {[p.u.]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)(c)同期発電機の同期インピーダンス\( \ \mathrm {[\Omega ]} \ \)
(2)(b)解答及び単位法の定義より，同期インピーダンス\( \ Z \ \mathrm {[\Omega ]} \ \)は，ワンポイント解説「2.オーム法から単位法への変換」の通り，
\[
\begin{eqnarray}
Z \ \mathrm {[p.u.]} &=&\frac {\sqrt {3}Z \ \mathrm {[\Omega ]} \ I_{\mathrm {n}}}{V_{\mathrm {n}}} \\[ 5pt ] Z \ \mathrm {[\Omega ]}&=&\frac {Z \ \mathrm {[p.u.]} \ V_{\mathrm {n}}}{\sqrt {3}I_{\mathrm {n}}} \\[ 5pt ] &=&\frac {0.892 \ 86\times 200}{\sqrt {3}\times 144.3} \\[ 5pt ] &≒&0.714 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。