《機械・制御》〈回転機〉[H27:問1]同期発電機の送電電力に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★☆☆☆☆（易しい）

同期リアクタンス\(X_{\mathrm {s}} \ [\Omega ]\)の同期発電機をインピーダンスが十分に小さい相電圧\(V_{0} \ \mathrm {[V ]}\)の三相交流系統に接続し，発電機に\(P_{0} \ \mathrm {[W]}\)の機械的入力を加えたとき，内部相差角は\(\delta _{0}=45°\)で動作した。界磁電流及び回転速度は一定で，発電機の突極性及び損失は無視できるものとする。

(1)　同期発電機を相電圧\(V_{0}\)の三相交流系統に接続した場合について，以下のa.及びb.に答えよ。

a.発電機に加える機械的入力を\(P_{1} \ \mathrm {[W]}\)にすると，内部相差角は\(\delta _{1}=30°\)となった。機械的入力の比\(\displaystyle \frac {P_{1}}{P_{0}}\)を求めよ。

b.発電機と交流系統の間に\(X_{2}=X_{\mathrm{s}}\)のリアクトルを挿入した。\(P_{2} \ \mathrm {[W]}\)の機械的入力を加えると，交流系統電圧と無負荷誘導起電力の間の位相角が\(\delta _{2}=45°\)に増加した。このときの機械的入力の比\(\displaystyle \frac {P_{2}}{P_{0}}\)を求めよ。

(2)　同期発電機を三相交流系統から切り離して\(R \ [\Omega ]\)の抵抗器を\(\mathrm {Y}\)結線して接続し，抵抗器だけに電力を供給する。ここで，\(P_{3}=P_{0} \ \mathrm {[W]}\)の機械的入力を加えたところ，発電機端子の相電圧は\(V_{3} \ \mathrm {[V ]}\)，内部相差角は\(\delta _{3}=60°\)となった。抵抗器だけを接続した場合について，以下のa.及びb.に答えよ。

a.発電機端子の相電圧の比\(\displaystyle \frac {V_{3}}{V_{0}}\)を求めよ。

b.同期リアクタンス\(X_{\mathrm {s}}\)に対する抵抗\(R\)の比\(\displaystyle \frac {R}{X_{\mathrm {s}}}\)を求めよ。

【ワンポイント解説】

電験二種の二次試験としてはかなり易しい部類の問題となります。計算間違いもしにくい問題なので，丁寧に解いて確実に完答できるようにしたいところです。

1.同期機の1相分の出力\(P\)
誘導起電力を\(E \ \mathrm {[V ]}\)，端子電圧を\(V \ \mathrm {[V ]}\)，同期リアクタンスを\(X_{\mathrm {s}} \ [\Omega ]\)，内部相差角を\(\delta \)とすると，1相分の出力\(P \ \mathrm {[W ]}\)は，
\[
P=\frac {VE}{X_{\mathrm {s}}}\sin \delta
\] となります。

【解答】

(1)a.機械的入力の比\(\displaystyle \frac {P_{1}}{P_{0}}\)
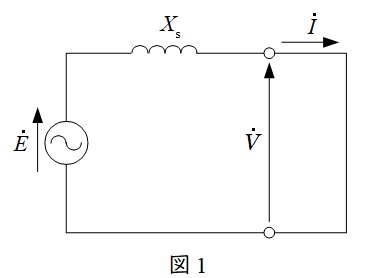
題意に沿って1相分の回路図を描くと図1の通りとなる。誘導起電力の大きさを\(E\)とすると，ワンポイント解説「1.同期機の1相分の出力\(P\)」より，発電機出力\(P_{0}\)は，
\[
P_{0}=\frac {3V_{0}E}{X_{\mathrm {s}}}\sin \delta _{0}
\] 発電機出力\(P_{1}\)は，
\[
P_{1}=\frac {3V_{0}E}{X_{\mathrm {s}}}\sin \delta _{1}
\] となるので，機械的入力の比\(\displaystyle \frac {P_{1}}{P_{0}}\)は，
\[
\begin{eqnarray}
\frac {P_{1}}{P_{0}}&=& \frac {\frac {3V_{0}E}{X_{\mathrm {s}}}\sin \delta _{1}}{\frac {3V_{0}E}{X_{\mathrm {s}}}\sin \delta _{0}} \\[ 5pt ] &=& \frac {\sin \delta _{1}}{\sin \delta _{0}} \\[ 5pt ] &=& \frac {\sin 30°}{\sin 45°} \\[ 5pt ] &=& \frac {\frac {1}{2}}{\frac {\sqrt {2}}{2}} \\[ 5pt ] &≒&0.707 \\[ 5pt ] \end{eqnarray}
\] と求められる。

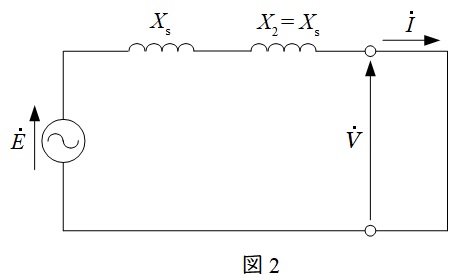
(1)b.機械的入力の比\(\displaystyle \frac {P_{2}}{P_{0}}\)
題意に沿って1相分の回路図を描くと図2の通りとなる。発電機出力\(P_{2}\)は，
\[
\begin{eqnarray}
P_{2}&=& \frac {3V_{0}E}{X_{\mathrm {s}}+X_{2}}\sin \delta _{2} \\[ 5pt ] &=& \frac {3V_{0}E}{2X_{\mathrm {s}}}\sin \delta _{0}\\[ 5pt ] \end{eqnarray}
\] となるので，機械的入力の比\(\displaystyle \frac {P_{2}}{P_{0}}\)は，
\[
\begin{eqnarray}
\frac {P_{2}}{P_{0}}&=& \frac {\frac {3V_{0}E}{2X_{\mathrm {s}}}\sin \delta _{0}}{\frac {3V_{0}E}{X_{\mathrm {s}}}\sin \delta _{0}} \\[ 5pt ] &=& \frac {1}{2} \\[ 5pt ] &=& 0.5 \\[ 5pt ] \end{eqnarray}
\] と求められる。

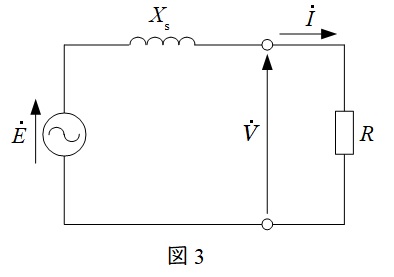
(2)a.発電機端子の相電圧の比\(\displaystyle \frac {V_{3}}{V_{0}}\)
題意に沿って1相分の回路図を描くと図3の通りとなる。発電機出力\(P_{3}\)は，
\[
P_{3}= \frac {3V_{3}E}{X_{\mathrm {s}}}\sin \delta _{3}
\] となり，題意より\(P_{0}=P_{3}\)なので，
\[
\begin{eqnarray}
P_{0}&=& P_{3} \\[ 5pt ] \frac {3V_{0}E}{X_{\mathrm {s}}}\sin \delta _{0}&=& \frac {3V_{3}E}{X_{\mathrm {s}}}\sin \delta _{3}\\[ 5pt ] V_{0}\sin \delta _{0}&=& V_{3}\sin \delta _{3}\\[ 5pt ] \frac {V_{3}}{V_{0}}&=& \frac {\sin \delta _{0}}{\sin \delta _{3}}\\[ 5pt ] &=& \frac {\sin 45°}{\sin 60°}\\[ 5pt ] &=& \frac {\frac {\sqrt {2}}{2}}{\frac {\sqrt {3}}{2}}\\[ 5pt ] &≒&0.816 \\[ 5pt ] \end{eqnarray}
\] と求められる。

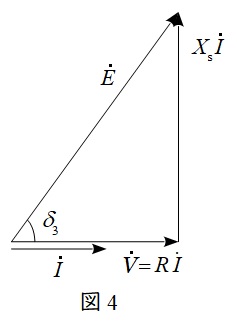
(2)b.同期リアクタンス\(X_{\mathrm {s}}\)に対する抵抗\(R\)の比\(\displaystyle \frac {R}{X_{\mathrm {s}}}\)
題意に沿ってベクトル図を描くと図4の通りとなる。図4より，\(\delta _{3}=60°\)であるから，同期リアクタンス\(X_{\mathrm {s}}\)と抵抗\(R\)の関係は，
\[
\begin{eqnarray}
X_{\mathrm {s}}I&=& \sqrt {3}RI \\[ 5pt ] \frac {R}{X_{\mathrm {s}}}&=& \frac {1}{\sqrt {3}}\\[ 5pt ] &≒&0.577 \\[ 5pt ] \end{eqnarray}
\] と求められる。