《理論》〈半導体〉[H30:問4]半導体のキャリア濃度に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，半導体のキャリア濃度に関する記述である。文中の$\fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$}$に当てはまる最も適切なものを解答群の中から選べ。

熱平衡状態にある半導体では，正孔濃度$ \ p \ $と電子濃度$ \ n \ $の積，すなわち$ \ \mathrm {pn} \ $積は一定となる性質がある。不純物ドーピングを行っていない真性半導体では，$ \ p \ $と$ \ n \ $は常に等しい。このとき，$ \ p=n \ $を真性キャリア濃度$ \ n_{\mathrm {i}} \ $と定義すると，$ \ \mathrm {pn} \ $積は$ \ n_{\mathrm {i}} \ $を用いて$\fbox {　（１）　}$と表される。不純物ドーピングを行うと，不純物イオンから供給される正孔又は電子によって，$ \ p≠n \ $となるが，$ \ \mathrm {pn} \ $積一定の関係から，多数キャリア濃度が決まると少数キャリア濃度も決まる。ただし，$ \ n_{\mathrm {i}} \ $は温度上昇に伴い顕著に増加する。本問では，室温における$ \ n_{\mathrm {i}} \ $が$ \ 1.0 \times 10^{10} \ \mathrm {cm}^{-3}$であり，また，温度が室温から$40$℃上昇すると$ \ n_{\mathrm {i}} \ $が$10$倍に増加する半導体を考える。半導体の導電率は，電子及び正孔による導電率の和で表され，それぞれの導電率はそれぞれの濃度及び移動度に比例すると仮定すると，真性半導体の導電率は室温から$40$℃の温度上昇により$\fbox {　（２）　}$倍となる。ただし，移動度の温度変化は無視する。

この半導体にドナー不純物を$ \ 1.0\times 10^{18} \ \mathrm {cm}^{-3} \ $ドーピングしたところ，不純物濃度と等しい電子濃度を有する$ \ \mathrm {n} \ $形半導体となった。この半導体の室温における正孔濃度は$\fbox {　（３）　} \ \mathrm {cm}^{-3} \ $である。また，室温から温度が$40$℃上昇した場合の正孔濃度は$\fbox {　（４）　} \ \mathrm {cm}^{-3} \ $となる。ただし，多数キャリアである電子濃度は$40$℃の温度上昇では変化せず，不純物濃度は等しいものとしてよい。この場合，導電率は室温から$40$℃の温度上昇により約$\fbox {　（５）　}$倍となる。ただし，電子移動度と正孔移動度は等しいと仮定し，温度依存性はないものとする。

〔問4の解答群〕
\[
\begin{eqnarray}
&（イ）&　1.0\times 10^{-7}　　　&（ロ）&　1.0\times 10^{2}　　　&（ハ）&　5.0\times 10^{3} \\[ 5pt ] &（ニ）&　\frac {n_{\mathrm {i}}^{2}}{2}　　　&（ホ）&　0.1　　　&（ヘ）&　n_{\mathrm {i}}^{2} \\[ 5pt ] &（ト）&　20　　　&（チ）&　1.0\times 10^{-2}　　　　&（リ）&　50 \\[ 5pt ] &（ヌ）&　1.0\times 10^{-8}　　　&（ル）&　1.0\times 10^{4}　　　&（ヲ）&　1.0 \\[ 5pt ] &（ワ）&　n_{\mathrm {i}}　　　&（カ）&　1.0\times 10^{-4}　　　&（ヨ）&　10 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

半導体の導電率に関する問題です。半導体では電子及び正孔が移動することで電気を流すことになります。なかなか出題されにくい傾向の問題なので，三種の時には勉強されていない方もいらっしゃるかもしれません。
三種の場合わからなくても100点中5点を失うだけですが，二種の場合本問を取り逃すと90点中15点を失うことになりますので，かなり大きなダメージを追います。したがって，こういう分野も少しずつ勉強するようにしましょう。

1.真性半導体
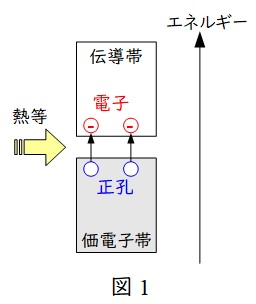
正孔濃度と電子濃度が同じである半導体で，基本的には周期表で4価の原子であるケイ素$\mathrm {Si}$の事を指します。常温ではキャリア濃度があまり高くなく，抵抗率も高いため絶縁体に近い特性がありますが，熱等のエネルギーを加えると，誘起される電子の数が増え，導電性が上がる性質があります。
イメージとしては図1に示すようなエネルギーバンド構造が理解しやすいと思いますが，熱等を加えることにより，価電子帯（低エネルギー帯）にいる電子が励起され伝導体に移動することで，電子と正孔対ができ，電気を流しやすくなる性質を持ちます。

2.不純物半導体
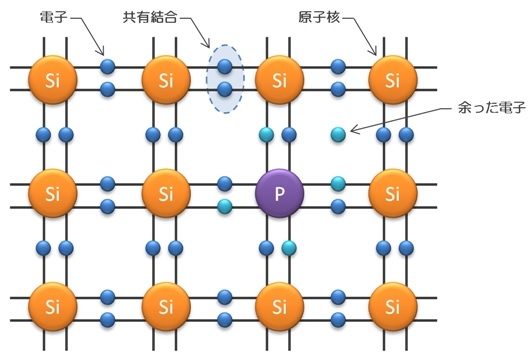
真性半導体に5価のリン$\mathrm {P}$やヒ素$\mathrm {As}$を混ぜる(ドープする)ことで，電子が余る状態を作り，余った電子が導通することで，真性半導体よりも電気が流れやすくなったもの，もしくは，真性半導体に3価のホウ素$\mathrm {B}$を混ぜる(ドープする)ことで，正孔ができる状態を作り，正孔が導通することで，真性半導体よりも電気が流れやすくなったものを言います。電子や正孔をキャリアと言い，多くあるキャリアを多数キャリアと言います。
一般に電子を多数キャリアとする半導体を$ \ \mathrm {n} \ $形半導体，正孔を多数キャリアとする半導体を$ \ \mathrm {p} \ $形半導体と言います。

出典：LED発光ダイオードの基礎知識　ＨＰ
http://www.optdevice.jp/semiconductor/intrinsic.html

【解答】

(1)解答：ヘ
題意より，真性キャリア濃度が$ \ n_{\mathrm {i}} \ $であるから，$ \ \mathrm {pn} \ $積は，
\[
\begin{eqnarray}
pn &=& n_{\mathrm {i}}\times n_{\mathrm {i}} \\[ 5pt ] &=& n_{\mathrm {i}}^{2} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ヨ
半導体の導電率は電子及び正孔の導電率の和で表され，導電率はキャリア濃度に比例するので，室温の時の導電率を$\sigma _{1}$，$40$℃上昇した時の導電率を$\sigma _{2}$とすると，
\[
\begin{eqnarray}
\frac {\sigma _{2}}{\sigma _{1}} &=& \frac {10\mathrm {n}+10\mathrm {p}}{\mathrm {n}+\mathrm {p}} \\[ 5pt ] &=& \frac {10n_{\mathrm {i}}+10n_{\mathrm {i}}}{n_{\mathrm {i}}+n_{\mathrm {i}}} \\[ 5pt ] &=& 10 \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ロ
題意より，$ \ \mathrm {pn} \ $積は一定であり，電子濃度$ \ n=1.0\times 10^{18} \ \mathrm {cm}^{-3} \ $であるから，
\[
\begin{eqnarray}
pn &=& n_{\mathrm {i}}^{2} \\[ 5pt ] p\times 1.0\times 10^{18} &=& \left( 1.0 \times 10^{10}\right) ^{2} \\[ 5pt ] p&=& 1.0 \times 10^{2} \ \mathrm {cm}^{-3} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ル
温度が$40$℃上昇すると，$ \ \mathrm {pn} \ $積は，
\[
\begin{eqnarray}
pn &=& 10 n_{\mathrm {i}}\times 10 n_{\mathrm {i}} \\[ 5pt ] &=& 100 n_{\mathrm {i}}^{2} \\[ 5pt ] \end{eqnarray}
\] となる。多数キャリア濃度は変化しないので，$40$℃上昇後の正孔濃度を$ \ p^{\prime } \ $とすると，
\[
\begin{eqnarray}
p^{\prime }n &=& 100 n_{\mathrm {i}}^{2}\\[ 5pt ] p^{\prime }\times 1.0\times 10^{18} &=& 100 \times \left( 1.0 \times 10^{10}\right) ^{2} \\[ 5pt ] p^{\prime }&=& 1.0 \times 10^{4} \ \mathrm {cm}^{-3} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ヲ
室温の時の導電率を$\sigma _{1}^{\prime }$，$40$℃上昇した時の導電率を$\sigma _{2}^{\prime }$とすると，
\[
\begin{eqnarray}
\frac {\sigma _{2}^{\prime }}{\sigma _{1}^{\prime }} &=& \frac {n+p^{\prime }}{n+p} \\[ 5pt ] &=& \frac {1.0\times 10^{18}+1.0\times 10^{4}}{1.0\times 10^{18}+1.0\times 10^{2}} \\[ 5pt ] &≒& 1 \\[ 5pt ] \end{eqnarray}
\] と求められる。