Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
図1は,受変電設備の一部を表した単線結線図である。容量\( \ P_{\mathrm {T}}=12 \ 000 \ \mathrm {kV\cdot A} \ \)の変圧器から,容量\( \ P_{\mathrm {1}}=6 \ 000 \ \mathrm {kW} \ \)で,力率\( \ \cos \theta _{\mathrm {1}}=0.8 \ \)(遅れ)の負荷に電力を供給しており,変圧器の\( \ 2 \ \)次側には,力率改善用コンデンサ\( \ Q_{\mathrm {1}}=2 \ 000 \ \mathrm {kvar} \ \)が投入されている。この設備において,次の問に答えよ。なお,力率改善用コンデンサの直列リアクトルは考慮しなくてよい。
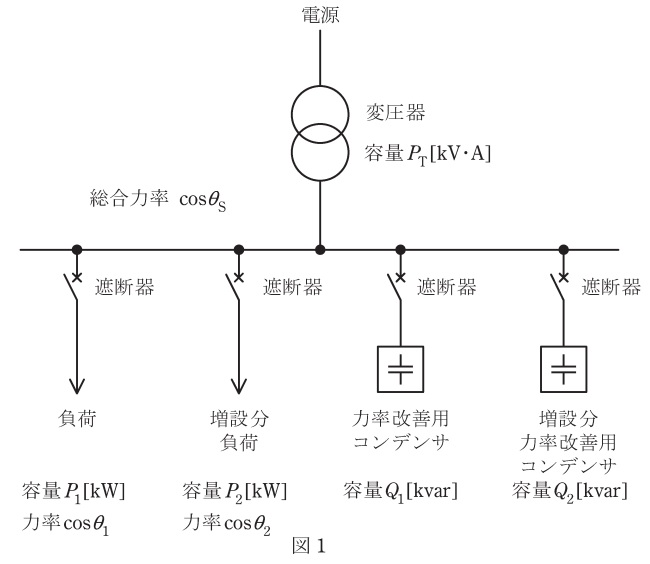
(1) 上記の運用状況をベクトル図に表すと,図2のようになる。この運用に,さらに容量\( \ P_{\mathrm {2}}=4 \ 500 \ \mathrm {kW} \ \)で,力率\( \ \cos \theta _{\mathrm {2}}=0.6 \ \)(遅れ)の負荷を増設すると,変圧器は過負荷になるおそれがある。そこで,変圧器を過負荷にしないためには,増設分の力率改善用コンデンサの容量\( \ Q_{\mathrm {2}} \ \mathrm {[kvar]} \ \)は,少なくともいくら必要か。また,このときの総合力率\( \ \cos \theta _{\mathrm {S}} \ \)はいくらになるか。
(2) 答案用紙に印刷されている図2に,\( \ P_{\mathrm {2}} \ \mathrm {[kW]} \ \),\( \ Q_{\mathrm {2}} \ \mathrm {[kvar]} \ \)のベクトル図と,力率角\( \ \cos \theta _{\mathrm {2}} \ \)を追記せよ。
(3) 総合力率を\( \ \cos \theta _{\mathrm {S}}=0.95 \ \)(遅れ)にするためには,増設する力率改善用コンデンサの容量\( \ Q_{\mathrm {2}} \ \mathrm {[kvar]} \ \)はいくら必要か。
【ワンポイント解説】
\( \ 3 \ \)種の法規科目の電気施設管理でも定番となっている力率改善に関する問題です。
難解な公式を使用しませんが,計算量が若干多いため,計算間違いに注意して解くようにしましょう。
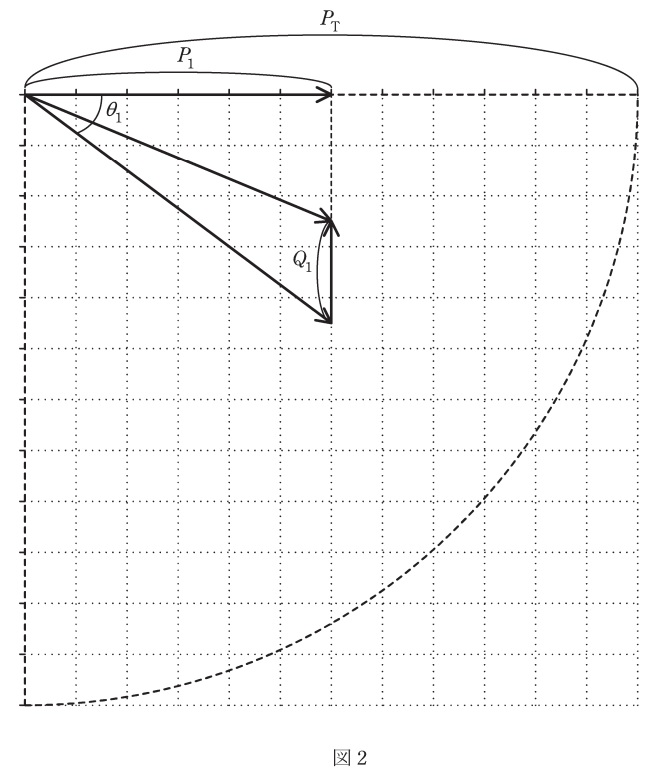
1.有効電力\( \ P \ \)と無効電力\( \ Q \ \)
抵抗で消費される電力を有効電力\( \ P \ \),リアクタンスで消費もしくは供給される電力を無効電力\( \ Q \ \)と呼び,図3のようにベクトル図を描きます。さらに,有効電力\( \ P \ \)と無効電力\( \ Q \ \)のベクトル和は皮相電力\( \ S \ \)と呼ばれ,
\[
\begin{eqnarray}
S&=&\sqrt {P^{2}+Q^{2}} \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。図3において,力率は\( \ \cos \theta \ \)で定義され,
\[
\begin{eqnarray}
\cos \theta &=&\frac {P}{S} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)力率改善用コンデンサの容量\( \ Q_{\mathrm {2}} \ \mathrm {[kvar]} \ \)とそのときの総合力率\( \ \cos \theta _{\mathrm {S}} \ \)
容量\( \ P_{\mathrm {1}}=6 \ 000 \ \mathrm {kW} \ \)で力率\( \ \cos \theta _{\mathrm {1}}=0.8 \ \)(遅れ)の負荷及び容量\( \ P_{\mathrm {2}}=4 \ 500 \ \mathrm {kW} \ \)で力率\( \ \cos \theta _{\mathrm {2}}=0.6 \ \)(遅れ)の負荷の無効電力\( \ Q_{\mathrm {P1}} \ \mathrm {[kvar]} \ \)及び\( \ Q_{\mathrm {P2}} \ \mathrm {[kvar]} \ \)は,ワンポイント解説「2.有効電力\( \ P \ \)と無効電力\( \ Q \ \)」より,
\[
\begin{eqnarray}
Q_{\mathrm {P1}}&=&P_{\mathrm {1}}\tan \theta _{\mathrm {1}} \\[ 5pt ]
&=&P_{\mathrm {1}}\cdot \frac {\sin \theta _{\mathrm {1}}}{\cos \theta _{\mathrm {1}}} \\[ 5pt ]
&=&P_{\mathrm {1}}\cdot \frac {\sqrt {1-\cos ^{2}\theta _{\mathrm {1}}}}{\cos \theta _{\mathrm {1}}} \\[ 5pt ]
&=&6000\times \frac {\sqrt {1-0.8^{2}}}{0.8} \\[ 5pt ]
&=&6000\times \frac {0.6}{0.8} \\[ 5pt ]
&=&4500 \ \mathrm {[kvar]} \\[ 5pt ]
Q_{\mathrm {P2}}&=&P_{\mathrm {2}}\tan \theta _{\mathrm {2}} \\[ 5pt ]
&=&P_{\mathrm {2}}\cdot \frac {\sin \theta _{\mathrm {2}}}{\cos \theta _{\mathrm {2}}} \\[ 5pt ]
&=&P_{\mathrm {2}}\cdot \frac {\sqrt {1-\cos ^{2}\theta _{\mathrm {2}}}}{\cos \theta _{\mathrm {2}}} \\[ 5pt ]
&=&4500\times \frac {\sqrt {1-0.6^{2}}}{0.6} \\[ 5pt ]
&=&4500\times \frac {0.8}{0.6} \\[ 5pt ]
&=&6000 \ \mathrm {[kvar]} \\[ 5pt ]
\end{eqnarray}
\]
となる。変圧器が過負荷にならないためには,接続しているすべての負荷及び力率改善用コンデンサの合計容量が\( \ P_{\mathrm {T}}=12 \ 000 \ \mathrm {kV\cdot A} \ \)よりも小さくならなければならないので,
\[
\begin{eqnarray}
\sqrt {\left( P_{\mathrm {1}}+P_{\mathrm {2}}\right) ^{2}+\left( Q_{\mathrm {P1}}+Q_{\mathrm {P2}}-Q_{\mathrm {1}}-Q_{\mathrm {2}}\right) ^{2}}&=&P_{\mathrm {T}} \\[ 5pt ]
\left( P_{\mathrm {1}}+P_{\mathrm {2}}\right) ^{2}+\left( Q_{\mathrm {P1}}+Q_{\mathrm {P2}}-Q_{\mathrm {1}}-Q_{\mathrm {2}}\right) ^{2}&=&P_{\mathrm {T}}^{2} \\[ 5pt ]
\left( Q_{\mathrm {P1}}+Q_{\mathrm {P2}}-Q_{\mathrm {1}}-Q_{\mathrm {2}}\right) ^{2}&=&P_{\mathrm {T}}^{2}-\left( P_{\mathrm {1}}+P_{\mathrm {2}}\right) ^{2} \\[ 5pt ]
Q_{\mathrm {P1}}+Q_{\mathrm {P2}}-Q_{\mathrm {1}}-Q_{\mathrm {2}}&=&\sqrt {P_{\mathrm {T}}^{2}-\left( P_{\mathrm {1}}+P_{\mathrm {2}}\right) ^{2}} \\[ 5pt ]
Q_{\mathrm {2}}&=&Q_{\mathrm {P1}}+Q_{\mathrm {P2}}-Q_{\mathrm {1}}-\sqrt {P_{\mathrm {T}}^{2}-\left( P_{\mathrm {1}}+P_{\mathrm {2}}\right) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となり,各値を代入すると,
\[
\begin{eqnarray}
Q_{\mathrm {2}}&=&4500+6000-2000-\sqrt {12000^{2}-\left( 6000+4500\right) ^{2}} \\[ 5pt ]
&≒&8500-5809.5 \\[ 5pt ]
&=&2690.5 \ \mathrm {[kvar]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。したがって,過負荷にならないためには,\( \ 2 \ 700 \ \mathrm {[kvar]} \ \)必要となる。また,このときの総合力率\( \ \cos \theta _{\mathrm {S}} \ \)は,皮相電力が変圧器容量\( \ P_{\mathrm {T}}=12 \ 000 \ \mathrm {[kV\cdot A]} \ \)であるから,
\[
\begin{eqnarray}
\cos \theta _{\mathrm {S}}&=&\frac {P_{\mathrm {1}}+P_{\mathrm {2}}}{P_{\mathrm {T}}} \\[ 5pt ]
&=&\frac {6000+4500}{12000} \\[ 5pt ]
&=&0.875 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
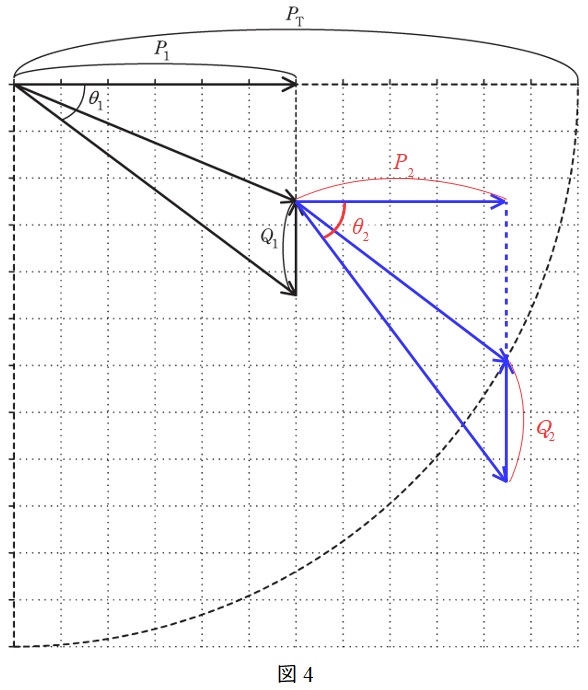
(2)図2に,\( \ P_{\mathrm {2}} \ \mathrm {[kW]} \ \),\( \ Q_{\mathrm {2}} \ \mathrm {[kvar]} \ \)のベクトル図と,力率角\( \ \cos \theta _{\mathrm {2}} \ \)を追記
題意に沿って図2に追記すると,図4のようになる。
最終的に皮相電力が変圧器容量\( \ P_{\mathrm {T}} \ \)(点線)と重なっていることが重要。
(3)総合力率を\( \ \cos \theta _{\mathrm {S}}=0.95 \ \)(遅れ)にするための力率改善用コンデンサの容量\( \ Q_{\mathrm {2}} \ \mathrm {[kvar]} \ \)
総合力率を\( \ \cos \theta _{\mathrm {S}}=0.95 \ \)の時の無効電力\( \ Q_{\mathrm {S}} \ \mathrm {[kvar]} \ \)の大きさは,
\[
\begin{eqnarray}
Q_{\mathrm {S}}&=&\left( P_{\mathrm {1}}+P_{\mathrm {2}}\right) \tan \theta _{\mathrm {S}} \\[ 5pt ]
&=&\left( P_{\mathrm {1}}+P_{\mathrm {2}}\right) \frac {\sin \theta _{\mathrm {S}}}{\cos \theta _{\mathrm {S}}} \\[ 5pt ]
&=&\left( P_{\mathrm {1}}+P_{\mathrm {2}}\right) \frac {\sqrt {1-\cos ^{2}\theta _{\mathrm {S}}}}{\cos \theta _{\mathrm {S}}} \\[ 5pt ]
&=&\left( 6000+4500\right) \times \frac {\sqrt {1-0.95 ^{2}}}{0.95} \\[ 5pt ]
&≒&10500 \times \frac {0.31225}{0.95} \\[ 5pt ]
&≒&3451.2 \ \mathrm {[kvar]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,このときの力率改善用コンデンサの容量\( \ Q_{\mathrm {2}} \ \mathrm {[kvar]} \ \)は,
\[
\begin{eqnarray}
Q_{\mathrm {S}}&=&Q_{\mathrm {P1}}+Q_{\mathrm {P2}}-Q_{\mathrm {1}}-Q_{\mathrm {2}} \\[ 5pt ]
Q_{\mathrm {2}}&=&Q_{\mathrm {P1}}+Q_{\mathrm {P2}}-Q_{\mathrm {1}}-Q_{\mathrm {S}} \\[ 5pt ]
&=&4500+6000-2000-3451.2 \\[ 5pt ]
&=&5048.8 → 5050 \ \mathrm {[kvar]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは