《機械・制御》〈回転機〉[H24:問2]同期発電機の誘導起電力と巻線係数に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

同期発電機の誘導起電力と巻線係数に関して，図を参照して次の問に答えよ。

(1)　同期発電機のコイル辺間隔が磁極間隔に等しく電気角で\( \ \pi \ \mathrm {[rad]} \ \)隔たり（全節巻），かつ，毎極毎相のスロット数が\( \ 1 \ \)（集中巻）の場合，\( \ 1 \ \)相の誘導起電力の実効値\( \ E \ \mathrm {[V]} \ \)を，周波数\( \ f \ \mathrm {[Hz]} \ \)，\( \ 1 \ \)相のコイル直列巻数\( \ n_{\mathrm {c}} \ \)及びコイルと鎖交する磁束の最大値\( \ \mathit {\Phi }_{\mathrm {m}} \ \mathrm {[Wb]} \ \)を用いて表す式を導出せよ。ここで，コイルと鎖交する磁束の瞬時値\( \ \phi \ \mathrm {[Wb]} \ \)は\( \ \phi =\mathit {\Phi }_{\mathrm {m}}\cos \omega t \ \)とする。

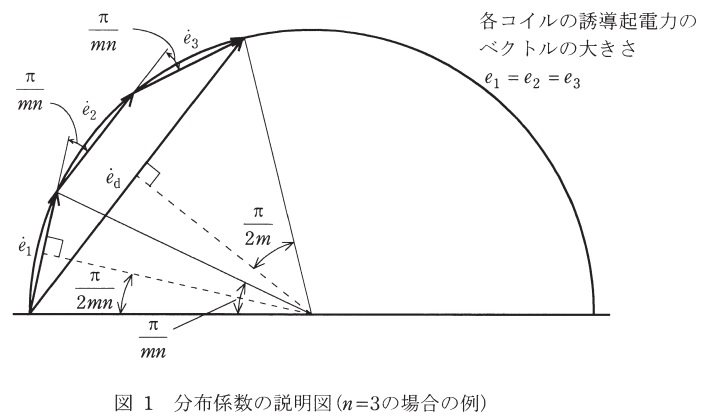
(2)　毎極毎相の導体を\( \ 1 \ \)個のスロットに納めないで，何個かのスロットに分布して配置するのを分布巻という。一般に，毎極毎相のスロット数を\( \ n \ \)，相数を\( \ m \ \)とすれば，各コイル間の誘導起電力の基本波の場合の位相差は\( \ \displaystyle \frac {\pi }{mn} \ \)となり，\( \ n \ \)個のコイルが発生する誘導起電力に関して，そのベクトル和の代数和に対する比を分布係数\( \ K_{\mathrm {d}} \ \)という。図1を参照して，基本波に対する分布係数\( \ K_{\mathrm {d}} \ \)を\( \ m \ \)及び\( \ n \ \)を用いて表す式を導出せよ。また，その算出式を使って，\( \ m=3 \ \)，\( \ n=3 \ \)として，基本波に対する分布係数\( \ K_{\mathrm {d}} \ \)を算出せよ。
　なお，\( \ \displaystyle \sin \frac {\pi }{9}=0.34202 \ \)，\( \ \displaystyle \sin \frac {\pi }{18}=0.17365 \ \)，\( \ \displaystyle \sin \frac {\pi }{27}=0.11609 \ \)とする。

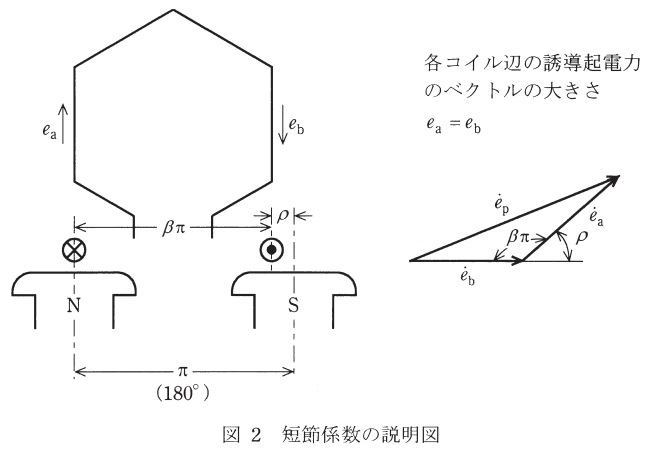
(3)　コイル辺の間隔を磁極間隔より狭いコイルを用いた巻線を短節巻といい，コイル両辺の誘導起電力に位相差が生じ，コイル両辺の誘導起電力のベクトル和がコイル\( \ 1 \ \)個の誘導起電力となり，このベクトル和のコイル両辺の誘導起電力の代数和に対する比を短節係数\( \ K_{\mathrm {p}} \ \)という。図2を参照して，コイル間隔が\( \ \beta \pi \ \mathrm {[rad]} \ \left( \beta ＜1\right) \ \)で，基本波に対する短節係数\( \ K_{\mathrm {p}} \ \)を\( \ \beta \ \)を用いて表す式を導出せよ。また，その算出式を使って，\( \ \displaystyle \beta =\frac {2}{3} \ \)の場合の基本波に対する短節係数\( \ K_{\mathrm {p}} \ \)を算出せよ。

(4)　分布巻で短節巻である巻線の\( \ 1 \ \)相の誘導起電力の実効値\( \ E \ \mathrm {[V]} \ \)を，上記(1)で導出した全節巻及び集中巻の場合の\( \ 1 \ \)相の誘導起電力の実効値の式と分布係数\( \ K_{\mathrm {d}} \ \)と短節係数\( \ K_{\mathrm {p}} \ \)を用いて表す式を導出せよ。また，\( \ f=50 \ \mathrm {[Hz]} \ \)，\( \ n_{\mathrm {c}}=12 \ \)，\( \ \mathit {\Phi }_{\mathrm {m}}=1.5 \ \mathrm {[Wb]} \ \)として，\( \ m=3 \ \)，\( \ n=3 \ \)の基本波に対する\( \ K_{\mathrm {d}} \ \)，及び\( \ \displaystyle \beta =\frac {2}{3} \ \)の場合の基本波に対する\( \ K_{\mathrm {p}} \ \)を代入して，分布巻で短節巻である巻線の\( \ E \ \mathrm {[V]} \ \)を算出せよ。

【ワンポイント解説】

同期発電機の起電力や巻線係数の関係に関する問題です。
電験\( \ 2 \ \)種のテキストではあまり扱われない難易度の高い問題であると思います。一次試験では平成27年の一次試験機械問5で定性的な内容は出題されたことがあります。集中巻や分布巻，全節巻や短節巻の違いといった内容は本問で理解しておくようにしましょう。

1.同期発電機のコイルの巻き方の違い
同期発電機の電機子巻線の巻き方や接続方法には大きく分けて集中巻と分布巻，全節巻と短節巻とに分けられます。

①集中巻と分布巻
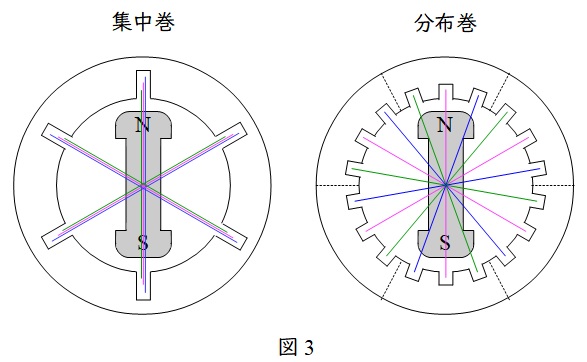
図3のような相数\( \ 3 \ \)の\( \ 2 \ \)極機の同期発電機について考えます。
集中巻は電機子巻線を一つのスロットに集中して巻き付ける巻線方式で，それぞれの起電力の向きが同じ向きであるため大きな起電力が得られることになりますが，奇数次の高調波を含むようになるため，磁束密度の分布が台形に近い形になってしまいます。
一方，分布巻は電機子巻線を複数のスロットに巻き付ける巻線方式で，電機子巻線に発生する誘導起電力の波形を正弦波に近づけることができるようになります。合成の起電力はそれぞれの巻線の起電力の向きが異なるため，それぞれの起電力のベクトル和となり，集中巻と比べて小さくなります。

②全節巻と短節巻
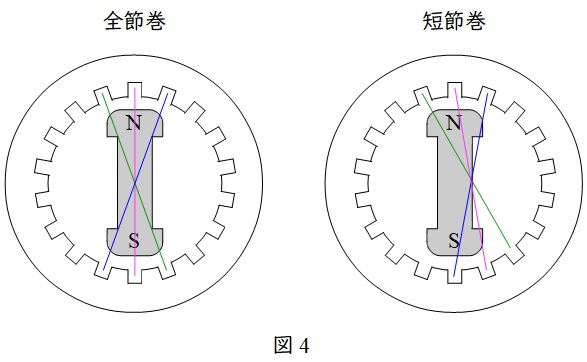
図4のように，\( \ 1 \ \)相分の巻線について，全節巻と短節巻の違いを示します。
全節巻では，コイルの間隔を\( \ \pi \ \mathrm {[rad]} \ \)として，短節巻ではコイルの間隔を\( \ \pi \ \mathrm {[rad]} \ \)より小さくして配置します。
短節巻の方がコイルの起電力は小さくなりますが，電機子巻線に発生する誘導起電力は正弦波に近づけることができるようになります。

【解答】

(1)コイル辺間隔が磁極間隔に等しく電気角で\( \ \pi \ \mathrm {[rad]} \ \)隔たり（全節巻），かつ，毎極毎相のスロット数が\( \ 1 \ \)（集中巻）の場合，\( \ 1 \ \)相の誘導起電力の実効値\( \ E \ \mathrm {[V]} \ \)
\( \ 1 \ \)相あたりの誘導起電力の瞬時値\( \ e \ \mathrm {[V]} \ \)は，コイルと鎖交する磁束の瞬時値\( \ \phi \ \mathrm {[Wb]} \ \)が\( \ \phi =\mathit {\Phi }_{\mathrm {m}}\cos \omega t \ \)であり，全節巻・集中巻の場合の合成起電力はワンポイント解説「1.同期発電機のコイルの巻き方の違い」の通りスカラー和となるので，
\[
\begin{eqnarray}
e &=& -n_{\mathrm {c}}\frac {\mathrm {d}\phi}{\mathrm {d}t} \\[ 5pt ] &=& -n_{\mathrm {c}}\frac {\mathrm {d}}{\mathrm {d}t}\left( \mathit {\Phi }_{\mathrm {m}}\cos \omega t \right) \\[ 5pt ] &=& -n_{\mathrm {c}}\left( -\omega \mathit {\Phi }_{\mathrm {m}}\sin \omega t \right) \\[ 5pt ] &=& 2\pi f n_{\mathrm {c}}\mathit {\Phi }_{\mathrm {m}} \sin \omega t \\[ 5pt ] \end{eqnarray}
\] となる。したがって，その実効値\( \ E \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
E &=& \frac {2\pi f n_{\mathrm {c}}\mathit {\Phi }_{\mathrm {m}}}{\sqrt {2}} \\[ 5pt ] &=& \sqrt {2}\pi f n_{\mathrm {c}}\mathit {\Phi }_{\mathrm {m}} \\[ 5pt ] &≒& 4.4429 f n_{\mathrm {c}}\mathit {\Phi }_{\mathrm {m}}　→　4.44 f n_{\mathrm {c}}\mathit {\Phi }_{\mathrm {m}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)基本波に対する分布係数\( \ K_{\mathrm {d}} \ \)を\( \ m \ \)及び\( \ n \ \)を用いて表す式
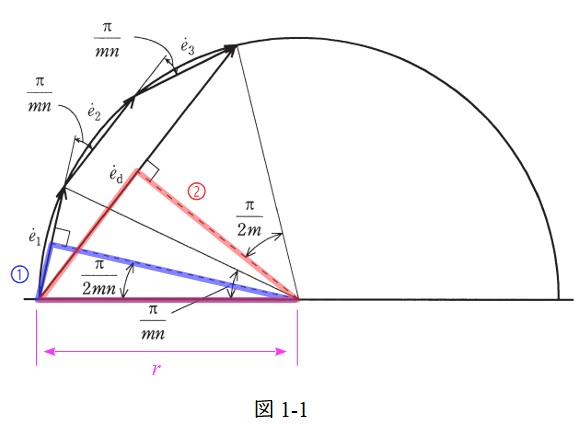
図1-1のように，半径\( \ r \ \)として，①及び②の三角形について考える。また，題意より，\( \ \left| {\dot e}_{1}\right| =\left| {\dot e}_{2}\right| =\left| {\dot e}_{3}\right| =e \ \)とおく。
①の三角形について，
\[
\begin{eqnarray}
\sin \frac {\pi }{2mn} &=& \frac {\displaystyle \frac {e}{2}}{r} \\[ 5pt ] r&=& \frac {e}{\displaystyle 2\sin \frac {\pi }{2mn}} \\[ 5pt ] \end{eqnarray}
\] であり，②の三角形について，
\[
\begin{eqnarray}
\sin \frac {\pi }{2m} &=& \frac {\displaystyle \frac {e_{\mathrm {d}}}{2}}{r} \\[ 5pt ] r&=& \frac {e_{\mathrm {d}}}{\displaystyle 2\sin \frac {\pi }{2m}} \\[ 5pt ] \end{eqnarray}
\] であるから，
\[
\begin{eqnarray}
\frac {e}{\displaystyle 2\sin \frac {\pi }{2mn}}&=& \frac {e_{\mathrm {d}}}{\displaystyle 2\sin \frac {\pi }{2m}} \\[ 5pt ] \frac {e}{\displaystyle \sin \frac {\pi }{2mn}}&=& \frac {e_{\mathrm {d}}}{\displaystyle \sin \frac {\pi }{2m}} \\[ 5pt ] \frac {e_{\mathrm {d}}}{e}&=& \frac {\displaystyle \sin \frac {\pi }{2m}}{\displaystyle \sin \frac {\pi }{2mn}} \\[ 5pt ] \end{eqnarray}
\] となる。\( \ \displaystyle K_{\mathrm {d}}=\frac {e_{\mathrm {d}}}{ne} \ \)であるから，
\[
\begin{eqnarray}
K_{\mathrm {d}}&=& \frac {\displaystyle \sin \frac {\pi }{2m}}{\displaystyle n\sin \frac {\pi }{2mn}} \\[ 5pt ] \end{eqnarray}
\] となり，与えられた数値を代入すると，
\[
\begin{eqnarray}
K_{\mathrm {d}}&=& \frac {\displaystyle \sin \frac {\pi }{2\times 3}}{\displaystyle 3\times \sin \frac {\pi }{2\times 3\times 3}} \\[ 5pt ] &=& \frac {\displaystyle \sin \frac {\pi }{6}}{\displaystyle 3\times \sin \frac {\pi }{18}} \\[ 5pt ] &=& \frac {0.5}{3\times 0.17365} \\[ 5pt ] &≒& 0.95979　→　0.960 \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)基本波に対する短節係数\( \ K_{\mathrm {p}} \ \)を\( \ \beta \ \)を用いて表す式及び\( \ \displaystyle \beta =\frac {2}{3} \ \)の場合の基本波に対する短節係数\( \ K_{\mathrm {p}} \ \)
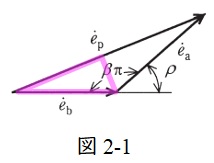
題意より，\( \ \left| {\dot e}_{\mathrm {a}}\right| =\left| {\dot e}_{\mathrm {b}}\right| =e^{\prime } \ \)とおくと，図2-1に示した三角形について，
\[
\begin{eqnarray}
\sin \frac {\beta \pi }{2} &=& \frac {\displaystyle \frac {e_{\mathrm {p}}}{2}}{e^{\prime }} \\[ 5pt ] \frac {e_{\mathrm {p}}}{2e^{\prime }}&=& \sin \frac {\beta \pi }{2} \\[ 5pt ] \end{eqnarray}
\] となり，\( \ \displaystyle K_{\mathrm {p}}=\frac {e_{\mathrm {p}}}{2e^{\prime }} \ \)であるから，
\[
\begin{eqnarray}
K_{\mathrm {p}}&=& \sin \frac {\beta \pi }{2} \\[ 5pt ] \end{eqnarray}
\] と求められる。\( \ \displaystyle \beta =\frac {2}{3} \ \)を代入すると，
\[
\begin{eqnarray}
K_{\mathrm {p}}&=& \sin \frac {\displaystyle \frac {2}{3} \pi }{2} \\[ 5pt ] &=& \sin \frac {\pi }{3} \\[ 5pt ] &≒& 0.86603　→　0.866 \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)分布巻で短節巻である巻線の\( \ 1 \ \)相の誘導起電力の実効値\( \ E \ \mathrm {[V]} \ \)
(1)～(3)より，分布巻で短節巻である巻線の\( \ 1 \ \)相の誘導起電力の実効値\( \ E \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
E&=& 4.4429 f n_{\mathrm {c}}\mathit {\Phi }_{\mathrm {m}}K_{\mathrm {d}}K_{\mathrm {p}}　→　4.44 f n_{\mathrm {c}}\mathit {\Phi }_{\mathrm {m}}K_{\mathrm {d}}K_{\mathrm {p}} \\[ 5pt ] \end{eqnarray}
\] となり，各値を代入すると，
\[
\begin{eqnarray}
E&=& 4.4429 \times 50 \times 12 \times 1.5 \times 0.95979 \times 0.86603 \\[ 5pt ] &≒& 3323.6　→　3320 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。