《電力・管理》〈水力〉[H21:問1]水車の出力と有効落差の関係に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

水車の案内羽根開度及び効率を一定とした場合に，次の問に答えよ。

(1)　水車の出力\( \ P \ \mathrm {[kW]} \ \)は有効落差\( \ H \ \mathrm {[m]} \ \)の関数として表されるが，その関係を次に示す諸量を表す記号を用いて式で表せ。

水車効率を\( \ \eta \ \mathrm {[％]} \ \)，水圧管の断面積を\( \ A \ \mathrm {[m^{2}]} \ \)，重力加速度を\( \ g \ \mathrm {[m / s^{2}]} \ \)，管路損失等による流速の低下を考慮した流速係数を\( \ k \ \ \)として用いること。

(2)　(1)を用いて，有効落差\( \ 100 \ \mathrm {[m]} \ \)，最大出力\( \ 8 \ 000 \ \mathrm {[kW]} \ \)の水力発電所が水位変化によって有効落差が\( \ 81 \ \mathrm {[m]} \ \)に低下したときの最大出力を求めよ。

【ワンポイント解説】

水力発電所の水車出力と有効落差の関係を求める問題です。
\( \ 2 \ \)種の二次受験生ですと，多くの方は公式は理解していると思いますが，その中でその公式をどのように扱うかを問われています。慣れの面もありますので，本問でしっかりと理解しておくようにして下さい。

1.断面積\( \ A \ \mathrm {[m^{2}]} \ \)と流速\( \ v \ \mathrm {[m / s ]} \ \)と流量\( \ Q \ \mathrm {[m^{3} / s ]} \ \)の関係
断面積\( \ A \ \mathrm {[m^{2}]} \ \)の配管内を流速\( \ v \ \mathrm {[m / s ]} \ \)で水が流れている時，配管内を流れる水の流量\( \ Q \ \mathrm {[m^{3} / s ]} \ \)は，
\[
\begin{eqnarray}
Q&=&Av \\[ 5pt ] \end{eqnarray}
\] となります。

2.ベルヌーイの定理
水の持つエネルギーを水柱の高さに置き換えたものを水頭といい，位置水頭が\( \ h \ \)，圧力水頭が\( \ \displaystyle \frac {p}{\rho g} \ \)，速度水頭が\( \ \displaystyle \frac {v^{2}}{2g} \ \)で表されるとき，これらの総和はエネルギー保存則によりどの場所でも等しくなり，これをベルヌーイの定理といいます。
\[
\begin{eqnarray}
h+\frac {p}{\rho g}+\frac {v^{2}}{2g}&=&一定 \\[ 5pt ] \end{eqnarray}
\]

3.水力発電所の出力\( \ P \ \mathrm {[kW]} \ \)
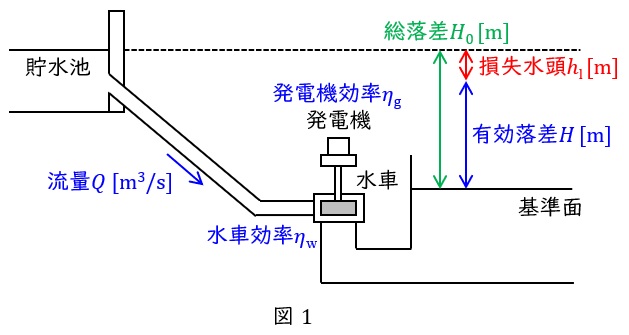
水力発電所の使用水量\( \ Q \ \mathrm {[m^{3}／s]} \ \)，有効落差\( \ H \ \mathrm {[m]} \ \)，水車効率\( \ \eta _{\mathrm {w}} \ \)，発電機効率\( \ \eta _{\mathrm {g}} \ \)とすると，発電機の出力\( \ P \ \mathrm {[kW]} \ \)は，重力加速度\( \ 9.8 \ \mathrm {m / s^{2}} \ \)及び水の密度\( \ 1 \ 000 \ \mathrm {kg / m^{3}} \ \)を考慮すると，
\[
\begin{eqnarray}
P &=&9.8QH\eta _{\mathrm {w}}\eta _{\mathrm {g}} \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] で求められます。

【解答】

(1)水車の出力\( \ P \ \mathrm {[kW]} \ \)を有効落差\( \ H \ \mathrm {[m]} \ \)の関数として表す
水車入口の流速を\( \ v \ \mathrm {[m / s]} \ \)とすると，有効落差がすべて速度水頭に変化したと考えれば，ワンポイント解説「2.ベルヌーイの定理」の通り，
\[
\begin{eqnarray}
H&=&\frac {v^{2}}{2g} \\[ 5pt ] v^{2}&=&2gH \\[ 5pt ] v&=&\sqrt {2gH} \\[ 5pt ] \end{eqnarray}
\] となり，流速係数\( \ k \ \)を考慮すると，
\[
\begin{eqnarray}
v&=&k\sqrt {2gH} \\[ 5pt ] \end{eqnarray}
\] となる。よって，水圧管内の流量\( \ Q \ \mathrm {[m^{3}／s]} \ \)は，ワンポイント解説「1.断面積\( \ A \ \mathrm {[m^{2}]} \ \)と流速\( \ v \ \mathrm {[m / s ]} \ \)と流量\( \ Q \ \mathrm {[m^{3} / s ]} \ \)の関係」の通り，
\[
\begin{eqnarray}
Q&=&Av \\[ 5pt ] &=&Ak\sqrt {2gH} \\[ 5pt ] \end{eqnarray}
\] となる。以上から，水車の出力\( \ P \ \mathrm {[kW]} \ \)は，ワンポイント解説「3.水力発電所の出力\( \ P \ \mathrm {[kW]} \ \)」の通り，
\[
\begin{eqnarray}
P &=&gQH\frac {\eta }{100} \\[ 5pt ] &=&gAk\sqrt {2gH}\cdot H\frac {\eta }{100} \\[ 5pt ] &=&\sqrt {2}Akg^{\frac {3}{2}}H^{\frac {3}{2}}\frac {\eta }{100} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)有効落差が\( \ 81 \ \mathrm {[m]} \ \)に低下したときの最大出力
(1)解答式より，\( \ P∝H^{\frac {3}{2}} \ \)であるから，有効落差\( \ H_{1}=100 \ \mathrm {[m]} \ \)，最大出力\( \ P_{1}=8 \ 000 \ \mathrm {[kW]} \ \)から有効落差が\( \ H_{2}=81 \ \mathrm {[m]} \ \)に低下したときの最大出力\( \ P_{2} \ \mathrm {[kW]} \ \)は，
\[
\begin{eqnarray}
\frac {P_{2}}{P_{1}} &=&\frac {H_{2}^{\frac {3}{2}}}{H_{1}^{\frac {3}{2}}} \\[ 5pt ] P_{2}&=&\left( \frac {H_{2}}{H_{1}}\right) ^{\frac {3}{2}}P_{1} \\[ 5pt ] &=&\left( \frac {81}{100}\right) ^{\frac {3}{2}}\times 8 \ 000 \\[ 5pt ] &≒&5 \ 830 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。