《電力・管理》〈送電〉[H25:問2]対地静電容量に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

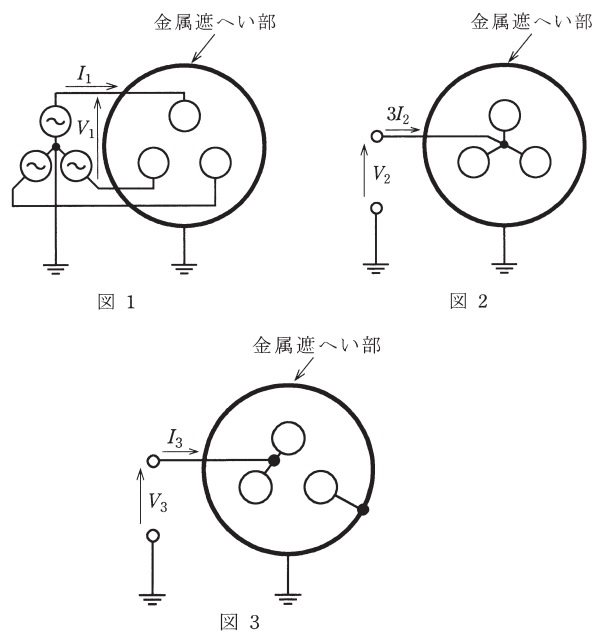
図1に示すように，無負荷の三心ケーブルの金属遮へい部を接地して\( \ 3 \ \)本の導体に周波数\( \ f \ \mathrm {[Hz]} \ \)の三相平衡電圧(線間電圧)\( \ V_{1} \ \mathrm {[V]} \ \)を加えたときに各導体に流れる電流を\( \ I_{1} \ \mathrm {[A]} \ \)とする。また，図2に示すように，全ての導体を接続して周波数\( \ f \ \mathrm {[Hz]} \ \)の交流電圧\( \ V_{2} \ \mathrm {[V]} \ \)を加えたときに各導体に流れる電流を\( \ I_{2} \ \mathrm {[A]} \ \)とする。このケーブルについて次の問に答えよ。ただし，導体相互間の静電容量は等しく，各導体と金属遮へい部間の静電容量も等しいものとする。また，各導体の抵抗，インダクタンスは無視する。

(1)　導体相互間の静電容量\( \ C_{\mathrm {m}} \ \mathrm {[F]} \ \)，及び各導体と金属遮へい間の静電容量\( \ C_{\mathrm {o}} \ \mathrm {[F]} \ \)をそれぞれ求めよ。

(2)　このケーブルを図3のように接続して周波数\( \ 5f \ \mathrm {[Hz]} \ \)の交流電圧\( \ V_{3} \ \mathrm {[V]} \ \)を加えた。流れる電流\( \ I_{3} \ \mathrm {[A]} \ \)を\( \ I_{1} \ \mathrm {[A]} \ \)，\( \ I_{2} \ \mathrm {[A]} \ \)，\( \ V_{1} \ \mathrm {[V]} \ \)，\( \ V_{2} \ \mathrm {[V]} \ \)，\( \ V_{3} \ \mathrm {[V]} \ \)を用いて求めよ。

【ワンポイント解説】

3種の頃から何度も出題されてきたような内容ではありますが，図1では三相交流である一方図2では単相となっていたり，図2では\( \ 3I_{2} \ \)となっていたり，(2)では周波数が\( \ 5 \ \)倍となっていたりする等，落とし穴の多い問題と言えます。ミスに注意して解くようにしましょう。

1.ケーブルの静電容量\( \ C \ \)
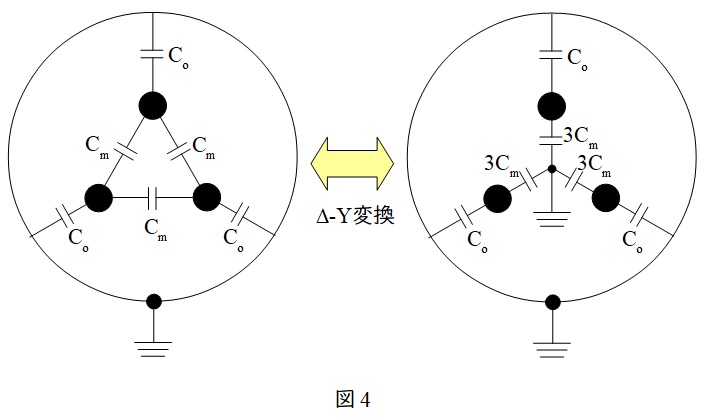
図4の通り対地静電容量\( \ C_{\mathrm {o}} \ [\mathrm {F}] \ \)，線間静電容量\( \ C_{\mathrm {m}} \ [\mathrm {F}] \ \)とすると，\( \ C_{\mathrm {m}} \ [\mathrm {F}] \ \)は\( \ \Delta -\mathrm {Y} \ \)変換により\( \ 3C_{\mathrm {m}} \ \)の\( \ \mathrm {Y} \ \)回路に変換できます。中性点の電位は\( \ 0 \ \)であるから，\( \ 3C_{\mathrm {m}} \ \)と\( \ C_{\mathrm {o}} \ \)は並列となるため，\( \ 1 \ \)相あたりの静電容量\( \ C \ \)は，
\[
\begin{eqnarray}
C&=&C_{\mathrm {o}}+3C_{\mathrm {m}} \\[ 5pt ] \end{eqnarray}
\] となります。

2.ケーブルの充電電流\( \ I_{\mathrm {C}} \ \)
ケーブル\( \ 1 \ \)相あたりの静電容量\( \ C \ \)，三相交流の線間電圧\( \ V \ \)とすると，ケーブルの充電電流\( \ I_{\mathrm {C}} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {C}}&=&\frac {\displaystyle \frac {V}{\sqrt {3}}}{\displaystyle \frac {1}{\omega C}} \\[ 5pt ] &=&\frac {\omega CV}{\sqrt {3}} \\[ 5pt ] &=&\frac {2\pi fCV}{\sqrt {3}} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)導体相互間の静電容量\( \ C_{\mathrm {m}} \ \mathrm {[F]} \ \)，及び各導体と金属遮へい間の静電容量\( \ C_{\mathrm {o}} \ \mathrm {[F]} \ \)
図1において，ワンポイント解説「1.ケーブルの静電容量\( \ C \ \)」の通り，\( \ 1 \ \)相あたりの作用静電容量\( \ C_{1} \ \)は，
\[
\begin{eqnarray}
C_{1}&=&C_{\mathrm {o}}+3C_{\mathrm {m}} \\[ 5pt ] \end{eqnarray}
\] となる。ワンポイント解説「2.ケーブルの充電電流\( \ I_{\mathrm {C}} \ \)」の通り，ケーブルの充電電流\( \ I_{1} \ \)は，
\[
\begin{eqnarray}
I_{1}&=&\frac {2\pi fC_{1}V_{1}}{\sqrt {3}} \\[ 5pt ] &=&\frac {2\pi f\left( C_{\mathrm {o}}+3C_{\mathrm {m}}\right) V_{1}}{\sqrt {3}}　・・・・・・・・・・　① \\[ 5pt ] \end{eqnarray}
\] となる。次に，図2において，三相一括にして短絡しているので，図2における静電容量\( \ C_{2} \ \)は，
\[
\begin{eqnarray}
C_{2}&=&3C_{\mathrm {o}} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，ケーブルの充電電流\( \ I_{2} \ \)は，
\[
\begin{eqnarray}
3I_{2}&=&2\pi fC_{2}V_{2} \\[ 5pt ] &=&6\pi fC_{\mathrm {o}}V_{2} \\[ 5pt ] I_{2}&=&2\pi fC_{\mathrm {o}}V_{2} \\[ 5pt ] \end{eqnarray}
\] となり，これよりケーブルの対地静電容量\( \ C_{\mathrm {o}} \ \)は，
\[
\begin{eqnarray}
C_{\mathrm {o}}&=&\frac {I_{2}}{2\pi fV_{2}} \\[ 5pt ] \end{eqnarray}
\] と求められる。これを①に代入して\( \ C_{\mathrm {m}} \ \)を求めると，
\[
\begin{eqnarray}
I_{1}&=&\frac {\displaystyle 2\pi f\left( \frac {I_{2}}{2\pi fV_{2}}+3C_{\mathrm {m}}\right) V_{1}}{\sqrt {3}} \\[ 5pt ] \frac {I_{2}}{2\pi fV_{2}}+3C_{\mathrm {m}}&=&\frac {\sqrt {3}I_{1}}{2\pi fV_{1}} \\[ 5pt ] 3C_{\mathrm {m}}&=&\frac {\sqrt {3}I_{1}}{2\pi fV_{1}}-\frac {I_{2}}{2\pi fV_{2}} \\[ 5pt ] C_{\mathrm {m}}&=&\frac {1}{6\pi f}\left( \frac {\sqrt {3}I_{1}}{V_{1}}-\frac {I_{2}}{V_{2}}\right) \\[ 5pt ] \end{eqnarray}
\] と求められる。

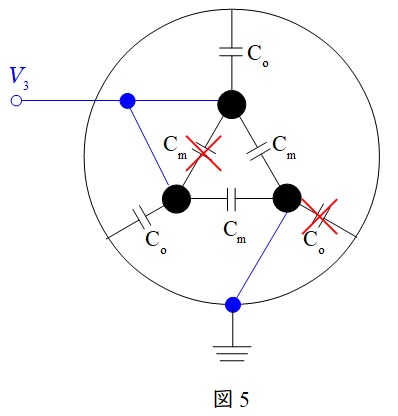
(2)図3のように接続して周波数\( \ 5f \ \mathrm {[Hz]} \ \)の交流電圧\( \ V_{3} \ \mathrm {[V]} \ \)を加えた時に流れる電流\( \ I_{3} \ \mathrm {[A]} \ \)
図3のように接続すると，回路としては図5のように構成される。図5において，回路は\( \ C_{\mathrm {o}} \ \)及び\( \ C_{\mathrm {m}} \ \)を二つずつすべて並列に接続したものであるから，ケーブルの充電電流\( \ I_{3} \ \)は，
\[
\begin{eqnarray}
I_{3}&=&2\pi \cdot 5f\left( 2C_{\mathrm {o}}+2C_{\mathrm {m}}\right) V_{3} \\[ 5pt ] &=&20\pi f\left( C_{\mathrm {o}}+C_{\mathrm {m}}\right) V_{3} \\[ 5pt ] &=&20\pi f\left[ \frac {I_{2}}{2\pi fV_{2}}+\frac {1}{6\pi f}\left( \frac {\sqrt {3}I_{1}}{V_{1}}-\frac {I_{2}}{V_{2}}\right) \right] V_{3} \\[ 5pt ] &=&10\left[ \frac {I_{2}}{V_{2}}+\frac {1}{3}\left( \frac {\sqrt {3}I_{1}}{V_{1}}-\frac {I_{2}}{V_{2}}\right) \right] V_{3} \\[ 5pt ] &=&\frac {10}{3}\left( \frac {\sqrt {3}I_{1}}{V_{1}}+\frac {2I_{2}}{V_{2}}\right) V_{3} \\[ 5pt ] \end{eqnarray}
\] と求められる。