《電力・管理》〈配電〉[H28:問6]パーセントインピーダンスに関する計算問題

【問題】

【難易度】★★★☆☆（普通）

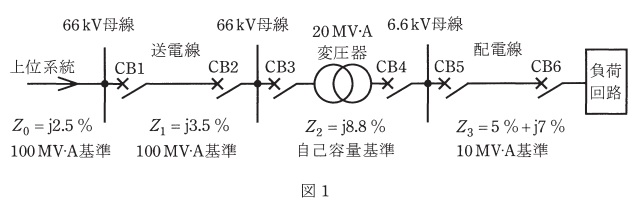
図1は，送電線から受電した\( \ \mathrm {66 \ kV} \ \)を\( \ \mathrm {20 \ MV\cdot A} \ \)変圧器で降圧して\( \ \mathrm {6.6 \ kV} \ \)負荷回路に供給する回路である。\( \ Z_{0}～Z_{3} \ \)がそれぞれの送電線路，配電線路における区分ごとの合成インピーダンスを表すとき，次の問に答えよ。ただし，上位系統の背後電圧を\( \ \mathrm {66 \ kV} \ \)一定とし，負荷回路からの短絡電流供給はないものとする。

(1)　\( \ \mathrm {66 \ kV} \ \)\(\mathrm {CB3} \ \)から見た電源側背後インピーダンスの大きさ\( \ \mathrm { [ \Omega ] } \ \)を求めよ。
(2)　\( \ \mathrm {66 \ kV} \ \)\(\mathrm {CB3} \ \)における三相短絡電流\( \ \mathrm { [ kA ] } \ \)を求めよ。
(3)　\( \ \mathrm {6.6 \ kV} \ \)\(\mathrm {CB6} \ \)における三相短絡電流\( \ \mathrm { [ kA ] } \ \)を求めよ。
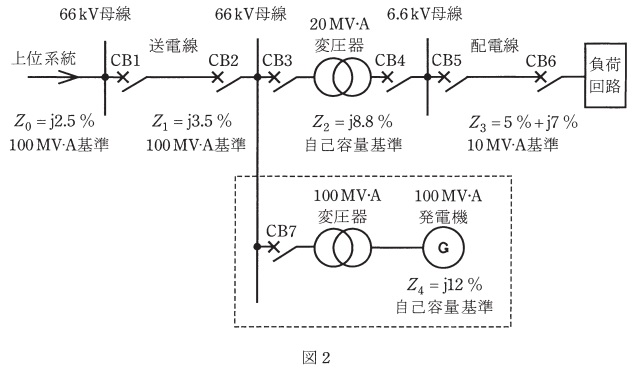
(4)　\( \ \mathrm {100 \ MV\cdot A} \ \)の発電機(初期過渡リアクタンス\( \ Z_{4}=\mathrm {j}12 \ ％ \ \) )を図2のように\( \ \mathrm {66 \ kV} \ \)母線に接続することとした。\( \ \mathrm {CB2} \ \)，\( \ \mathrm {CB3} \ \)及び\( \ \mathrm {CB7} \ \)の定格遮断電流が\( \ \mathrm {20 \ kA} \ \)であるとき，\( \ \mathrm {100 \ MV\cdot A} \ \)変圧器の自己容量基準パーセントインピーダンスの下限値\( \ \mathrm { [ ％ ] } \ \)を求めよ。

【ワンポイント解説】

典型的なパーセントインピーダンスに関する問題で，パーセントインピーダンスの概念を理解し，過去問をこなしていれば問題なく解けると思います。

1.パーセントインピーダンスの基本式
\[
\begin{eqnarray}
％Z&=&\frac {\sqrt {3}ZI_{\mathrm {n}}}{V_{\mathrm {n}}}\times 100 [ ％ ] 　(定義) \\[ 5pt ] &=& \frac {\sqrt {3}ZV_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}}\times 100 　←分母分子にV_{\mathrm {n}}を掛ける \\[ 5pt ] &=& \frac {P_{\mathrm {n}}Z}{V_{\mathrm {n}}^{2}}\times 100　←P_{\mathrm {n}}=\sqrt{3} V_{\mathrm {n}}I_{\mathrm {n}}
\end{eqnarray}
\]

2.パーセントインピーダンスの容量変換
上記1よりパーセントインピーダンスは基準容量に比例するので基準容量\(P_{\mathrm {A}}\)の時のパーセントインピーダンスが\(％Z_{\mathrm {A}}\)であるとき，基準容量\(P_{\mathrm {B}}\)に変換した際のパーセントインピーダンスは\(％Z_{\mathrm {B}}\)は
\[
％Z_{\mathrm {B}}=\frac {P_{\mathrm {B}}}{P_{\mathrm {A}}}％Z_{\mathrm {A}}
\] となります。

3.三相短絡電流\(I_{S}\)の導出
相電圧\(\displaystyle E_{\mathrm {n}}=\frac {V_{\mathrm {n}}}{\sqrt{3}}\)であり，短絡電流\(\displaystyle I_{\mathrm {S}}=\frac {E_{\mathrm {n}}}{Z}\)であるから，
\[
\begin{eqnarray}
I_{\mathrm {S}}&=&\frac {E_{\mathrm {n}}}{Z} \\[ 5pt ] &=& \frac {E_{\mathrm {n}}}{\displaystyle ％Z\cdot \frac {E_{\mathrm {n}}}{I_{\mathrm {n}}\times 100}} \\[ 5pt ] &=& \frac {I_{\mathrm {n}}}{％Z}\times 100
\end{eqnarray}
\] となります。

【解答】

(1)\( \ \mathrm {66 \ kV} \ \)\(\mathrm {CB3} \ \)から見た電源側背後インピーダンスの大きさ\( \ \mathrm { [ \Omega ] } \ \)
\(\mathrm {CB3}\)から見た電源側背後パーセントインピーダンス\(％Z_{\mathrm {A}}\)の大きさは，
\[
\begin{eqnarray}
％Z_{\mathrm {A}}&=&％Z_{0}+％Z_{1} \\[ 5pt ] &=& 2.5+ 3.5 \\[ 5pt ] &=& 6 \ [ ％ ] \end{eqnarray}
\] であるから、ワンポイント解説「1.パーセントインピーダンスの基本式」より\(\mathrm {CB3}\)から見た電源側背後インピーダンス\(Z_{\mathrm {A}}\)の大きさは，
\[
\begin{eqnarray}
％Z_{\mathrm {A}}&=&\frac {P_{\mathrm {n}}Z_{\mathrm {A}}}{V_{\mathrm {n}}^{2}}\times 100 \\[ 5pt ] Z_{\mathrm {A}}&=& \frac {％Z_{\mathrm {A}}V_{\mathrm {n}}^{2}}{P_{\mathrm {n}}\times 100} \\[ 5pt ] &=& \frac {6\times \left( 66\times 10^{3}\right) ^{2}}{100\times 10^{6}\times 100} \\[ 5pt ] &≒& 2.6136　→　2.61 \ [ \Omega ] \end{eqnarray}
\] と求められる。

(2)\( \ \mathrm {66 \ kV} \ \)\(\mathrm {CB3} \ \)における三相短絡電流\( \ \mathrm { [ kA ] } \ \)
\(P_{\mathrm {n}}=\sqrt {3} V_{\mathrm {n}}I_{\mathrm {n}}\)より，基準電流\(I_{\mathrm {n}}\)は，
\[
\begin{eqnarray}
I_{\mathrm {n}}&=&\frac {P_{\mathrm {n}}}{\sqrt {3} V_{\mathrm {n}}} \\[ 5pt ] &=& \frac {100\times 10^{6}}{\sqrt {3}\times 66\times 10^{3}} \\[ 5pt ] &≒& 874.77 \ [ \mathrm {A} ] \end{eqnarray}
\] となるので，\(\mathrm {CB3}\)における三相短絡電流\(I_{\mathrm {S3}}\)は，ワンポイント解説「3.三相短絡電流\(I_{\mathrm {S}}\)の導出」より，
\[
\begin{eqnarray}
I_{\mathrm {S3}}&=&\frac {I_{\mathrm {n}}}{％Z_{\mathrm {A}}}\times 100 \\[ 5pt ] &=& \frac {874.77}{6}\times 100 \\[ 5pt ] &≒& 14579.5 \ [ \mathrm {A} ]　→　14.6 \ [ \mathrm {kA} ] \end{eqnarray}
\] と求められる。

(3)\( \ \mathrm {6.6 \ kV} \ \)\(\mathrm {CB6} \ \)における三相短絡電流\( \ \mathrm { [ kA ] } \ \)
ワンポイント解説「2.パーセントインピーダンスの容量変換」より\( \ Z_{2} \ \)及び\( \ Z_{3} \ \)を\( \ 100 \ \mathrm {MV\cdot A} \ \)容量ベースに変換すると，
\[
\begin{eqnarray}
％Z_{2}&=&\frac {100}{20}\times \mathrm {j}8.8 &=& \mathrm {j}44 \ [ ％ ] \\[ 5pt ] ％Z_{3}&=&\frac {100}{10}\times \left( 5 +\mathrm {j} 7 \right) &=& 50+\mathrm {j}70 \ [ ％ ] \end{eqnarray}
\] となるから，\( \ \mathrm {CB6} \ \)から見た電源側背後インピーダンス\( \ ％Z_{\mathrm {B}} \ \)は，
\[
\begin{eqnarray}
％Z_{\mathrm {B}}&=&％Z_{0}+％Z_{1}+％Z_{2}+％Z_{3} \\[ 5pt ] &=&\mathrm {j}2.5+\mathrm {j}3.5+\mathrm {j}44 +50+\mathrm {j}70 \\[ 5pt ] &=&50+\mathrm {j}120 \ [ ％ ] \end{eqnarray}
\] となる。また，\( \ \mathrm {CB6} \ \)での基準電流\( \ I_{\mathrm {n}} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {n}}&=&\frac {P_{\mathrm {n}}}{\sqrt {3} V_{\mathrm {n}}} \\[ 5pt ] &=& \frac {100\times 10^{6}}{\sqrt {3}\times 6.6\times 10^{3}} \\[ 5pt ] &≒& 8747.7 \ [ \mathrm {A} ] \end{eqnarray}
\] であるから，\( \ \mathrm {CB6} \ \)における三相短絡電流\( \ I_{\mathrm {S6}} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {S6}}&=&\frac {I_{\mathrm {n}}}{％Z_{\mathrm {B}}}\times 100 \\[ 5pt ] &=& \frac {8747.7}{\sqrt {50^{2}+120^{2}}}\times 100 \\[ 5pt ] &=& 6729 \ [ \mathrm {A} ]　→　6.73 \ [ \mathrm {kA} ] \end{eqnarray}
\] と求められる。

(4)\( \ \mathrm {100 \ MV\cdot A} \ \)変圧器の自己容量基準パーセントインピーダンスの下限値\( \ \mathrm { [ ％ ] } \ \)
定格遮断電流が等しい\( \ \mathrm {CB2} \ \)，\( \ \mathrm {CB3} \ \)，\( \ \mathrm {CB7} \ \)のうち，\( \ \mathrm {CB2} \ \)は本設問と関係なく，\( \ \mathrm {CB7} \ \)は\( \ \mathrm {CB3} \ \)より遮断電流が小さくなる。よって本問は\( \ \mathrm {CB3} \ \)が条件を満たせばよい。ここで，(2)より，\( \ \mathrm {CB3} \ \)における三相短絡電流\( \ I_{\mathrm {S3}} \ \)は\( \ \mathrm {14579.5 \ [ A ]} \ \)なので，新たに接続する発電機による定格遮断電流\( \ I_{\mathrm {S7}} \ \)は，
\[
I_{\mathrm {S7}}=20000-14579.5 =5420.5 \ [\mathrm {A}] \] 以下となればよい。よって，変圧器のパーセントインピーダンスを\( \ ％Z_{\mathrm {T}} \ \)とすると，
\[
\begin{eqnarray}
I_{\mathrm {S7}}&=&\frac {I_{\mathrm {n}}}{％Z_{\mathrm {T}}+％Z_{4}}\times 100 \\[ 5pt ] 5420.5&=&\frac {874.77}{％Z_{\mathrm {T}}+12}\times 100 \\[ 5pt ] ％Z_{\mathrm {T}}&≒& 4.14 \ [ ％ ] \end{eqnarray}
\] と求められる。