【問題】
【難易度】★★★★★(難しい)
対称座標法を用いた\( \ 1 \ \)線地絡故障の計算に関して,次の問に答えよ。
図のような送受電端の変圧器の中性点をそれぞれ\( \ R_{\mathrm {e}} \ \)の抵抗で接地したこう長\( \ 20 \ \mathrm {km} \ \),電圧\( \ 66 \ \mathrm {kV} \ \),周波数\( \ 50 \ \mathrm {Hz} \ \)の三相\( \ 3 \ \)線式\( \ 1 \ \)回線送電線路がある。
その\( \ \mathrm {a} \ \)相\( \ 1 \ \)線が\( \ R_{\mathrm {f}} \ \)の抵抗を通じて地絡を生じた場合の地絡電流を求めたい。
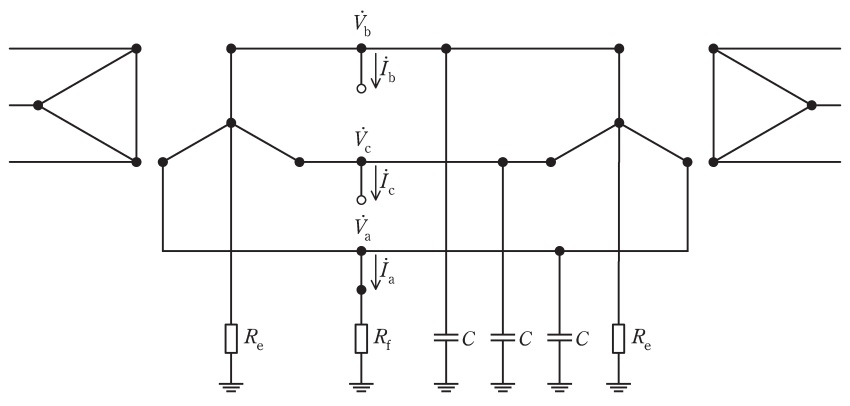
(1) 地絡電流\( \ {\dot I}_{\mathrm {g}} \ \)を,\( \ \mathrm {a} \ \)相の無負荷電圧\( \ {\dot E}_{\mathrm {a}} \ \),この送電回路の故障点から見た零相インピーダンス\( \ {\dot Z}_{\mathrm {0}} \ \),正相インピーダンス\( \ {\dot Z}_{\mathrm {1}} \ \),逆相インピーダンス\( \ {\dot Z}_{\mathrm {2}} \ \),及び,地絡点の抵抗\( \ R_{\mathrm {f}} \ \)で表せ。
なお,故障点での各相電圧,各相電流を図に示すように\( \ {\dot V}_{\mathrm {a}} \ \),\( \ {\dot V}_{\mathrm {b}} \ \),\( \ {\dot V}_{\mathrm {c}} \ \),\( \ {\dot I}_{\mathrm {a}} \ \),\( \ {\dot I}_{\mathrm {b}} \ \),\( \ {\dot I}_{\mathrm {c}} \ \)とし,それを対称成分に変換したものを\( \ {\dot V}_{\mathrm {0}} \ \),\( \ {\dot V}_{\mathrm {1}} \ \),\( \ {\dot V}_{\mathrm {2}} \ \),\( \ {\dot I}_{\mathrm {0}} \ \),\( \ {\dot I}_{\mathrm {1}} \ \),\( \ {\dot I}_{\mathrm {2}} \ \)としたとき,以下の関係となる。
\[
\begin{eqnarray}
{\dot V}_{\mathrm {0}}&=&-{\dot Z}_{\mathrm {0}}{\dot I}_{\mathrm {0}},{\dot V}_{\mathrm {1}}&=&{\dot E}_{\mathrm {a}}-{\dot Z}_{\mathrm {1}}{\dot I}_{\mathrm {1}},{\dot V}_{\mathrm {2}}&=&-{\dot Z}_{\mathrm {2}}{\dot I}_{\mathrm {2}} \\[ 5pt ]
\end{eqnarray}
\]
また,故障条件から以下の関係となる。
\[
\begin{eqnarray}
{\dot I}_{\mathrm {b}}&=&{\dot I}_{\mathrm {c}}&=&0,{\dot V}_{\mathrm {a}}&=&{\dot I}_{\mathrm {a}}R_{\mathrm {f}} \\[ 5pt ]
\end{eqnarray}
\]
(2)零相インピーダンス\( \ {\dot Z}_{\mathrm {0}} \ \),正相インピーダンス\( \ {\dot Z}_{\mathrm {1}} \ \),逆相インピーダンス\( \ {\dot Z}_{\mathrm {2}} \ \)をそれぞれ求めよ。ただし,\( \ 1 \ \)線当たりの対地静電容量\( \ C \ \)は\( \ 0.005 \ \mathrm {\mu F /km} \ \),変圧器の中性点の抵抗\( \ R_{\mathrm {e}} \ \)は\( \ \displaystyle \frac {2000}{3} \ \mathrm {\Omega } \ \)として,その他のインピーダンス,また負荷電流は無視するものとする。
なお,\( \ \pi =3.1416 \ \)とする。
(3)小問(2)の条件に加えて,地絡点の抵抗\( \ R_{\mathrm {f}} \ \)が\( \ \displaystyle 10 \ \mathrm {\Omega } \ \)の場合における地絡電流の大きさ\( \ \left| {\dot I}_{\mathrm {g}}\right| \ \mathrm {[A]} \ \)を求めよ。
【ワンポイント解説】
\( \ 1 \ \)種では定番の対称座標法を用いた計算が\( \ 2 \ \)種でも久しぶりに出題された印象の問題です。
対称座標法は対称座標の考え方で決まる定義的な内容なので覚えておく必要がありますが,覚えてしまうと比較的パターン化されている問題でもあります。
計算量も非常に多く少しハードル高く感じるかもしれませんが,何回か演習を繰り返し問題に慣れ解けるようになりましょう。
1.ベクトルオペレータ\( \ a \ \)
ベクトルオペレータとは,\( \ a=\mathrm {e}^{\mathrm {j}\frac {2\pi}{3}} \ \)で定義される演算子であり,
\[
\begin{eqnarray}
a &=& \cos \frac {2\pi}{3}+\mathrm {j}\sin \frac {2\pi}{3} \\[ 5pt ]
&=& -\frac {1}{2}+\mathrm {j}\frac {\sqrt {3}}{2} \\[ 5pt ]
a^{2} &=& \cos \frac {4\pi}{3}+\mathrm {j}\sin \frac {4\pi}{3} \\[ 5pt ]
&=& -\frac {1}{2}-\mathrm {j}\frac {\sqrt {3}}{2} \\[ 5pt ]
a^{3} &=& \cos \frac {6\pi}{3}+\mathrm {j}\sin \frac {6\pi}{3} \\[ 5pt ]
&=& 1 \\[ 5pt ]
\end{eqnarray}
\]
という関係があります。
2.対称座標法
故障計算をする際に,非常に便利な方法で,以下のように定義されます。
零相電圧\( \ {\dot V}_{0} \ \),正相電圧\( \ {\dot V}_{1} \ \),逆相電圧\( \ {\dot V}_{2} \ \)とすると,各相の電圧\( \ {\dot V}_{\mathrm {a}} \ \),\( \ {\dot V}_{\mathrm {b}} \ \),\( \ {\dot V}_{\mathrm {c}} \ \)は以下のように表せます。ただし,\( \ a \ \)はベクトルオペレータとなります。
\[
\begin{eqnarray}
{\dot V}_{\mathrm {a}} &=&{\dot V}_{0}+ {\dot V}_{1} + {\dot V}_{2} \\[ 5pt ]
{\dot V}_{\mathrm {b}} &=&{\dot V}_{0}+ a^{2}{\dot V}_{1} + a{\dot V}_{2} \\[ 5pt ]
{\dot V}_{\mathrm {c}} &=&{\dot V}_{0}+ a{\dot V}_{1} + a^{2}{\dot V}_{2} \\[ 5pt ]
\end{eqnarray}
\]
零相電流\( \ {\dot I}_{0} \ \),正相電流\( \ {\dot I}_{1} \ \),逆相電流\( \ {\dot I}_{2} \ \)とすると,各相の電流\( \ {\dot I}_{\mathrm {a}} \ \),\( \ {\dot I}_{\mathrm {b}} \ \),\( \ {\dot I}_{\mathrm {c}} \ \)は電圧同様に以下のように表せます。
\[
\begin{eqnarray}
{\dot I}_{\mathrm {a}} &=&{\dot I}_{0}+ {\dot I}_{1} + {\dot I}_{2} \\[ 5pt ]
{\dot I}_{\mathrm {b}} &=&{\dot I}_{0}+ a^{2}{\dot I}_{1} + a{\dot I}_{2} \\[ 5pt ]
{\dot I}_{\mathrm {c}} &=&{\dot I}_{0}+ a{\dot I}_{1} + a^{2}{\dot I}_{2} \\[ 5pt ]
\end{eqnarray}
\]
また,対称座標法における発電機の基本式は以下の通りとなります。
\[
\begin{eqnarray}
{\dot V}_{0} &=&-Z_{0}{\dot I}_{0} \\[ 5pt ]
{\dot V}_{1} &=&{\dot E}_{\mathrm {a}}-Z_{1}{\dot I}_{1} \\[ 5pt ]
{\dot V}_{2} &=&-Z_{2}{\dot I}_{2} \\[ 5pt ]
\end{eqnarray}
\]
これらの式を利用して,地絡電流の大きさを求めます。
3.対称座標法による\( \ 1 \ \)線地絡故障時の等価回路
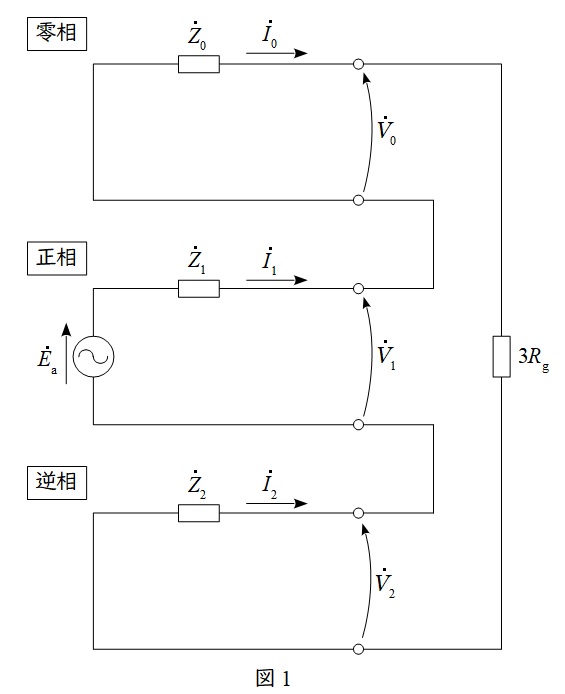
対称座標法を利用した\( \ 1 \ \)線地絡故障時の等価回路は図1のようになります。ただし,\( \ R_{\mathrm {g}} \ \)は地絡抵抗となります。発電機の基本式と照らし合わせて覚えましょう。
【関連する「電気の神髄」記事】
対称座標法変換の基本式
対称座標法における発電機の基本式
一線地絡時の故障計算(対称座標法)
一線地絡時の故障計算(零相インピーダンス以外を無視できる場合)
【解答】
(1)地絡電流\( \ {\dot I}_{\mathrm {g}} \ \)を各値を用いて表す
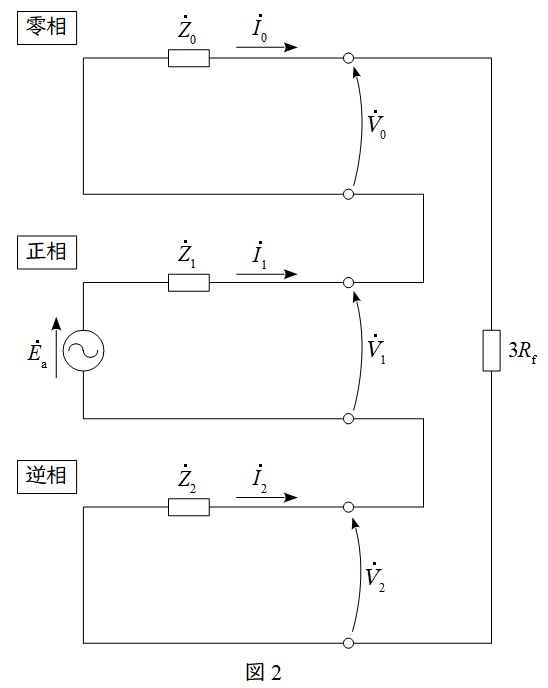
本問における\( \ 1 \ \)線地絡故障時の等価回路を図2に示す。
図2より,
\[
\begin{eqnarray}
{\dot I}_{0}&=&{\dot I}_{1}&=&{\dot I}_{2} \\[ 5pt ]
\end{eqnarray}
\]
であるから,回路方程式より\( \ {\dot I}_{\mathrm {0}} \ \)を求めると,
\[
\begin{eqnarray}
{\dot V}_{0}+ {\dot V}_{1} + {\dot V}_{2}&=&3R_{\mathrm {f}}{\dot I}_{0} \\[ 5pt ]
-Z_{0}{\dot I}_{0}+{\dot E}_{\mathrm {a}}-Z_{1}{\dot I}_{1}-Z_{2}{\dot I}_{2}&=&3R_{\mathrm {f}}{\dot I}_{0} \\[ 5pt ]
-Z_{0}{\dot I}_{0}+{\dot E}_{\mathrm {a}}-Z_{1}{\dot I}_{0}-Z_{2}{\dot I}_{0}&=&3R_{\mathrm {f}}{\dot I}_{0} \\[ 5pt ]
{\dot E}_{\mathrm {a}}-\left( Z_{0}+Z_{1}+Z_{2}\right) {\dot I}_{0}&=&3R_{\mathrm {f}}{\dot I}_{0} \\[ 5pt ]
\left( Z_{0}+Z_{1}+Z_{2}+3R_{\mathrm {f}}\right) {\dot I}_{0}&=&{\dot E}_{\mathrm {a}} \\[ 5pt ]
{\dot I}_{0}&=&\frac {{\dot E}_{\mathrm {a}}}{Z_{0}+Z_{1}+Z_{2}+3R_{\mathrm {f}}} \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,問題図より,\( \ {\dot I}_{\mathrm {g}}={\dot I}_{\mathrm {a}} \ \)であり,ワンポイント解説「2.対称座標法」より,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {a}} &=&{\dot I}_{0}+ {\dot I}_{1} + {\dot I}_{2} \\[ 5pt ]
&=&3{\dot I}_{0} \\[ 5pt ]
\end{eqnarray}
\]
であるから,地絡電流\( \ {\dot I}_{\mathrm {g}} \ \)は,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {g}} &=&3{\dot I}_{0} \\[ 5pt ]
&=&\frac {3{\dot E}_{\mathrm {a}}}{Z_{0}+Z_{1}+Z_{2}+3R_{\mathrm {f}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)零相インピーダンス\( \ {\dot Z}_{\mathrm {0}} \ \),正相インピーダンス\( \ {\dot Z}_{\mathrm {1}} \ \),逆相インピーダンス\( \ {\dot Z}_{\mathrm {2}} \ \)を求める
題意より,対地静電容量\( \ C \ \)と変圧器の中性点の抵抗\( \ R_{\mathrm {e}} \ \)以外は無視するものとするとなっているので,零相分以外のインピーダンスは無視できる。したがって,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {1}}&=&{\dot Z}_{\mathrm {2}}&=&0 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
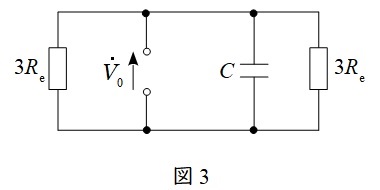
と求められる。また,零相回路における事故点から見た等価回路は図3のようになるので(※中性点抵抗が\( \ 3 \ \)倍になる等の等価回路の詳細は複雑になるので試験では覚えましょう。興味のある方は電気の神髄HPをご覧下さい。),
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {0}}&=&\frac {\displaystyle \frac {3}{2}R_{\mathrm {e}}\cdot \frac {1}{\mathrm {j}\omega C}}{\displaystyle \frac {3}{2}R_{\mathrm {e}}+\frac {1}{\mathrm {j}\omega C}} \\[ 5pt ]
&=&\frac {\displaystyle \frac {3}{2}R_{\mathrm {e}}\cdot \frac {1}{\mathrm {j}\omega C}}{\displaystyle \frac {\displaystyle 1+\frac {3}{2}\mathrm {j}\omega CR_{\mathrm {e}}}{\mathrm {j}\omega C}} \\[ 5pt ]
&=&\frac {3R_{\mathrm {e}}}{\displaystyle 2+3\mathrm {j}\omega CR_{\mathrm {e}}} \\[ 5pt ]
&=&\frac {3R_{\mathrm {e}}\left( 2-3\mathrm {j}\omega CR_{\mathrm {e}}\right) }{\displaystyle 4+9\left( \omega CR_{\mathrm {e}}\right) ^{2}} \\[ 5pt ]
&=&\frac {\displaystyle 3\times \frac {2000}{3}\times \left( 2-3\times \mathrm {j}2\times 3.1416 \times 50 \times 0.005\times 10^{-6}\times 20 \times \frac {2000}{3}\right) }{\displaystyle 4+9\times \left( 2\times 3.1416 \times 50 \times 0.005\times 10^{-6}\times 20 \times \frac {2000}{3}\right) ^{2}} \\[ 5pt ]
&≒&\frac {4000- \mathrm {j}125.66 }{\displaystyle 4+9\times 0.020944 ^{2}} \\[ 5pt ]
&≒&999.01-\mathrm {j}31.384 → 999-\mathrm {j}31.4 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)地絡電流の大きさ\( \ \left| {\dot I}_{\mathrm {g}}\right| \ \mathrm {[A]} \ \)を求める
(1)及び(2)より,(1)解答式を整理して各値を代入すると,
\[
\begin{eqnarray}
\left| {\dot I}_{\mathrm {g}} \right| &=&\left| \frac {3{\dot E}_{\mathrm {a}}}{Z_{0}+Z_{1}+Z_{2}+3R_{\mathrm {f}}}\right| \\[ 5pt ]
&=&\left| \frac {\displaystyle 3\times \frac {66000}{\sqrt {3}} }{999.01-\mathrm {j}31.384+0+0+3\times 10}\right| \\[ 5pt ]
&=&\left| \frac {66000\sqrt {3}}{1029.01-\mathrm {j}31.384}\right| \\[ 5pt ]
&=&\frac {66000\sqrt {3}}{\sqrt {1029.01^{2}+31.384^{2}}} \\[ 5pt ]
&≒&111 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは