【問題】
【難易度】★★★★☆(やや難しい)
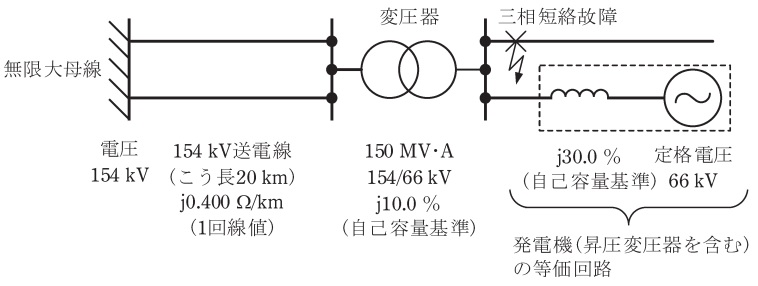
単位法を用いた三相回路の故障電流の検討について以下の問に答えよ。
(1) 線間電圧\( \ 154 \ \mathrm {kV} \ \),三相容量\( \ 100 \ \mathrm {MV\cdot A} \ \)を基準値とするとき,次を求めよ。
a) 基準電流\( \ I_{\mathrm {B}} \ \mathrm {[kA]} \ \)
b) 基準インピーダンス\( \ Z_{\mathrm {B}} \ \mathrm {[\Omega]} \ \)
(2) 図に示す無限大母線と送電線,変圧器,発電機から構成される電力系統を対象として,以下の量を,\( \ 100 \ \mathrm {MV\cdot A} \ \)を基準容量とし各部の公称電圧ないしは定格電圧を基準電圧とする単位法による値に換算せよ。
a) 公称電圧\( \ 154 \ \mathrm {kV} \ \)のこう長\( \ 20 \ \mathrm {km} \ \)の\( \ 1 \ \)回線送電線のインピーダンスを上記の単位法の値\( \ \mathrm {[p.u.]} \ \)に換算せよ。ただし,送電線(1回線)のインピーダンスは\( \ \mathrm {j}0.400 \ \mathrm {\Omega / km} \ \)とする。
b) 容量\( \ 150 \ \mathrm {MV\cdot A} \ \)の変圧器\( \ \left( 154 / 66 \ \mathrm {kV}\right) \ \)のインピーダンスを上記の単位法の値\( \ \mathrm {[p.u.]} \ \)に換算せよ。ただし,同変圧器のインピーダンスは自己容量基準で\( \ \mathrm {j}10.0 \ \mathrm {%} \ \)とする。
c) 変圧器二次側(定格電圧\( \ 66 \ \mathrm {kV} \ \))の電流\( \ 25 \ \mathrm {kA} \ \)を上記の単位法の値\( \ \mathrm {[p.u.]} \ \)に換算せよ。
(3) 図の電力系統で,変圧器二次側(定格電圧\( \ 66 \ \mathrm {kV} \ \))の母線至近端での三相短絡時における故障電流を\( \ 25 \ \mathrm {kA} \ \)以下に抑えることができる発電機の最大容量\( \ S \ \mathrm {[MV\cdot A]} \ \)を求めよ。ここに送電線と変圧器のインピーダンスは小問(2)に示すとおりであるが,\( \ 154 \ \mathrm {kV} \ \)送電線は\( \ 2 \ \)回線とする。また発電機(昇圧変圧器を含む)は,定格電圧が\( \ 66 \ \mathrm {kV} \ \)の電圧源と自己容量基準で\( \ \mathrm {j}30.0 \ \mathrm {%} \ \)のインピーダンスの直列回路で表すこととする。なお無限大母線の電圧は\( \ 154 \ \mathrm {kV} \ \),電圧源の電圧は\( \ 66 \ \mathrm {kV} \ \)とする。
【ワンポイント解説】
単位法を用いた三相回路の故障電流計算に関する問題です。
よくあるパターンの問題で(1)及び(2)は比較的易しい問題ですが,(3)がやや計算量の多い問題です。
合格するためには,このような問題は(2)までを確実に得点し,(3)は他の問題が終わり最後時間が余った場合にじっくりと解くと良いと思います。
1.オーム法から単位法への変換
基準容量を\( \ P_{\mathrm {n}} \ \mathrm {[V\cdot A]} \ \),基準電圧を\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \),基準電流を\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)とすると,
\[
\begin{eqnarray}
Z \ \mathrm {[p.u.]} \ &=&\frac {Z \ \mathrm {[\Omega ]} \ I_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}} (定義) \\[ 5pt ]
&=&\frac {\sqrt {3}Z \ \mathrm {[\Omega ]} \ I_{\mathrm {n}}}{V_{\mathrm {n}}} \\[ 5pt ]
&=&\frac {\sqrt {3}Z \ \mathrm {[\Omega ]} \ V_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}} \\[ 5pt ]
&=&\frac {P_{\mathrm {n}}Z \ \mathrm {[\Omega ]} \ }{V_{\mathrm {n}}^{2}} (∵P_{\mathrm {n}}=\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} ) \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.単位法における容量換算
「1.オーム法から単位法への変換」の通り,単位法における\( \ \mathrm {p.u.} \ \)値は基準容量に比例します。したがって,基準容量\( \ P_{\mathrm {A}} \ \mathrm {[V\cdot A]} \ \)から\( \ P_{\mathrm {B}} \ \mathrm {[V\cdot A]} \ \)へ容量換算する場合,
\[
\begin{eqnarray}
Z_{\mathrm {B}} \ \mathrm {[p.u.]} \ &=&\frac {P_{\mathrm {B}}}{P_{\mathrm {A}}}Z_{\mathrm {A}} \ \mathrm {[p.u.]} \ \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.単位法における三相短絡電流計算
単位法における故障点から電源側を見た線路のインピーダンスを\( \ Z_{\mathrm {s}} \ \mathrm {[p.u.]} \ \)とすると,三相短絡電流\( \ I_{\mathrm {s}} \ \mathrm {[A]} \ \)は,基準電流\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)を用いて,
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {I_{\mathrm {n}}}{Z_{\mathrm {s}} \ \mathrm {[p.u.]}} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
※単位法の定義式等を用いて\( \ \displaystyle I_{\mathrm {s}}=\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}} \ \)から上式を求めることはできますが,試験時には暗記しておいた方が良いと思います。
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}{Z_{\mathrm {s}} \ \mathrm {[\Omega ]}} \\[ 5pt ]
&=&\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}} \\[ 5pt ]
&=&\frac {V_{\mathrm {n}}I_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}I_{\mathrm {n}}} \\[ 5pt ]
&=&\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}I_{\mathrm {n}}}\times I_{\mathrm {n}} \\[ 5pt ]
&=&\frac {I_{\mathrm {n}}}{Z_{\mathrm {s}} \ \mathrm {[p.u.]}} \\[ 5pt ]
\end{eqnarray}
\]
【解答】
(1)a)基準電流\( \ I_{\mathrm {B}} \ \mathrm {[kA]} \ \)
線間電圧\( \ V_{\mathrm {B}}=154 \ \mathrm {[kV]} \ \),三相容量\( \ P_{\mathrm {B}}=100 \ \mathrm {[MV\cdot A]} \ \)を基準とするので,
\[
\begin{eqnarray}
P_{\mathrm {B}}&=&\sqrt {3}V_{\mathrm {B}}I_{\mathrm {B}} \\[ 5pt ]
I_{\mathrm {B}}&=&\frac {P_{\mathrm {B}}}{\sqrt {3}V_{\mathrm {B}}} \\[ 5pt ]
&=&\frac {100\times 10^{6}}{\sqrt {3}\times 154\times 10^{3}} \\[ 5pt ]
&≒&374.90 \ \mathrm {[A]} → 0.375 \ \mathrm {[kA]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(1)b)基準インピーダンス\( \ Z_{\mathrm {B}} \ \mathrm {[\Omega]} \ \)
線間電圧\( \ V_{\mathrm {B}}=154 \ \mathrm {[kV]} \ \),基準電流\( \ I_{\mathrm {B}}=374.90 \ \mathrm {[A]} \ \)であるから,
\[
\begin{eqnarray}
\frac {V_{\mathrm {B}}}{\sqrt {3}}&=&Z_{\mathrm {B}}I_{\mathrm {B}} \\[ 5pt ]
Z_{\mathrm {B}}&=&\frac {V_{\mathrm {B}}}{\sqrt {3}I_{\mathrm {B}}} \\[ 5pt ]
&=&\frac {154\times 10^{3}}{\sqrt {3}\times 374.90} \\[ 5pt ]
&≒&237.16 → 237 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)a)公称電圧\( \ 154 \ \mathrm {kV} \ \)のこう長\( \ 20 \ \mathrm {km} \ \)の\( \ 1 \ \)回線送電線のインピーダンスを単位法\( \ \mathrm {[p.u.]} \ \)に換算
\( \ 154 \ \mathrm {kV} \ \)の送電線のインピーダンス\( \ Z_{\mathrm {1}} \ \mathrm {[\Omega ]} \ \)は,送電線(1回線)の\( \ 1 \ \mathrm {km} \ \)当たりのインピーダンスが\( \ z_{\mathrm {1}}=\mathrm {j}0.400 \ \mathrm {[\Omega / km]} \ \),送電線のこう長が\( \ l_{\mathrm {1}}=20 \ \mathrm {[km]} \ \)であるから,
\[
\begin{eqnarray}
Z_{\mathrm {1}}&=&z_{\mathrm {1}} l_{\mathrm {1}} \\[ 5pt ]
&=&\mathrm {j}0.400\times 20 \\[ 5pt ]
&≒&\mathrm {j}8.00 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,ワンポイント解説「1.オーム法から単位法への変換」の通り,単位法におけるインピーダンス\( \ Z_{\mathrm {1}} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
Z_{\mathrm {1}} \ \mathrm {[p.u.]} \ &=&\frac {\sqrt {3}Z_{\mathrm {1}} \ \mathrm {[\Omega ]} \ I_{\mathrm {B}}}{V_{\mathrm {B}}} \\[ 5pt ]
&=&\frac {\sqrt {3}\times \mathrm {j}8.00 \times 374.90}{154\times 10^{3}} \\[ 5pt ]
&≒&\mathrm {j}0.033732 → \mathrm {j}0.0337 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)b)容量\( \ 150 \ \mathrm {kV\cdot A} \ \)の変圧器のインピーダンスを単位法\( \ \mathrm {[p.u.]} \ \)に換算
ワンポイント解説「2.単位法における容量換算」の通り,基準容量\( \ P_{\mathrm {B}}=100 \ \mathrm {[MV\cdot A]} \ \)におけるインピーダンス\( \ Z_{\mathrm {T}} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
Z_{\mathrm {T}} \ \mathrm {[p.u.]} \ &=&\frac {100\times 10^{6}}{150\times 10^{6}}\times \mathrm {j}0.1 \ \\[ 5pt ]
&≒&\mathrm {j}0.066667 → \mathrm {j}0.0667 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)c)変圧器二次側(定格電圧\( \ 66 \ \mathrm {kV} \ \))の電流\( \ 25 \ \mathrm {kA} \ \)を単位法\( \ \mathrm {[p.u.]} \ \)に換算
変圧器二次側の基準電流\( \ I_{\mathrm {B}}^{\prime } \ \mathrm {[kA]} \ \)は,線間電圧\( \ V_{\mathrm {B}}^{\prime }=66 \ \mathrm {[kV]} \ \),三相容量\( \ P_{\mathrm {B}}=100 \ \mathrm {[MV\cdot A]} \ \)を基準とするので,
\[
\begin{eqnarray}
P_{\mathrm {B}}&=&\sqrt {3}V_{\mathrm {B}}^{\prime }I_{\mathrm {B}}^{\prime } \\[ 5pt ]
I_{\mathrm {B}}^{\prime }&=&\frac {P_{\mathrm {B}}}{\sqrt {3}V_{\mathrm {B}}^{\prime }} \\[ 5pt ]
&=&\frac {100\times 10^{6}}{\sqrt {3}\times 66\times 10^{3}} \\[ 5pt ]
&≒&874.77 \ \mathrm {[A]} → 0.87477 \ \mathrm {[kA]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,電流\( \ I_{\mathrm {2}}=25 \ \mathrm {[kA]} \ \)の単位法における電流値\( \ I_{\mathrm {2}} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {2}} \ \mathrm {[p.u.]} \ &=&\frac {I_{\mathrm {2}} \ \mathrm {[kA]} }{I_{\mathrm {B}}^{\prime }} \\[ 5pt ]
&=&\frac {25}{0.87477} \\[ 5pt ]
&≒&28.579 → 28.6 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
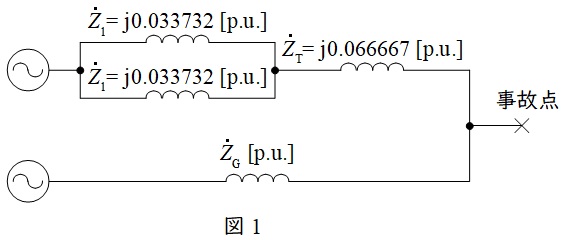
(3)変圧器二次側(定格電圧\( \ 66 \ \mathrm {kV} \ \))の母線至近端での三相短絡時における故障電流を\( \ 25 \ \mathrm {kA} \ \)以下に抑えることができる発電機の最大容量\( \ S \ \mathrm {[MV\cdot A]} \ \)
事故点から電源側を見た等価回路は図1の通りとなる。
ワンポイント解説「3.単位法における三相短絡電流計算」の通り,故障電流が\( \ I_{\mathrm {2}}=25 \ \mathrm {[kA]} \ \)の時の事故点から見たインピーダンス\( \ Z_{\mathrm {s}} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {2}}&=&\frac {I_{\mathrm {B}}^{\prime }}{Z_{\mathrm {s}} \ \mathrm {[p.u.]}} \\[ 5pt ]
Z_{\mathrm {s}} \ \mathrm {[p.u.]}&=&\frac {I_{\mathrm {B}}^{\prime }}{I_{\mathrm {2}}} \\[ 5pt ]
&=&\frac {874.77}{25\times 10^{3}} \\[ 5pt ]
&≒&0.034991 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となり,図1の合成インピーダンスが上記値以上となれば良いので,
\[
\begin{eqnarray}
Z_{\mathrm {s}}&≦&\frac {\displaystyle \left( \frac {Z_{\mathrm {1}}}{2}+Z_{\mathrm {T}}\right) Z_{\mathrm {G}}}{\displaystyle \left( \frac {Z_{\mathrm {1}}}{2}+Z_{\mathrm {T}}\right) +Z_{\mathrm {G}} } \\[ 5pt ]
Z_{\mathrm {s}}\left\{ \left( \frac {Z_{\mathrm {1}}}{2}+Z_{\mathrm {T}}\right) +Z_{\mathrm {G}} \right\} &≦&\left( \frac {Z_{\mathrm {1}}}{2}+Z_{\mathrm {T}}\right) Z_{\mathrm {G}} \\[ 5pt ]
Z_{\mathrm {s}}\left( \frac {Z_{\mathrm {1}}}{2}+Z_{\mathrm {T}}\right) +Z_{\mathrm {s}}Z_{\mathrm {G}} &≦&\left( \frac {Z_{\mathrm {1}}}{2}+Z_{\mathrm {T}}\right) Z_{\mathrm {G}} \\[ 5pt ]
\left( \frac {Z_{\mathrm {1}}}{2}+Z_{\mathrm {T}}-Z_{\mathrm {s}}\right) Z_{\mathrm {G}} &≧&Z_{\mathrm {s}}\left( \frac {Z_{\mathrm {1}}}{2}+Z_{\mathrm {T}}\right) \\[ 5pt ]
Z_{\mathrm {G}} &≧&\frac {\displaystyle Z_{\mathrm {s}}\left( \frac {Z_{\mathrm {1}}}{2}+Z_{\mathrm {T}}\right) }{\displaystyle \frac {Z_{\mathrm {1}}}{2}+Z_{\mathrm {T}}-Z_{\mathrm {s}}} \\[ 5pt ]
&=&\frac {\displaystyle \mathrm {j}0.034991 \times \left( \frac {\mathrm {j}0.033732}{2}+\mathrm {j}0.066667 \right) }{\displaystyle \frac {\mathrm {j}0.033732}{2}+\mathrm {j}0.066667-\mathrm {j}0.034991} \\[ 5pt ]
&≒&\frac {-0.0029229}{\mathrm {j}0.048542} \\[ 5pt ]
&≒&\mathrm {j}0.060214 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となる。発電機の容量を\( \ S \ \mathrm {[MV\cdot A]} \ \)としたときの単位法におけるインピーダンスが\( \ Z_{\mathrm {G}}^{\prime }=\mathrm {j}0.3 \ \mathrm {[p.u.]} \ \)なので,ワンポイント解説「2.単位法における容量換算」の通り,
\[
\begin{eqnarray}
Z_{\mathrm {G}} &=&\frac {100}{S}Z_{\mathrm {G}}^{\prime } \\[ 5pt ]
S &=&\frac {100}{Z_{\mathrm {G}}}Z_{\mathrm {G}}^{\prime } \\[ 5pt ]
&=&\frac {100}{\mathrm {j}0.060214}\times \mathrm {j}0.3 \\[ 5pt ]
&≒&498 \ \mathrm {[MV\cdot A]} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,発電機の最大容量\( \ S \ \mathrm {[MV\cdot A]} \ \)は\( \ 498 \ \mathrm {MV\cdot A} \ \)と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは