《電力・管理》〈配電〉[R05:問4]分散型電源設置前後の電圧の導出に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

配電系統の電圧に関して，次の問に答えよ。

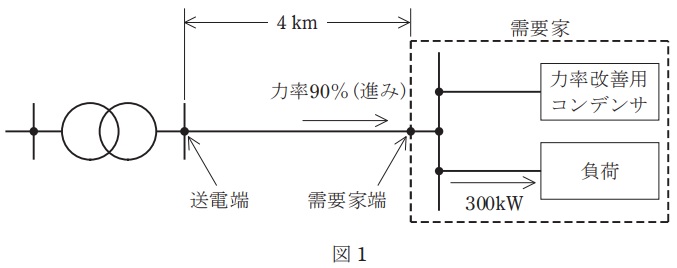
図1のように，こう長\( \ 4 \ \mathrm {km} \ \)の三相高圧配電線の末端に\( \ 300 \ \mathrm {kW} \ \)の三相負荷，力率改善後の力率（進み）\( \ 90 \ \mathrm {％} \ \)の需要家が接続されている。

(1)　需要家端の線間電圧を\( \ 6 \ 600 \ \mathrm {V} \ \)とするとき，送電端電圧を求めよ。

　なお，\( \ 1 \ \)相当たりの線路抵抗及びリアクタンスを，それぞれ\( \ 0.2 \ \mathrm {\Omega / km} \ \)，\( \ 0.6 \ \mathrm {\Omega / km} \ \)とする。

　また，電圧計算の近似式を用いること。

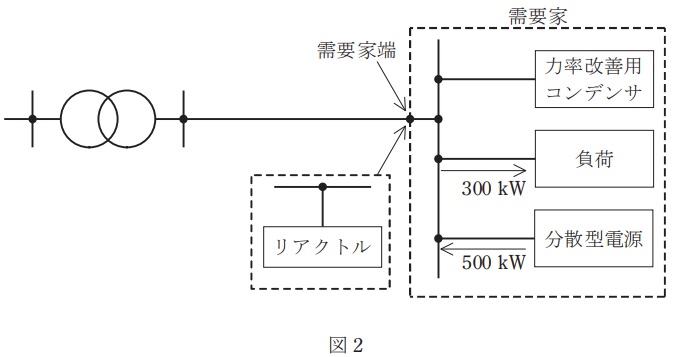
(2)　小問(1)の系統において，図2のように，需要家の構内に新たに分散型電源を設置した。送電端の線間電圧が\( \ 6 \ 600 \ \mathrm {V} \ \)である場合，送電端と需要家端の電圧を同じ電圧\( \ \left( 6 \ 600 \ \mathrm {V}\right) \ \)に保つために需要家端に設置が必要なリアクトル容量\( \ Q_{1} \ \mathrm {[kvar]} \ \)を求めよ。分散型電源の出力は\( \ 500 \ \mathrm {kW} \ \)，力率は\( \ 100 \ \mathrm {％} \ \)とする。

　なお，電圧計算の近似式を用いること。

【ワンポイント解説】

分散型電源設置前後の電圧及びリアクトル容量を求める問題です。
電験\( \ 2 \ \)種受験生ならば電圧降下の近似式は知っている方がほとんどであると思いますが，本問は進み力率であること等が受験生を惑わせている問題です。
遅れ無効電力を正として，プラスマイナスを間違えないように注意しましょう。

1.送配電線の電圧降下
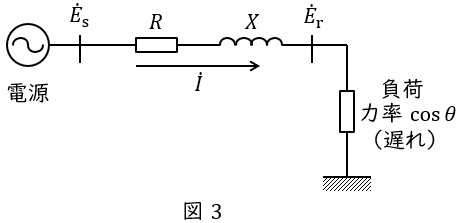
図3のような一般的な三相\( \ 3 \ \)線式送配電線路において，送配電線には抵抗\( \ R \ \mathrm {[\Omega ]} \ \)及びリアクタンス\( \ X \ \mathrm {[\Omega ]} \ \)があるため，送配電線での抵抗降下やリアクタンス降下が発生します。
送電端電圧（相電圧）を\( \ {\dot E}_{\mathrm {s}} \ \mathrm {[V]} \ \)，受電端に力率\( \ \cos \theta \ \)の負荷を接続したときの受電端電圧（相電圧）を\( \ {\dot E}_{\mathrm {r}} \ \mathrm {[V]} \ \)，送配電線に流れる電流を\( \ \dot I \ \mathrm {[A]} \ \)とすると，
\[
\begin{eqnarray}
{\dot E}_{\mathrm {s}} &=&{\dot E}_{\mathrm {r}}+\left( R+\mathrm {j}X \right) \dot I \\[ 5pt ] \end{eqnarray}
\] の関係があるため，ベクトル図で表すと図4のようになります。

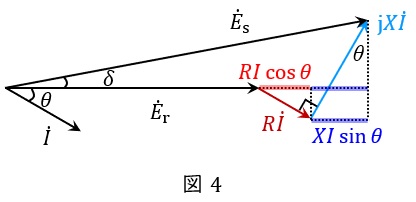
\( \ {\dot E}_{\mathrm {s}} \ \)と\( \ {\dot E}_{\mathrm {r}} \ \)の位相差が十分に小さいと仮定すると，線路の電圧降下\( \ \varepsilon =\sqrt {3}E_{\mathrm {s}}-\sqrt {3}E_{\mathrm {r}} \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
E_{\mathrm {s}}&≃&E_{\mathrm {r}}+RI\cos \theta +XI\sin \theta \\[ 5pt ] E_{\mathrm {s}}-E_{\mathrm {r}}&=&RI\cos \theta +XI\sin \theta \\[ 5pt ] \sqrt {3}E_{\mathrm {s}}-\sqrt {3}E_{\mathrm {r}}&=&\sqrt {3}\left( RI\cos \theta +XI\sin \theta \right) \\[ 5pt ] \varepsilon &=&\sqrt {3}I\left( R\cos \theta +X\sin \theta \right) \\[ 5pt ] \end{eqnarray}
\] で求められます。

2.三相\( \ 3 \ \)線式線路の有効電力\( \ P \ \)
三相\( \ 3 \ \)線式の送配電線の線間電圧が\( \ V \ \mathrm {[V]} \ \)，線電流が\( \ I \ \mathrm {[A]} \ \)，電圧と電流の力率が\( \ \cos \theta \ \)であるとき，送電電力\( \ P \ \mathrm {[W]} \ \)は，
\[
\begin{eqnarray}
P &=&\sqrt {3}VI\cos \theta \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)需要家端の線間電圧を\( \ 6 \ 600 \ \mathrm {V} \ \)とするときの送電端電圧
有効電力を求める式より，配電線を流れる電流\( \ I \ \mathrm {[A]} \ \)は，ワンポイント解説「2.三相\( \ 3 \ \)線式線路の有効電力\( \ P \ \)」の通り，
\[
\begin{eqnarray}
I &=&\frac {P}{\sqrt {3}V_{\mathrm {r}}\cos \theta } \\[ 5pt ] &=&\frac {300\times 10^{3}}{\sqrt {3}\times 6 \ 600 \times 0.9} \\[ 5pt ] &≒&29.159 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] であり，線路\( \ 1 \ \)相当たりの線路抵抗\( \ R \ \mathrm {[\Omega ]} \ \)及びリアクタンス\( \ X \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
R &=&0.2\times 4 \\[ 5pt ] &=&0.8 \ \mathrm {[\Omega ]} \\[ 5pt ] X &=&0.6\times 4 \\[ 5pt ] &=&2.4 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] である。また，負荷の\( \ \sin \theta \ \)は，進み力率であることに注意すると，
\[
\begin{eqnarray}
\sin \theta &=&-\sqrt {1-\cos ^{2}\theta }\\[ 5pt ] &=&-\sqrt {1-0.9^{2}} \\[ 5pt ] &≒&-0.43589 \\[ 5pt ] \end{eqnarray}
\] であるから，配電線での電圧降下\( \ \varepsilon \ \mathrm {[V]} \ \)は，ワンポイント解説「1.送配電線の電圧降下」の通り，
\[
\begin{eqnarray}
\varepsilon &=&\sqrt {3}I\left( R\cos \theta +X\sin \theta \right) \\[ 5pt ] &=&\sqrt {3}\times 29.159 \times \left\{ 0.8 \times 0.9 +2.4\times \left( -0.43589\right) \right\} \\[ 5pt ] &≒&-16.471 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となるので，送電端電圧\( \ V_{\mathrm {s}} \ \mathrm {[V]} \ \)は，需要家端電圧\( \ V_{\mathrm {r}}=6 \ 600 \ \mathrm {[V]} \ \)であるから，
\[
\begin{eqnarray}
V_{\mathrm {s}} &=&V_{\mathrm {r}}+\varepsilon \\[ 5pt ] &=&6 \ 600-16.471 \\[ 5pt ] &≒&6 \ 583.5　→　6 \ 580 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)分散型電源設置後，送電端と需要家端の電圧を同じ電圧\( \ \left( 6 \ 600 \ \mathrm {V}\right) \ \)に保つために需要家端に設置が必要なリアクトル容量\( \ Q_{1} \ \mathrm {[kvar]} \ \)
分散型電源及びリアクトル設置前の需要家端の無効電力\( \ Q \ \mathrm {[kvar]} \ \)は，遅れ無効電力を正とすると，
\[
\begin{eqnarray}
Q &=&P \tan \theta \\[ 5pt ] &=&P \frac {\sin \theta }{\cos \theta } \\[ 5pt ] &=&300\times \frac {-0.43589}{0.9} \\[ 5pt ] &≒&-145.30 \ \mathrm {[kvar]} \\[ 5pt ] \end{eqnarray}
\] であり，需要家端にリアクトルを設置した後の力率を\( \ \cos \theta ^{\prime } \ \)とすると，このときの線路の電圧降下\( \ \varepsilon ^{\prime } \ \)が零であるから，
\[
\begin{eqnarray}
\varepsilon ^{\prime } &=&\sqrt {3}I\left( R\cos \theta ^{\prime } +X\sin \theta ^{\prime } \right) \\[ 5pt ] 0 &=&\sqrt {3}I\left( R\cos \theta ^{\prime } +X\sin \theta ^{\prime } \right) \\[ 5pt ] 0 &=& R\cos \theta ^{\prime } +X\sin \theta ^{\prime } \\[ 5pt ] 0 &=& 0.8\cos \theta ^{\prime } +2.4\sin \theta ^{\prime } \\[ 5pt ] 2.4\sin \theta ^{\prime } &=& -0.8\cos \theta ^{\prime } \\[ 5pt ] \frac {\sin \theta ^{\prime }}{\cos \theta ^{\prime }}&=& -\frac {0.8}{2.4} \\[ 5pt ] \tan \theta ^{\prime }&≒& -0.33333 \\[ 5pt ] \end{eqnarray}
\] となる。よって，このときの需要家端の無効電力\( \ Q^{\prime } \ \mathrm {[kvar]} \ \)は，
\[
\begin{eqnarray}
Q^{\prime } &=&P^{\prime } \tan \theta ^{\prime } \\[ 5pt ] &=&\left( 300-500\right) \times \left( -0.33333\right) \\[ 5pt ] &≒&66.666 \ \mathrm {[kvar]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，必要なリアクトル容量\( \ Q_{\mathrm {1}} \ \mathrm {[kvar]} \ \)は，
\[
\begin{eqnarray}
Q_{\mathrm {1}} &=&Q^{\prime }-Q \\[ 5pt ] &=&66.666-\left( -145.30\right) \\[ 5pt ] &≒&212 \ \mathrm {[kvar]} \\[ 5pt ] \end{eqnarray}
\] と求められる。