Contents
【問題】
【難易度】★★★★☆（やや難しい）
図の制御系において，\( \ R(s) \ \)，\( \ E(s) \ \)，\( \ U(s) \ \)及び\( \ Y(s) \ \)は，目標値\( \ r(t) \ \)，偏差\( \ e(t) \ \)，操作量\( \ u(t) \ \)及び出力\( \ y(t) \ \)をそれぞれラプラス変換したものである。以下では，\( \ K_{1}＞0 \ \)，\( \ K_{2}＞0 \ \)とする。次の問に答えよ。
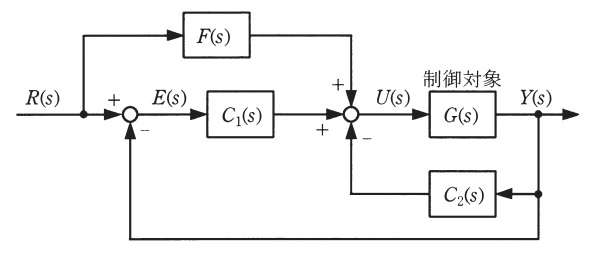
(1) 図の制御対象の伝達関数が\( \ \displaystyle G(s)=\frac {1}{s^{2}+4} \ \)で与えられるとき，制御対象の単位インパルス応答を求めよ。
(2) 上記(1)において，さらに\( \ F(s)=0 \ \)，\( \ \displaystyle C_{1}(s)=K_{1}\left( 1+\frac {1}{s}\right) \ \)，\( \ C_{2}(s)=K_{2}s \ \)のとき，\( \ R(s) \ \)から\( \ E(s) \ \)までの伝達関数を\( \ K_{1} \ \)と\( \ K_{2} \ \)を用いて表せ。
(3) 上記(2)において，図の制御系が安定限界となるとき，\( \ K_{1} \ \)と\( \ K_{2} \ \)が満たすべき関係を求めよ。またこのとき制御系が示す応答について簡単に述べよ。
(4) 次に，\( \ F(s)≠0 \ \)の場合を考える。次の空欄(a)～(f)に入る数式を\( \ F(s) \ \)，\( \ C_{1}(s) \ \)，\( \ C_{2}(s) \ \)，\( \ G(s) \ \)を用いてできるだけ簡略化して表せ。
図から
\[
\begin{eqnarray}
U(s)&=&\fbox { （a） } \cdot R(s) +\fbox { （b） } \cdot E(s) -\fbox { （c） } \cdot U(s) \\[ 5pt ]
E(s)&=&R(s) -\fbox { （d） } \cdot U(s) \\[ 5pt ]
\end{eqnarray}
\]
が成り立つ。これらから，\( \ R(s) \ \)から\( \ E(s) \ \)までの伝達関数を求めると
\[
\begin{eqnarray}
\frac {E(s)}{R(s)}&=&\frac {1+\fbox { （e） }}{1+\fbox { （f） }} \\[ 5pt ]
\end{eqnarray}
\]
となる。
(5) 上記(4)において，\( \ F(s)=4 \ \)，\( \ \displaystyle C_{1}(s)=K_{1}\left( 1+\frac {1}{s}\right) \ \)，\( \ C_{2}(s)=K_{2}s \ \)，\( \ \displaystyle G(s)=\frac {1}{s^{2}+4} \ \)を代入したとき，ランプ状の目標値\( \ r(t)=t \ \)に対する定常偏差を求めよ。
【ワンポイント解説】
自動制御を得意とする受験生は比較的多いですが，この年の問題は計算量が多く，解くのに時間がかかる問題となっています。練習でも時間を計測し，30分でどこまでできるかやってみるようにすると良いと思います。今回の伝達関数は分母が三次式となるので，ナイキストかラウスの安定判別法を用いる必要があります。
1.ナイキストの安定判別法
開ループ周波数伝達関数\(G_{0}( \mathrm {j}\omega )\)が与えられている時，\(G_{0}( \mathrm {j}\omega )\)が実軸と交わる点が，\( (-1，0 )\)より右側ならば安定，左側ならば不安定，\( (-1，0 )\)であれば安定限界となります。
2.ラウスの安定判別法
特性方程式\(a_{0}s^{n}+a_{1}s^{n-1}+a_{2}s^{n-2}+\cdots +a_{n-1}s+a_{n}=0\)が与えられている時，ラウスの安定判別法による安定条件は，
\[
\begin{eqnarray}
&&1. s^{3}，s^{2}，s^{1}，s^{0}の係数がすべて存在 \\[ 5pt ]
&&2. s^{3}，s^{2}，s^{1}，s^{0}の係数がすべて同符号 \\[ 5pt ]
&&3. ラウスの数表の値がすべて正であること \\[ 5pt ]
\end{eqnarray}
\]
です。ラウスの数表は下記図のようになります。
\[
\begin{array}{c|ccc}
& 1列 & 2列 & 3列 \\
\hline
1行 & a_{0} & a_{2} & a_{4} & \cdots \\
2行 & a_{1} & a_{3} & a_{5} & \cdots \\
3行 & b_{1}=\frac {a_{1}a_{2}-a_{0}a_{3}}{a_{1}} & b_{2}=\frac {a_{1}a_{4}-a_{0}a_{5}}{a_{1}} & \cdots \\
4行 & c_{1}=\frac {b_{1}a_{3}-a_{1}b_{2}}{b_{1}} & c_{2}=\frac {b_{1}a_{5}-a_{1}b_{3}}{b_{1}} & \cdots \\
\vdots & \vdots & \vdots &
\end{array}
\]
3.定常偏差(最終値の定理)
\( \ f(t) \ \)のラプラス変換を\( \ F(s) \ \)とすると，\( \ f(t) \ \)の定常偏差は，
\[
\begin{eqnarray}
\displaystyle \lim _{ t \to \infty } f(t)&=&\displaystyle \lim _{ s \to 0 } sF(s) \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
【解答】
(1)伝達関数が\( \ \displaystyle G(s)=\frac {1}{s^{2}+4} \ \)で与えられるとき，制御対象の単位インパルス応答
単位インパルス信号\( \ \delta (t) \)のラプラス変換は\( \ 1 \ \)であるから，
\[
\begin{eqnarray}
Y(s)&=&G(s)\cdot 1 \\[ 5pt ]
&=&\frac {1}{s^{2}+4} \\[ 5pt ]
\end{eqnarray}
\]
となる。\( \mathcal{L}[ \sin \omega t ] =\displaystyle \frac {\omega }{s^{2}+\omega ^{2}} \ \)の公式を利用して，ラプラス逆変換すると，
\[
\begin{eqnarray}
\mathcal{L}^{-1}[ Y(s) ] &=&\mathcal{L}^{-1}\left[ \frac {1}{s^{2}+4} \right] \\[ 5pt ]
&=&\mathcal{L}^{-1}\left[ \frac {1}{2}\cdot \frac {2}{s^{2}+2^{2}} \right] \\[ 5pt ]
&=&\frac {1}{2}\sin 2t \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)\( \ F(s)=0 \ \)，\( \ \displaystyle C_{1}(s)=K_{1}\left( 1+\frac {1}{s}\right) \ \)，\( \ C_{2}(s)=K_{2}s \ \)のとき，\( \ R(s) \ \)から\( \ E(s) \ \)までの伝達関数
問題図より，各関係式は，
\[
\begin{eqnarray}
R(s) -Y(s)&=&E(s) & ・・・・・・・・・ ①& \\[ 5pt ]
F(s)R(s)+C_{1}(s)E(s)-C_{2}(s)Y(s)&=&U(s) & ・・・・・・・・・ ②& \\[ 5pt ]
G(s)U(s)&=&Y(s) & ・・・・・・・・・ ③& \\[ 5pt ]
\end{eqnarray}
\]
で与えられる。③を①及び②に代入すると，
\[
\begin{eqnarray}
R(s) -G(s)U(s)&=&E(s) & ・・・ ①^{\prime }& \\[ 5pt ]
F(s)R(s)+C_{1}(s)E(s)-C_{2}(s)G(s)U(s)&=&U(s) && \\[ 5pt ]
F(s)R(s)+C_{1}(s)E(s)&=&\left( 1+C_{2}(s)G(s)\right) U(s) && \\[ 5pt ]
U(s)&=&\frac {F(s)R(s)+C_{1}(s)E(s)}{ 1+C_{2}(s)G(s)} & ・・・ ②^{\prime }& \\[ 5pt ]
\end{eqnarray}
\]
となり，\( \ F(s)=0 \ \)を\( \ ②^{\prime } \ \)に代入して，\( \ ②^{\prime } \ \)を\( \ ①^{\prime } \ \)に代入すると，
\[
\begin{eqnarray}
R(s) -G(s)\frac {C_{1}(s)E(s)}{ 1+C_{2}(s)G(s)}&=&E(s) \\[ 5pt ]
R(s)&=& \left( 1+\frac {C_{1}(s)G(s)}{ 1+C_{2}(s)G(s)}\right) E(s) \\[ 5pt ]
\frac {E(s)}{R(s)}&=&\frac { 1+C_{2}(s)G(s)}{1+C_{1}(s)G(s)+C_{2}(s)G(s)} \\[ 5pt ]
\end{eqnarray}
\]
となるので，各値を代入すると，
\[
\begin{eqnarray}
\frac {E(s)}{R(s)}&=&\frac { \displaystyle 1+K_{2}s\cdot \frac {1}{s^{2}+4}}{\displaystyle 1+K_{1}\left( 1+\frac {1}{s}\right) \frac {1}{s^{2}+4}+K_{2}s\cdot \frac {1}{s^{2}+4}} \\[ 5pt ]
&=&\frac { \displaystyle s\left( s^{2}+4\right) +K_{2}s^{2}}{\displaystyle s\left( s^{2}+4\right) +K_{1}\left( s+1\right) +K_{2}s^{2}} \\[ 5pt ]
&=&\frac { \displaystyle s\left( s^{2}+K_{2}s+4\right)}{\displaystyle s^{3}+K_{2}s^{2}+\left( K_{1}+4\right) s+K_{1}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)図の制御系が安定限界となるとき，\( \ K_{1} \ \)と\( \ K_{2} \ \)が満たすべき関係及びこのとき制御系が示す応答
ワンポイント解説「2.ラウスの安定判別法」より，ラウス表を作成すると，下表のようになる。
\[
\begin{array}{c|cc}
& 1列 & 2列 \\
\hline
1行 & 1 & K_{1}+4 \\
2行 & K_{2} & K_{1} \\
3行 & \frac {K_{2}\left( K_{1}+4\right) -K_{1}}{K_{2}} & 0 \\
4行 & K_{1} & \\
\end{array}
\]
上表より，安定限界の条件は，
\[
\begin{eqnarray}
\frac {K_{2}\left( K_{1}+4\right) -K_{1}}{K_{2}}&=&0 \\[ 5pt ]
K_{2}\left( K_{1}+4\right) -K_{1}&=&0 \\[ 5pt ]
K_{2}\left( K_{1}+4\right) &=&K_{1} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
安定限界のとき，制御系の応答は持続的な振動となる。
(4)空欄(a)～(f)に入る数式を\( \ F(s) \ \)，\( \ C_{1}(s) \ \)，\( \ C_{2}(s) \ \)，\( \ G(s) \ \)を用いて表す
③を①及び②に代入すると，
\[
\begin{eqnarray}
R(s) -G(s)U(s)&=&E(s) & ・・・ ①^{\prime \prime }& \\[ 5pt ]
F(s)R(s)+C_{1}(s)E(s)-C_{2}(s)G(s)U(s)&=&U(s) & ・・・ ②^{\prime \prime }& \\[ 5pt ]
\end{eqnarray}
\]
となり，(a)～(d)は求められる。また，\(②^{\prime \prime }\)を\( \ U(s) \ \)について整理すると，
\[
\begin{eqnarray}
F(s)R(s)+C_{1}(s)E(s)&=&\left( 1+C_{2}(s)G(s)\right) U(s) \\[ 5pt ]
U(s)&=&\frac {F(s)R(s)+C_{1}(s)E(s)}{1+C_{2}(s)G(s)} \\[ 5pt ]
\end{eqnarray}
\]
となり，これを\(①^{\prime \prime }\)に代入すると，
\[
\begin{eqnarray}
R(s) -G(s)\cdot \frac {F(s)R(s)+C_{1}(s)E(s)}{1+C_{2}(s)G(s)}&=&E(s) \\[ 5pt ]
\left[ 1+C_{2}(s)G(s)\right] R(s) -F(s)G(s)R(s)-C_{1}(s)G(s)E(s)&=&\left[ 1+C_{2}(s)G(s)\right] E(s) \\[ 5pt ]
\left[ 1+C_{2}(s)G(s)-F(s)G(s)\right] R(s) &=&\left[ 1+C_{1}(s)G(s)+C_{2}(s)G(s)\right] E(s) \\[ 5pt ]
\frac {E(s)}{R(s)} &=&\frac {1+C_{2}(s)G(s)-F(s)G(s)}{1+C_{1}(s)G(s)+C_{2}(s)G(s)} \\[ 5pt ]
\end{eqnarray}
\]
となり，(e)，(f)が求められる。
(5)\( \ F(s)=4 \ \)，\( \ \displaystyle C_{1}(s)=K_{1}\left( 1+\frac {1}{s}\right) \ \)，\( \ C_{2}(s)=K_{2}s \ \)，\( \ \displaystyle G(s)=\frac {1}{s^{2}+4} \ \)を代入したとき，ランプ状の目標値\( \ r(t)=t \ \)に対する定常偏差
(4)の解答式に各値を代入すると，
\[
\begin{eqnarray}
\frac {E(s)}{R(s)} &=&\frac {\displaystyle 1+K_{2}s\cdot \frac {1}{s^{2}+4}-4\cdot \frac {1}{s^{2}+4}}{\displaystyle 1+K_{1}\left( 1+\frac {1}{s}\right) \cdot \frac {1}{s^{2}+4}+K_{2}s\cdot \frac {1}{s^{2}+4}} \\[ 5pt ]
&=&\frac { \displaystyle s\left( s^{2}+4\right) +K_{2}s^{2}-4s}{\displaystyle s\left( s^{2}+4\right) +K_{1}\left( s+1\right) +K_{2}s^{2}} \\[ 5pt ]
&=&\frac { \displaystyle s^{2}\left( s+K_{2}\right)}{\displaystyle s^{3}+K_{2}s^{2}+\left( K_{1}+4\right) s+K_{1}} \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで，\( \ r(t)=t \ \)をラプラス変換すると\(\displaystyle \ R(s)=\frac {1}{s^{2}} \ \)であるから，これを代入すると，
\[
\begin{eqnarray}
E(s) &=&\frac { \displaystyle s^{2}\left( s+K_{2}\right)}{\displaystyle s^{3}+K_{2}s^{2}+\left( K_{1}+4\right) s+K_{1}}\cdot \frac {1}{s^{2}} \\[ 5pt ]
&=&\frac { \displaystyle s+K_{2}}{\displaystyle s^{3}+K_{2}s^{2}+\left( K_{1}+4\right) s+K_{1}} \\[ 5pt ]
\end{eqnarray}
\]
となる。ワンポイント解説「3.定常偏差(最終値の定理)」の通り，\( \ \displaystyle \lim _{ t \to \infty } f(t)=\displaystyle \lim _{ s \to 0 } sF(s) \ \)であるから，
\[
\begin{eqnarray}
\displaystyle \lim _{ s \to 0 } sE(s) &=&\displaystyle \lim _{ s \to 0 } \left[ s\cdot \frac { \displaystyle s+K_{2}}{\displaystyle s^{3}+K_{2}s^{2}+\left( K_{1}+4\right) s+K_{1}} \right] \\[ 5pt ]
&=&0 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
愛知県出身 愛称たけちゃん
詳しくは