【問題】
【難易度】★★☆☆☆(やや易しい)
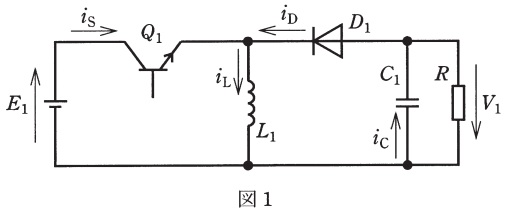
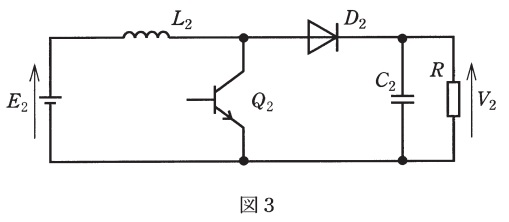
図1に示す昇降圧チョッパ及び図3に示す昇圧チョッパは,運転が定常状態にあるものとする。この動作特性について,次の問に答えよ。ただし,両図において,リアクトルのインダクタンスはその電流が連続するほどに適度に大きく,また,コンデンサの静電容量は出力直流電圧が一定とみなせるほど十分に大きいものとし,損失のない理想的なチョッパとする。
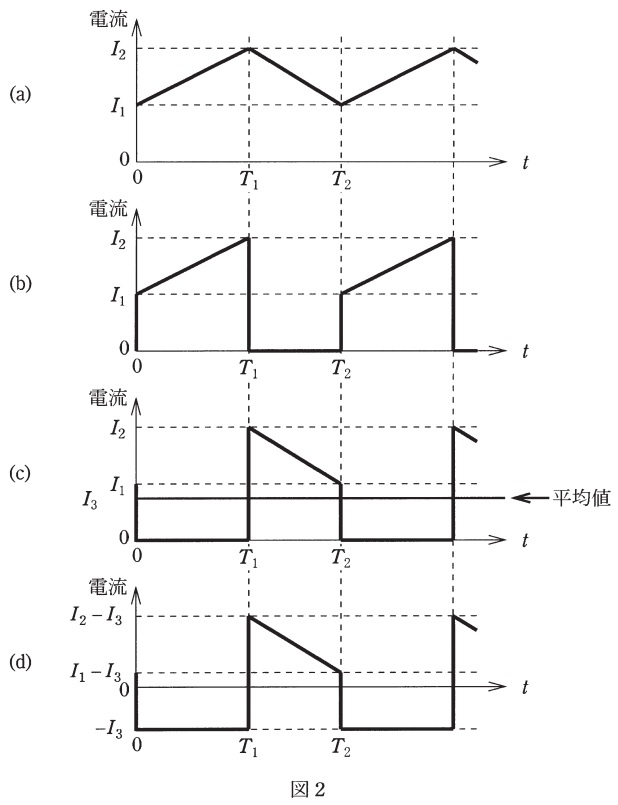
(1) 図1の昇降圧チョッパにおいて,トランジスタ\(Q_{1}\)が時刻\(0\)でターンオン,時刻\(T_{1}\)でターンオフ,時刻\(T_{2}\)でターンオンするという1周期の動作を繰り返しているとする。図2は,この昇降圧チョッパの各部の電流波形を示す。図1に示す各部の電流\(i_{\mathrm {S}}\),\(i_{\mathrm {D}}\),\(i_{\mathrm {L}}\)及び\(i_{\mathrm {C}}\)の波形を図2の波形の中から選び,その記号で答えよ。
(2) 図2から\(T_{1}\)及び\(T_{2}\)を用いて通流率(時比率)\(\alpha \)を表せ。
(3) 図1の出力電圧\(V_{1}\)を入力電圧\(E_{1}\)及び通流率\(\alpha \)を用いて表せ。
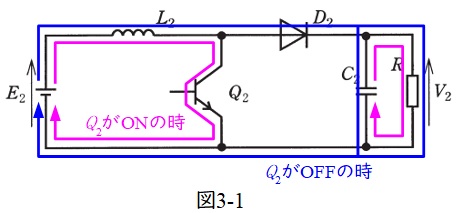
(4) 図3の昇圧チョッパにおいて,トランジスタ\(Q_{2}\)が時刻\(0\)でターンオン,時刻\(T_{\mathrm {a}}\)でターンオフ,時刻\(T_{\mathrm {b}}\)でターンオンするという1周期の動作を繰り返しているとする。このときの通流率(時比率)\(\beta \)を\(T_{\mathrm {a}}\)及び\(T_{\mathrm {b}}\)を用いて表し,出力電圧\(V_{2}\)を入力電圧\(E_{2}\)及び通流率\(\beta \)を用いて表せ。
(5) 図1の昇降圧チョッパと図3の昇圧チョッパとにおいて,同じ入力電圧で同じ通流率のときに出力電圧がより高いのはどちらのチョッパであるか。また,その理由を示せ。
【ワンポイント解説】
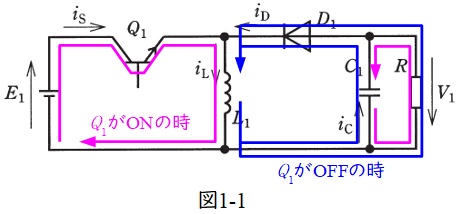
参考書でチョッパの概念を理解していれば,計算も難しくなく(5)の解答もある程度想像できるので比較的易しい問題と言えると思います。パワーエレクトロニクスの問題は下図のようにターンオン時とターンオフ時にどのように電流が流れるかを把握することが第一のステップとなります。本問の場合はこれができれば8割方解けたと言えると思います。
【関連する「電気の神髄」記事】
【解答】
(1)\(i_{\mathrm {S}}\),\(i_{\mathrm {D}}\),\(i_{\mathrm {L}}\)及び\(i_{\mathrm {C}}\)の波形
図1-1より,\(i_{\mathrm {S}}\)は\(Q_{1}\)がターンオンの時導通し,ターンオフの時\(0\)となる。よって,この条件に合致するのは(b)となる。
\(i_{\mathrm {D}}\)はターンオフの時導通し,ターンオンの時\(0\)となる。よって,この条件に合致するのは(c)となる。
\(i_{\mathrm {L}}\)はターンオンとターンオフで電流の向きが変わらないので(a)となる。
\(i_{\mathrm {C}}\)はターンオンとターンオフで電流の向きが反転するので(d)となる。
(2)通流率(時比率)\(\alpha \)を\(T_{1}\)及び\(T_{2}\)を用いて表す
通流率は\(\displaystyle \frac {ターンオンの時間}{ターンオンの時間+ターンオフの時間}\)で表すことができるので,
\[
\begin{eqnarray}
\alpha &=&\frac {T_{1}}{T_{1}+\left( T_{2} -T_{1}\right) } \\[ 5pt ]
&=&\frac {T_{1}}{T_{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)出力電圧\(V_{1}\)を入力電圧\(E_{1}\)及び通流率\(\alpha \)を用いて表す
\(L_{1}\)において,ターンオン時に蓄えられるエネルギーとターンオフ時に消費されるエネルギーは等しいので,
\[
\begin{eqnarray}
E_{1}T_{1} &=&V_{1}\left( T_{2} -T_{1}\right) \\[ 5pt ]
\end{eqnarray}
\]
となる。(2)より\(T_{1}=\alpha T_{2}\)であるから,
\[
\begin{eqnarray}
E_{1}\alpha T_{2} &=&V_{1}\left( T_{2} -\alpha T_{2}\right) \\[ 5pt ]
E_{1}\alpha &=&V_{1}\left( 1 -\alpha \right) \\[ 5pt ]
V_{1} &=&\frac {\alpha }{1 -\alpha }E_{1} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)通流率(時比率)\(\beta \)を\(T_{\mathrm {a}}\)及び\(T_{\mathrm {b}}\)を用いて表し,出力電圧\(V_{2}\)を入力電圧\(E_{2}\)及び通流率\(\beta \)を用いて表す
(2)と同様に通流率\(\beta \)は,
\[
\begin{eqnarray}
\beta &=&\frac {T_{\mathrm {a}}}{T_{\mathrm {b}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
リアクトル\(L_{2}\)において,ターンオン時に蓄えられるエネルギーとターンオフ時に消費されるエネルギーは等しいので,
\[
\begin{eqnarray}
E_{2}T_{\mathrm {a}} &=&V_{2}\left( T_{\mathrm {b}} -T_{\mathrm {a}}\right) -E_{2}\left( T_{\mathrm {b}} -T_{\mathrm {a}}\right) \\[ 5pt ]
0 &=&V_{2}\left( T_{\mathrm {b}} -T_{\mathrm {a}}\right) -E_{2}T_{\mathrm {b}} \\[ 5pt ]
V_{2}&=&\frac {T_{\mathrm {b}}}{T_{\mathrm {b}} -T_{\mathrm {a}}}E_{2} \\[ 5pt ]
&=&\frac {1}{1 -\frac {T_{\mathrm {a}}}{T_{\mathrm {b}}}}E_{2} \\[ 5pt ]
&=&\frac {1}{1 -\beta }E_{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)図1の昇降圧チョッパと図3の昇圧チョッパとにおいて,同じ入力電圧で同じ通流率のときに出力電圧がより高いのはどちらのチョッパであるか
題意より\(E_{1}=E_{2}\),\(\alpha =\beta \)であるから,
\[
\begin{eqnarray}
\frac {V_{2}}{V_{1}} &=&\frac {\displaystyle \frac {1}{1 -\beta }E_{2}}{\displaystyle \frac {\alpha }{1 -\alpha }E_{1}} \\[ 5pt ]
&=&\frac {\displaystyle \frac {1}{1 -\alpha }E_{1}}{\displaystyle \frac {\alpha }{1 -\alpha }E_{1}} \\[ 5pt ]
&=&\frac {1}{\alpha} > 1 \\[ 5pt ]
\end{eqnarray}
\]
となるので,出力電圧は昇圧チョッパの方が高くなる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは