《機械・制御》〈パワーエレクトロニクス〉[H29:問3]単相ダイオード整流器に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

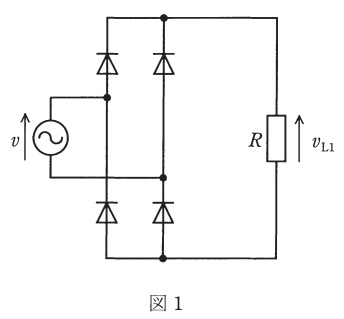
図1～3のように単相ダイオード整流器を\( \ 200 \ \mathrm {V} \ \)，\( \ 50 \ \mathrm {Hz} \ \)の交流電源\( \ v \ \)に接続する。それぞれの回路には，負荷として\( \ R=100 \ \Omega \ \)の抵抗器を接続する。図2のコンデンサの静電容量及び図3のインダクタのインダクタンスは十分に大きく，コンデンサの電圧リプル及びインダクタの電流リプルは無視できる。また，ダイオード，コンデンサ及びインダクタの損失はないものとする。回路が動作してから十分に時間が経過しているものとして，次の問に答えよ。

(1)　図1の負荷電圧\( \ v_{\mathrm {L1}} \ \)の平均値\( \ V_{\mathrm {L1}} \ \)を求めよ。

(2)　図1の負荷抵抗器\( \ R \ \)の消費電力の平均値\( \ P_{\mathrm {L1}} \ \)を求めよ。

(3)　図2の負荷電圧\( \ v_{\mathrm {L2}} \ \)の平均値\( \ V_{\mathrm {L2}} \ \)を求めよ。

(4)　図2の負荷抵抗器\( \ R \ \)の消費電力の平均値\( \ P_{\mathrm {L2}} \ \)を求めよ。

(5)　図3の負荷電圧\( \ v_{\mathrm {L3}} \ \)の平均値\( \ V_{\mathrm {L3}} \ \)を求めよ。

(6)　図3の負荷抵抗器\( \ R \ \)の消費電力の平均値\( \ P_{\mathrm {L3}} \ \)を求めよ。

【ワンポイント解説】

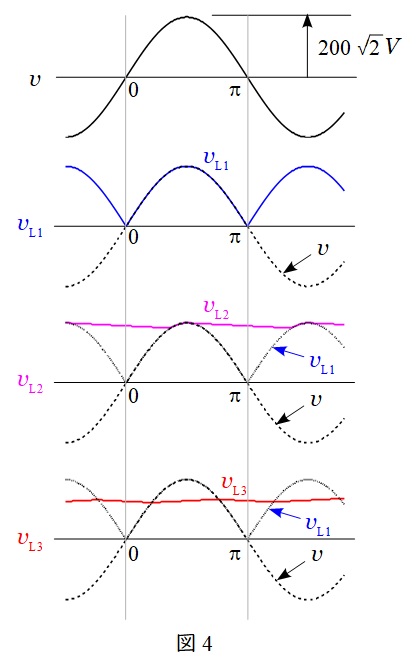
本問はパワーエレクトロニクスの基本を理解するのに最適な問題ですが，一方で受験生には「本当にこれで良いのだろうか」と悩ませる問題です。問題文から，図4のような波形を描ければ完璧です。本問を通じて，各整流回路の違いを理解しておきましょう。

【関連する「電気の神髄」記事】

　　単相全波整流回路

【解答】

(1)
図1の回路において，出力波形の\( \ v_{\mathrm {L1}} \ \)は図4の青線のように描けるので，その平均値\( \ V_{\mathrm {L1}} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {L1}} &=& \frac {1}{\pi}\int ^{\pi}_{0}{v_{\mathrm {L1}}\mathrm {d}\theta} \\[ 5pt ] &=& \frac {1}{\pi}\int ^{\pi}_{0}{200\sqrt {2}\sin \theta \mathrm {d}\theta} \\[ 5pt ] &=& \frac {200\sqrt {2}}{\pi}\left[ -\cos \theta \right] ^{\pi}_{0} \\[ 5pt ] &=& \frac {200\sqrt {2}}{\pi}\times 2 \\[ 5pt ] &≒& 180.06　→　180 \ [\mathrm {V}] \end{eqnarray}
\] となる。

(2)
\( \ v_{\mathrm {L1}} \ \)の実効値\( \ V^{\prime }_{\mathrm {L1}} \ \)は，
\[
\begin{eqnarray}
V^{\prime }_{\mathrm {L1}}&=&\frac {200\sqrt {2}}{\sqrt {2}} \\[ 5pt ] &=&200 \ [\mathrm {V}] \\[ 5pt ] \end{eqnarray}
\] であるから，消費電力の平均値\( \ P_{\mathrm {L1}} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {L1}} &=& \frac {{V ^{’} _{\mathrm {L1}}}^{2} }{R} \\[ 5pt ] &=& \frac {200^{2}}{100}\\[ 5pt ] &=&400 \ [\mathrm {W}] \end{eqnarray}
\] と求められる。

(3)
図2の回路において，出力波形の\( \ v_{\mathrm {L2}} \ \)は図4の桃線のように描ける。題意より，コンデンサの容量が十分に大きいので，\( \ v_{\mathrm {L2}} \ \)は\( \ v \ \)の最大値\( \ 200\sqrt {2}V \ \)から変化なく，ほぼ一定と見なせる。よって，その平均値\( \ V_{\mathrm {L2}} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {L2}} &=& 200\sqrt {2} \\[ 5pt ] &≒&282.84　→　283 \ [\mathrm {V}] \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)
図4の通り，出力一定であるため，電圧の実効値も\( \ V_{\mathrm {L2}} \ \)と等しくなる。よって，消費電力の平均値\( \ P_{\mathrm {L2}} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {L2}} &=& \frac {{V_{\mathrm {L2}}}^{2} }{R} \\[ 5pt ] &=& \frac {\left( 200\sqrt {2}\right) ^{2}}{100} \\[ 5pt ] &=& 800 \ [\mathrm {W}] \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)
図3の回路において，出力波形の\( \ v_{\mathrm {L3}} \ \)は図4の赤線のように描ける。題意より，インダクタの容量が十分に大きいので，\( \ v_{\mathrm {L3}} \ \)は\( \ v_{\mathrm {L1}} \ \)の平均値\( \ V_{\mathrm {L1}} \ \)とほぼ同値で一定となる。よってその平均値\( \ V_{\mathrm {L3}} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {L3}}&=&V_{\mathrm {L1}} \\[ 5pt ] &=&180.06　→　180 \ [\mathrm {V}] \\[ 5pt ] \end{eqnarray}
\] と求められる。

(6)
図4の通り，出力一定であるため，電圧の実効値も\( \ V_{\mathrm {L3}} \ \)と等しくなる。よって，消費電力の平均値\( \ P_{\mathrm {L3}} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {L3}} &=& \frac {{V_{\mathrm {L3}}}^{2} }{R} \\[ 5pt ] &=& \frac {180.06^{2}}{100} \\[ 5pt ] &≒& 324.22　→　324 \ [\mathrm {W}] \\[ 5pt ] \end{eqnarray}
\] と求められる。