《理論》〈電子回路〉[H29:問8]演算増幅器を用いた回路に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★☆☆☆☆（易しい）

次の文章は，演算増幅器を用いた回路に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。ただし，演算増幅器は理想的であるとする。

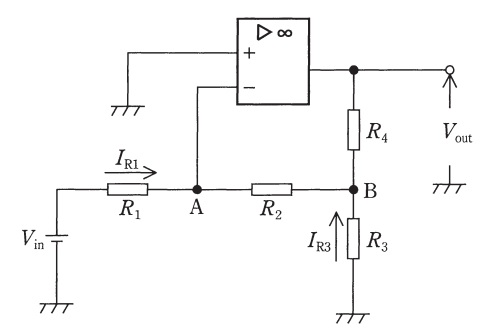
負帰還がかけられた演算増幅器の入力端子間の電位差は零となるため，$ \ \mathrm{A} \ $点の電位は零となる。いま，回路に正の入力電圧$ \ V_{\mathrm{in}} \ $が入力されるとすると，$ \ R_{\mathrm{1}} \ $を流れる電流$ \ I_{\mathrm{R1}} \ $は$ \ \fbox {　（１）　} \ $となる。この電流は全て$ \ R_{2} \ $を流れるため，$ \ \mathrm{B} \ $点の電位は$ \ \fbox {　（２）　} \ $となる。このとき，$ \ R_{3} \ $には接地された端子から$ \ \mathrm{B} \ $点に向かって$ \ \fbox {　（３）　} \ $で表される電流$ \ I_{\mathrm{R3}} \ $が流れる。$ \ R_{4} \ $を流れる電流は$ \ I_{\mathrm{R1}} \ $と$ \ I_{\mathrm{R3}} \ $の和になっているため，$ \ R_{4} \ $の両端に現れる電圧の大きさは$ \ \fbox {　（４）　} \ $となる。出力端子の電圧$ \ V_{\mathrm{out}} \ $は$ \ \mathrm{B} \ $点の電位から$ \ \fbox {　（４）　} \ $だけ低い電位となるため，この回路の電圧利得$ \ \displaystyle \frac {V_{\mathrm{out}}}{V_{\mathrm{in}}} \ $は$ \ \fbox {　（５）　} \ $となる。

〔問8の解答群〕
\[
\begin{eqnarray}
&（イ）&　-\frac {1}{R_{1}}\left[ R_{2}-R_{4}\left( 1+\frac {R_{2}}{R_{3}}\right) \right]　　　&（ロ）&　\frac {R_{2}}{R_{1} R_{3}}V_{\mathrm{in}} \\[ 5pt ] &（ハ）&　-\frac {R_{2}}{R_{1}}V_{\mathrm{in}} 　　　&（ニ）&　\frac {V_{\mathrm{out}}-V_{\mathrm{in}}}{R_{1}+R_{2}+R_{4}} \\[ 5pt ] &（ホ）&　\frac {R_{4}}{R_{1}}\left( \frac {R_{2}}{R_{3}}+1\right) V_{\mathrm{in}}　　　&（ヘ）&　-\frac {1}{R_{1}}\left[ R_{2}+R_{4}\left( 1+\frac {R_{2}}{R_{3}}\right) \right] \\[ 5pt ] &（ト）&　-\frac {R_{2}}{R_{3}}V_{\mathrm{in}}　　　&（チ）&　\frac {V_{\mathrm{in}}}{R_{1}+R_{2}+R_{3}}　 \\[ 5pt ] &（リ）&　\frac {R_{1}}{R_{2}}+R_{4}\left( \frac {1}{R_{3}}+\frac {1}{R_{1}}\right)　　　&（ヌ）&　\frac {V_{\mathrm{in}}}{R_{3}} \\[ 5pt ] &（ル）&　R_{4}\left( \frac {1}{R_{3}}+\frac {1}{R_{1}}\right) V_{\mathrm{in}}　　　&（ヲ）&　\frac {R_{1}}{R_{2} R_{3}}V_{\mathrm{in}} \\[ 5pt ] &（ワ）&　\frac {R_{1}}{R_{2}}V_{\mathrm{in}}　　　&（カ）&　\frac {V_{\mathrm{in}}}{R_{1}}　\\[ 5pt ] &（ヨ）&　R_{4}\left( \frac {1}{R_{1}}+\frac {R_{1}}{R_{2}R_{3}}\right) V_{\mathrm{in}}
\end{eqnarray}
\]

【ワンポイント解説】

平成29年度の合格点を大きく引き上げたのではないかと思う問題です。オペアンプを使用していますが，実質的にはその中身を知らなくてもすべて問題文に書いてあります。電験二種を合格する受験生であれば，ぜひ完答したい問題です。本問に出てくるオペアンプの特徴のうち電験で理解しておくべき特徴は下記の通りです。ただし，本問の場合は知らなくても解けてしまいます。

1.理想的なオペアンプの特徴
１．電圧増幅率が無限大である。したがって，無限大でない有限数が出力される時，入力端子間の電圧は$0\mathrm {V}$(バーチャルショート)となる。
２．入力インピーダンスが無限大である。したがって入力端子に電流は流れない。
３．出力インピーダンスがゼロである。

【解答】

(1)解答：カ
$ \ R_{1} \ $を流れる電流$ \ I_{\mathrm{R1}} \ $はオームの法則から，
\[
\begin{eqnarray}
I_{\mathrm{R1}}&=&\frac {V_{\mathrm{in}}}{R_{1}} \\[ 5pt ] \end{eqnarray}
\] となる。

(2)解答：ハ
題意より，$ \ R_{2} \ $を流れる電流は$ \ I_{\mathrm{R1}} \ $であるから，$ \ \mathrm {B} \ $の電位$ \ V_{\mathrm{B}} \ $は，
\[
\begin{eqnarray}
V_{\mathrm{B}} &=& 0-R_{2}I_{\mathrm{R1}} \\[ 5pt ] &=& -\frac {R_{2}}{R_{1}}V_{\mathrm{in}} \\[ 5pt ] \end{eqnarray}
\] となる。

(3)解答：ロ
$ \ R_{3} \ $を流れる電流$ \ I_{\mathrm{R3}} \ $は，
\[
\begin{eqnarray}
I_{\mathrm{R3}} &=& \frac {0-V_{B}}{R_{3}} \\[ 5pt ] &=& \frac {\displaystyle \frac {R_{2}}{R_{1}} V_{\mathrm{in}}}{R_{3}} \\[ 5pt ] &=& \frac {R_{2}}{R_{1} R_{3}}V_{\mathrm{in}}
\end{eqnarray}
\] となる。

(4)解答：ホ
$ \ R_{4} \ $を流れる電流$ \ I_{\mathrm{R4}} \ $は，題意より，
\[
\begin{eqnarray}
I_{\mathrm{R4}} &=& I_{\mathrm{R1}}+I_{\mathrm{R3}} \\[ 5pt ] &=& \frac {V_{\mathrm{in}}}{R_{1}}+\frac {R_{2}}{R_{1} R_{3}}V_{\mathrm{in}} \\[ 5pt ] &=& \frac {1}{R_{1}}\left( 1+\frac {R_{2}}{R_{3}}\right) V_{\mathrm{in}}
\end{eqnarray}
\] であるから，$ \ R_{4} \ $の両端に現れる電圧の大きさ$ \ V_{\mathrm{R4}} \ $は，
\[
\begin{eqnarray}
V_{\mathrm{R4}} &=& R_{4}I_{\mathrm{R4}} \\[ 5pt ] &=& \frac {R_{4}}{R_{1}}\left( 1+\frac {R_{2}}{R_{3}}\right) V_{\mathrm{in}} \\[ 5pt ] &=& \frac {R_{4}}{R_{1}}\left( \frac {R_{2}}{R_{3}}+1\right) V_{\mathrm{in}}
\end{eqnarray}
\] と求められる。

(5)解答：ヘ
出力電圧$ \ V_{\mathrm{out}} \ $は，
\[
\begin{eqnarray}
V_{\mathrm{out}} &=& V_{\mathrm{B}}-V_{\mathrm{R4}} \\[ 5pt ] &=& -\frac {R_{2}}{R_{1}}V_{\mathrm{in}}-\frac {R_{4}}{R_{1}}\left( \frac {R_{2}}{R_{3}}+1\right) V_{\mathrm{in}} \\[ 5pt ] &=& -\frac {1}{R_{1}}\left[ R_{2}+R_{4}\left( 1+\frac {R_{2}}{R_{3}}\right) \right] V_{\mathrm{in}} \\[ 5pt ] \end{eqnarray}
\] ゆえに，
\[
\begin{eqnarray}
\frac {V_{\mathrm{out}}}{V_{\mathrm{in}}}&=&-\frac {1}{R_{1}}\left[ R_{2}+R_{4}\left( 1+\frac {R_{2}}{R_{3}}\right) \right] \\[ 5pt ] \end{eqnarray}
\] となる。