《理論》〈電気回路〉[R01:問6]直流電源と抵抗からなる回路の電流に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，直流電源と抵抗からなる回路の電流に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

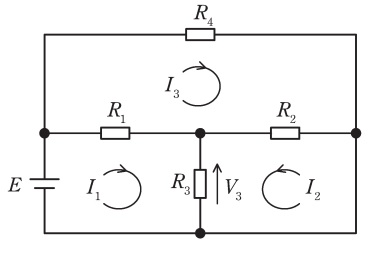
図の抵抗回路の閉路電流$ \ I_{1} \ $，$ \ I_{2} \ $，$ \ I_{3} \ $は，閉路方程式を解いて求めることができるが，以下の手順で求めることもできる。

a.$ \ I_{3} \ $は，$ \ R_{4} \ $の両端の電位差に注意すると，$ \ I_{3}= \ \fbox {　（１）　} \ $。

b.$ \ R_{3} \ $での電圧降下$ \ V_{3} \ $の式は，
\[
\begin{eqnarray}
V_{3} &=& \frac {1}{\displaystyle R_{1}+\frac {R_{2}R_{3}}{R_{2}+R_{3}}}\times \ \fbox {　（２）　} \ \times E \\[ 5pt ] \end{eqnarray}
\] となる。

c.$ \ I_{1} \ $，$ \ I_{2} \ $，$ \ I_{3} \ $を使うと，
\[
\begin{eqnarray}
E-V_{3} &=& R_{1}\left( \ \fbox {　（３）　} \ \right) \\[ 5pt ] V_{3} &=& R_{2}\left( \ \fbox {　（４）　} \ \right) \\[ 5pt ] \end{eqnarray}
\] である。
以上を利用すれば，
\[
\begin{eqnarray}
I_{1} &=& E\left( \frac {1}{R_{4}}+\frac {R_{2}+R_{3}}{R_{1}R_{2}+R_{2}R_{3}+R_{3}R_{1}}\right) \\[ 5pt ] I_{2} &=& \ \fbox {　（５）　} \\[ 5pt ] \end{eqnarray}
\] が得られる。

〔問6の解答群〕
\[
\begin{eqnarray}
&（イ）&　E\left( -\frac {1}{R_{4}}-\frac {R_{3}}{R_{1}R_{2}+R_{2}R_{3}+R_{3}R_{1}}\right)　　　&（ロ）&　I_{1}-I_{3}　　　&（ハ）&　-I_{2}-I_{3} \\[ 5pt ] &（ニ）&　\frac {R_{1}R_{2}}{R_{1}+R_{2}}　　　&（ホ）&　I_{3}+I_{1}　　　&（ヘ）&　\frac {R_{2}R_{3}}{R_{2}+R_{3}} \\[ 5pt ] &（ト）&　E\left( -\frac {R_{3}}{R_{1}R_{2}+R_{2}R_{3}+R_{3}R_{1}}\right)　　　&（チ）&　\frac {R_{2}R_{4}}{R_{2}+R_{4}}　　　　&（リ）&　\frac {E}{R_{1}+R_{2}+R_{4}} \\[ 5pt ] &（ヌ）&　I_{2}　　　&（ル）&　\frac {E}{R_{1}+R_{2}}　　　&（ヲ）&　I_{3}-I_{1} \\[ 5pt ] &（ワ）&　E\left( \frac {1}{R_{4}}-\frac {R_{3}}{R_{1}R_{2}+R_{2}R_{3}+R_{3}R_{1}}\right)　　　&（カ）&　\frac {E}{R_{4}}　　　&（ヨ）&　I_{1} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

キルヒホッフの法則や分圧の法則等の基本法則を用いて解く問題です。扱っている公式は基本公式のみですが，問題を読み解く能力と計算能力が問われる問題となっており，電流の向きに注意して解く必要があります。

【解答】

(1)解答：カ
$ \ R_{4} \ $には電源電圧$ \ E \ $がかかるので，
\[
\begin{eqnarray}
I_{3} &=& \frac {E}{R_{4}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ヘ
$ \ R_{2} \ $と$ \ R_{3} \ $は並列回路となっているので，その合成抵抗$ \ R_{23} \ $は，
\[
\begin{eqnarray}
R_{23} &=& \frac {R_{2}R_{3}}{R_{2}+R_{3}} \\[ 5pt ] \end{eqnarray}
\] となり，問題図は図1のように書き換えることができる。

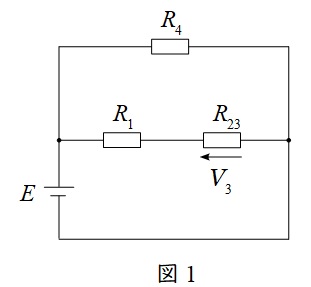
図1において分圧の法則より，$ \ V_{3} \ $は，
\[
\begin{eqnarray}
V_{3} &=& \frac {R_{23}}{R_{1}+R_{23}} \times E \\[ 5pt ] &=& \frac {\displaystyle \frac {R_{2}R_{3}}{R_{2}+R_{3}}}{\displaystyle R_{1}+\frac {R_{2}R_{3}}{R_{2}+R_{3}}}\times E \\[ 5pt ] &=& \frac {1}{\displaystyle R_{1}+\frac {R_{2}R_{3}}{R_{2}+R_{3}}}\times \frac {R_{2}R_{3}}{R_{2}+R_{3}}\times E \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ロ
問題図より，$ \ E-V_{3} \ $は$ \ R_{1} \ $にかかる電圧であり，$ \ R_{1} \ $に流れる電流は$ \ I_{1}-I_{3} \ $であるから，
\[
\begin{eqnarray}
E-V_{3} &=& R_{1}\left( I_{1}-I_{3} \right) \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ハ
問題図より，$ \ R_{2} \ $の電圧降下は$ \ V_{3} \ $であり，$ \ R_{2} \ $を流れる電流は$ \ -I_{2}-I_{3} \ $であるから，
\[
\begin{eqnarray}
V_{3} &=& R_{2}\left( -I_{2}-I_{3} \right) \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：イ
(4)の解答式より，
\[
\begin{eqnarray}
V_{3} &=& R_{2}\left( -I_{2}-I_{3} \right) \\[ 5pt ] \frac {V_{3}}{R_{2}}&=& -I_{2}-I_{3} \\[ 5pt ] I_{2}&=& -I_{3}-\frac {V_{3}}{R_{2}} \\[ 5pt ] \end{eqnarray}
\] であるから，(1)及び(2)の解答式を代入すると，
\[
\begin{eqnarray}
I_{2}&=& -\frac {E}{R_{4}}-\frac {1}{R_{2}}\times \frac {\displaystyle \frac {R_{2}R_{3}}{R_{2}+R_{3}}}{\displaystyle R_{1}+\frac {R_{2}R_{3}}{R_{2}+R_{3}}}\times E \\[ 5pt ] &=& -\frac {E}{R_{4}}-\frac {\displaystyle \frac {R_{3}}{R_{2}+R_{3}}}{\displaystyle R_{1}+\frac {R_{2}R_{3}}{R_{2}+R_{3}}}\times E \\[ 5pt ] &=& -\frac {E}{R_{4}}-\frac {\displaystyle \frac {R_{3}}{R_{2}+R_{3}}}{\displaystyle \frac {R_{1}\left( R_{2}+R_{3}\right) +R_{2}R_{3}}{R_{2}+R_{3}}}\times E \\[ 5pt ] &=& -\frac {E}{R_{4}}-\frac {R_{3}}{R_{1}R_{2}+R_{3}R_{1} +R_{2}R_{3}}\times E \\[ 5pt ] &=& E\left( -\frac {1}{R_{4}}-\frac {R_{3}}{R_{1}R_{2}+R_{2}R_{3}+R_{3}R_{1}}\right) \\[ 5pt ] \end{eqnarray}
\] と求められる。