《理論》〈電子理論〉[R01:問7]磁界中の電子の運動に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★☆☆☆☆（易しい）

次の文章は，磁界中の電子の運動に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

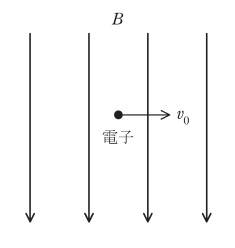
図のように，磁束密度$ \ B\left( ＞0\right) \ $の一様な磁界に直角に速度$ \ v_{0}\left( ＞0\right) \ $で電子(質量$ \ m \ $，電荷$ \ -e \ $，$ \ e＞0 \ $)が運動している。このとき電子は磁界からローレンツ力を受ける。その力の向きは電子の進行方向に直角で$ \ \fbox {　（１）　} \ $の方向であり，その大きさは$ \ F= \ \fbox {　（２）　} \ $である。電子はこの力を向心力として半径$ \ r \ $の円運動をすることから，$ \ r= \ \fbox {　（３）　} \ $となる。また，電子が回転する角周波数は$ \ \omega = \ \fbox {　（４）　} \ $である。ここに角周波数が$ \ \omega \ $と等しい振動電界を外部から印加することにより，電子を効率よく加速したり減速したりすることができる。電子が加速された場合には，電子の速度$ \ v_{0} \ $が増大することから，円運動の半径は増大する。このとき，電子の円運動の角周波数$ \ \omega \ $の大きさは$ \ \fbox {　（５）　} \ $。この現象はサイクロトロン共鳴と呼ばれ，高密度プラズマの生成や，固体の有効質量の測定などに応用されている。

〔問7の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {eB}{m}　　　&（ロ）&　増大する　　　&（ハ）&　\frac {mv_{0}^{2}}{eB} \\[ 5pt ] &（ニ）&　減少する　　　&（ホ）&　\frac {mv_{0}}{eB}　　　&（ヘ）&　\frac {eB}{v_{0}} \\[ 5pt ] &（ト）&　\frac {m}{eB}　　　&（チ）&　ev_{0}^{2}B　　　&（リ）&　紙面表から裏へ \\[ 5pt ] &（ヌ）&　紙面裏から表へ　　　&（ル）&　\frac {ev_{0}B}{m}　　　&（ヲ）&　変わらない \\[ 5pt ] &（ワ）&　ev_{0}B　　　&（カ）&　磁界 \ B \ と逆向き　　　&（ヨ）&　\frac {eB}{2\pi m} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

磁界中の電子の運動に関する問題で，１種～３種まで非常に出題されやすい頻出項目となっています。

1.フレミングの左手の法則
中指を電流の向き，人差し指を磁界の向きに合わせると，親指の方向に力が働くという法則で，頭文字を取って「電磁力」と覚えます。
磁束密度の大きさ$ \ B \ $，電流の大きさ$ \ I \ $，直線状導体の長さを$ \ l \ $とすると，導体に発生する電磁力$ \ F \ $は，
\[
\begin{eqnarray}
F &=&BIl \\[ 5pt ] \end{eqnarray}
\] となります。
また，電荷$ \ -e \ $の電子が速度$ \ v \ $で動いている時，電子に働く力$ \ F \ $の大きさは，
\[
\begin{eqnarray}
F &=&evB \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)解答：ヌ
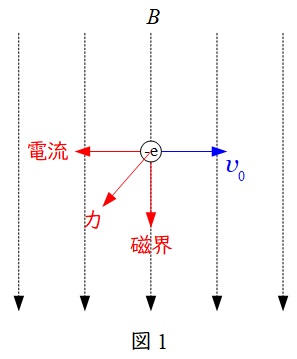
電子の動く向きは電流の向きと逆になるので，それに注意すると，ワンポイント解説「1.フレミングの左手の法則」より，電子の動く向きは図1のようになる。したがって，電子に働く力は紙面裏から表に向かう方向となる。

(2)解答：ワ
ワンポイント解説「1.フレミングの左手の法則」より電子に働くローレンツ力$ \ F \ $は，
\[
\begin{eqnarray}
F &=&ev_{0}B \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ホ
円運動の向心力は$ \ \displaystyle F=\frac {mv_{0}^{2}}{r} \ $であり，それがローレンツ力$ \ F \ $と等しいので，
\[
\begin{eqnarray}
\frac {mv_{0}^{2}}{r} &=&ev_{0}B \\[ 5pt ] \end{eqnarray}
\] となり，整理すると，
\[
\begin{eqnarray}
\frac {mv_{0}}{r} &=&eB \\[ 5pt ] r&=&\frac {mv_{0}}{eB} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：イ
角周波数$ \ \omega \ $は，$ \ \displaystyle \frac {v_{0}}{r} \ $であるから，
\[
\begin{eqnarray}
\omega &=&\frac {v_{0}}{r} \\[ 5pt ] &=&v_{0}\times \frac {eB}{mv_{0}} \\[ 5pt ] &=&\frac {eB}{m} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ヲ
(4)解答式より，角周波数$ \ \omega \ $は$ \ v_{0} \ $に依存しないので，角周波数の大きさは変わらない。