Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
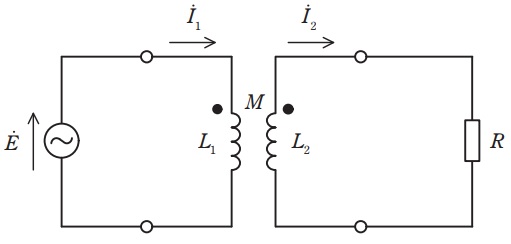
次の文章は,変成器を含む交流回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。なお,図の回路において電源の電圧は\( \ \dot E \ \),角周波数は\( \ \omega \ \),変成器の一次側コイルのインダクタンスは\( \ L_{1} \ \),二次側コイルのインダクタンスは\( \ L_{2} \ \),相互インダクタンスは\( \ M>0 \ \)であり,変成器の巻線抵抗は無視するものとする。
図の回路の一次側と二次側において,以下の回路方程式
\[
\begin{eqnarray}
\dot E &=& \ \fbox { (1) } \ -\mathrm {j}\omega M {\dot I}_{2} \\[ 5pt ]
0 &=& \ \fbox { (2) } \ +\left( R+\mathrm {j}\omega L_{2}\right) {\dot I}_{2} \\[ 5pt ]
\end{eqnarray}
\]
が成り立つ。
したがって,二次側電流\( \ {\dot I}_{2} \ \)と一次側電流\( \ {\dot I}_{1} \ \)の関係は,
\[
\begin{eqnarray}
{\dot I}_{2} &=& \ \fbox { (3) } \ \\[ 5pt ]
\end{eqnarray}
\]
と表せる。
以上より,図の回路の一次側から見たインピーダンス\( \ {\dot Z} \ \)は,
\[
\begin{eqnarray}
{\dot Z} &=& \mathrm {j}\omega L_{1}+ \ \fbox { (4) } \ \\[ 5pt ]
\end{eqnarray}
\]
となる。
また,図の回路において,二次側の抵抗\( \ R=\infty \ \)とすれば,回路の一次側電流\( \ {\dot I}_{1}= \ \fbox { (5) } \ \ \)となる。
〔問5の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {\left( \omega M\right) ^{2}}{R+\mathrm {j}\omega L_{1}} &(ロ)& \frac {\dot E}{\mathrm {j}\omega L_{2}} &(ハ)& \frac {\left( \omega M\right) ^{2}}{R+\mathrm {j}\omega L_{2}} \\[ 5pt ]
&(ニ)& \frac { \mathrm {j}\omega M}{R+\mathrm {j}\omega L_{1}}{\dot I}_{1} &(ホ)& \mathrm {j}\omega L_{1}{\dot I}_{1} &(ヘ)& \frac {\dot E}{\mathrm {j}\omega M} \\[ 5pt ]
&(ト)& \frac {\left( \omega M\right) ^{2}}{R+\mathrm {j}\omega M} &(チ)& -\mathrm {j}\omega M{\dot I}_{1} &(リ)& \frac {\dot E}{\mathrm {j}\omega L_{1}} \\[ 5pt ]
&(ヌ)& \frac { \mathrm {j}\omega M}{R+\mathrm {j}\omega M}{\dot I}_{1} &(ル)& \mathrm {j}\omega L_{1}{\dot I}_{2} &(ヲ)& \frac { \mathrm {j}\omega M}{R+\mathrm {j}\omega L_{2}}{\dot I}_{1} \\[ 5pt ]
&(ワ)& \mathrm {j}\omega M{\dot I}_{2} &(カ)& -\mathrm {j}\omega M{\dot I}_{2} &(ヨ)& -\mathrm {j}\omega L_{1}{\dot I}_{1} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
変成器を含む交流回路の計算に関する問題です。
変成器の電気回路での取り扱いを理解しておけば,完答を目指せる問題となります。
本問では\( \ \fbox { (1) } \ \)の空欄の式が磁束が強め合うのか弱め合うのかのヒントになっていますが,基本的には回路図を見ただけで判断できるになる必要があります。
以下の内容を必ず理解しておくようにしましょう。
1.変成器の和動接続及び差動接続
電気回路ではコイルの巻き方を指定するため「●」の記号を用いて示します。「●」の向き及び電流の流れる方向により,磁束を強め合う接続(和動接続)と磁束を弱め合う接続(差動接続)が変わります。
①磁束が強め合う接続(和動接続)
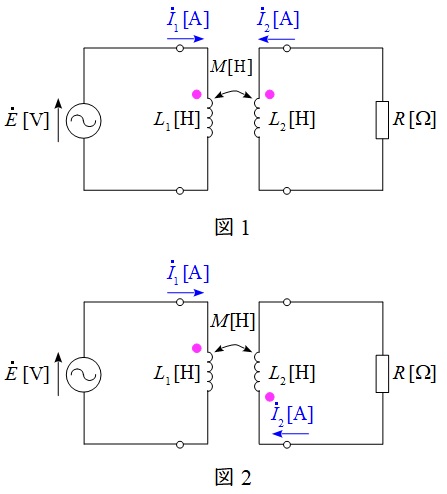
図1及び図2のような接続の場合,磁束は強め合うことになり,図1及び図2の例では一次側二次側においてそれぞれ以下の関係式が成り立ちます。
どちらも「●」方向から電流が流入もしくは流出しているというところから判断します。
\[
\begin{eqnarray}
\dot E &=& \mathrm {j}\omega L_{1} {\dot I}_{1}+\mathrm {j}\omega M {\dot I}_{2} \\[ 5pt ]
0 &=& \mathrm {j}\omega M {\dot I}_{1}+\left( R+\mathrm {j}\omega L_{2}\right) {\dot I}_{2} \\[ 5pt ]
\end{eqnarray}
\]
②磁束が弱め合う接続(差動接続)
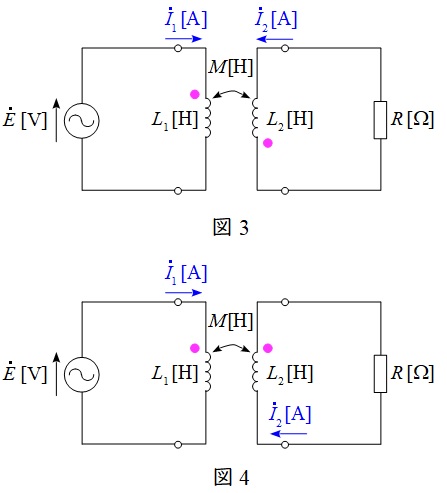
図3及び図4のような接続の場合,磁束は弱め合うことになり,図3及び図4の例では一次側二次側においてそれぞれ以下の関係式が成り立ちます。
一方が「●」方向から電流が流入し,もう一方が「●」方向から電流が流出しているというところから判断します。
\[
\begin{eqnarray}
\dot E &=& \mathrm {j}\omega L_{1} {\dot I}_{1}-\mathrm {j}\omega M {\dot I}_{2} \\[ 5pt ]
0 &=& -\mathrm {j}\omega M {\dot I}_{1}+\left( R+\mathrm {j}\omega L_{2}\right) {\dot I}_{2} \\[ 5pt ]
\end{eqnarray}
\]
【解答】
(1)解答:ホ
ワンポイント解説「1.変成器の和動接続及び差動接続」の通り,問題図は差動接続であるため,一次側の関係式は,
\[
\begin{eqnarray}
\dot E &=&\mathrm {j}\omega L_{1}{\dot I}_{1} -\mathrm {j}\omega M {\dot I}_{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:チ
(1)と同様に,二次側の関係式は,
\[
\begin{eqnarray}
0 &=& -\mathrm {j}\omega M{\dot I}_{1} +\left( R+\mathrm {j}\omega L_{2}\right) {\dot I}_{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ヲ
(2)解答式を\( \ {\dot I}_{2} \ \)について整理すると,
\[
\begin{eqnarray}
0 &=& -\mathrm {j}\omega M{\dot I}_{1} +\left( R+\mathrm {j}\omega L_{2}\right) {\dot I}_{2} \\[ 5pt ]
\left( R+\mathrm {j}\omega L_{2}\right) {\dot I}_{2}&=& \mathrm {j}\omega M{\dot I}_{1} \\[ 5pt ]
{\dot I}_{2}&=& \frac { \mathrm {j}\omega M}{R+\mathrm {j}\omega L_{2}}{\dot I}_{1} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ハ
(3)解答式を(1)解答式に代入して整理すると,
\[
\begin{eqnarray}
\dot E &=&\mathrm {j}\omega L_{1}{\dot I}_{1} -\mathrm {j}\omega M {\dot I}_{2} \\[ 5pt ]
&=&\mathrm {j}\omega L_{1}{\dot I}_{1} -\mathrm {j}\omega M \cdot \frac { \mathrm {j}\omega M}{R+\mathrm {j}\omega L_{2}}{\dot I}_{1} \\[ 5pt ]
&=&\mathrm {j}\omega L_{1}{\dot I}_{1} + \frac { \left( \omega M\right) ^{2}}{R+\mathrm {j}\omega L_{2}}{\dot I}_{1} \\[ 5pt ]
&=&\left\{ \mathrm {j}\omega L_{1} + \frac { \left( \omega M\right) ^{2}}{R+\mathrm {j}\omega L_{2}}\right\} {\dot I}_{1} ・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ \displaystyle \dot Z=\frac {\dot E}{{\dot I}_{1}} \ \)であるから,
\[
\begin{eqnarray}
\frac {\dot E}{{\dot I}_{1}}&=&\mathrm {j}\omega L_{1} + \frac { \left( \omega M\right) ^{2}}{R+\mathrm {j}\omega L_{2}} \\[ 5pt ]
\dot Z&=&\mathrm {j}\omega L_{1} + \frac { \left( \omega M\right) ^{2}}{R+\mathrm {j}\omega L_{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:リ
①式を\( \ {\dot I}_{1} \ \)について整理すると,
\[
\begin{eqnarray}
\dot E&=&\left\{ \mathrm {j}\omega L_{1} + \frac { \left( \omega M\right) ^{2}}{R+\mathrm {j}\omega L_{2}}\right\} {\dot I}_{1} \\[ 5pt ]
{\dot I}_{1}&=&\frac {\dot E}{\displaystyle \mathrm {j}\omega L_{1} + \frac { \left( \omega M\right) ^{2}}{R+\mathrm {j}\omega L_{2}}} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ R=\infty \ \)とすれば,
\[
\begin{eqnarray}
{\dot I}_{1}&=&\frac {\dot E}{\displaystyle \mathrm {j}\omega L_{1} + 0} \\[ 5pt ]
&=&\frac {\dot E}{\mathrm {j}\omega L_{1}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは