《理論》〈電気及び電子計測〉[R04:問8]電流比較器による電力計の校正に関する計算問題

【問題】

【難易度】★☆☆☆☆（易しい）

次の文章は，電流比較器による電力計の校正に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。

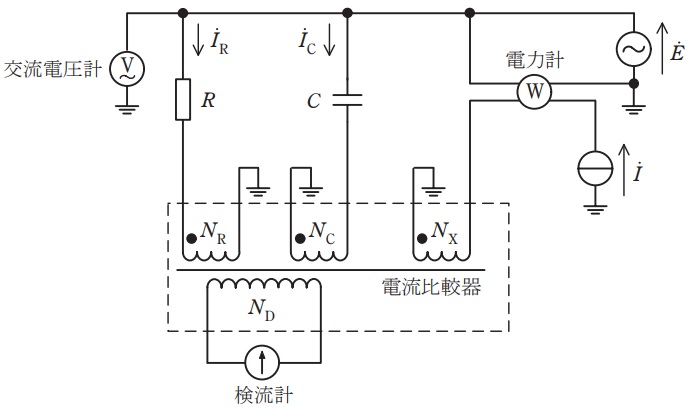
図は，校正対象の電力計と，電流比較器，抵抗\( \ R \ \)，静電容量\( \ C \ \)のコンデンサ，検流計及び交流電圧計から成る電力計の校正回路である。電流比較器は，鉄心や巻線の損失や漏れ磁束のない理想的なもので，\( \ N_{\mathrm {R}} \ \)，\( \ N_{\mathrm {C}} \ \)，\( \ N_{\mathrm {X}} \ \)及び\( \ N_{\mathrm {D}} \ \)は各巻線の巻数を表し，\( \ N_{\mathrm {R}} \ \)，\( \ N_{\mathrm {C}} \ \)及び\( \ N_{\mathrm {X}} \ \)は可変である。

電力計の校正の手順及び原理は次のとおりである。

まず，角周波数が等しく\( \ \omega \ \)である正弦波電圧\( \ \dot E \ \)及び正弦波電流\( \ \dot I \ \)を電力計及び校正回路に加える。次に，検流計が零を指すように\( \ N_{\mathrm {R}} \ \)，\( \ N_{\mathrm {C}} \ \)及び\( \ N_{\mathrm {X}} \ \)を調整し，さらに，\( \ \dot E \ \)の実効値\( \ \left| \dot E \right| \ \)を交流電圧計で測定する。

検流計が零を指すのは，各巻線を流れる電流によって生じる鉄心内の磁束が零になり，各巻線に生じる起電力が零になったときである。このとき，抵抗に流れる電流\( \ {\dot I}_{\mathrm {R}} \ \)は\( \ \fbox {　 （１） 　} \ \)，コンデンサに流れる電流\( \ {\dot I}_{\mathrm {C}} \ \)は\( \ \fbox {　 （２） 　} \ \)となる。また，各巻線の巻数と流れる電流の向きや，鉄心内の磁束が零であることを考慮すると，起磁力に関する等式\( \ \fbox {　 （３） 　} \ \)が成立する。

\( \ \fbox {　 （３） 　} \ \)を\( \ \dot I \ \)について解き，\( \ {\dot I}_{\mathrm {R}} \ \)及び\( \ {\dot I}_{\mathrm {C}} \ \)を代入する。さらに両辺に\( \ \dot E \ \)の共役複素数\( \ \overline E \ \)を乗じると次式が得られる。
\[
\begin{eqnarray}
\overline E\dot I&=& \ \fbox {　 （４） 　} \ -\mathrm {j} \ \fbox {　 （５） 　} \ \\[ 5pt ] \end{eqnarray}
\] なお，\( \ \fbox {　 （４） 　} \ \)及び\( \ \fbox {　 （５） 　} \ \)は，それぞれ，電力計へ入力される有効電力及び無効電力である。

以上のように，この校正回路は，既知の値(\( \ R \ \)，\( \ C \ \)，\( \ \omega \ \)及び巻数)と\( \ \left| \dot E \right| \ \)の測定値から有効電力及び無効電力を求め，電力計の校正を実現している。

〔問8の解答群〕
\[
\begin{eqnarray}
&（イ）&　N_{\mathrm {R}}{\dot I}_{\mathrm {R}}+N_{\mathrm {C}}{\dot I}_{\mathrm {C}}-N_{\mathrm {X}}\dot I=0　　　　　&（ロ）&　-\mathrm {j}\omega C \dot E　　　　　&（ハ）&　\frac {N_{\mathrm {X}}}{N_{\mathrm {C}}\omega C}\left| \dot E \right| ^{2} \\[ 5pt ] &（ニ）&　N_{\mathrm {R}}{\dot I}_{\mathrm {R}}-N_{\mathrm {C}}{\dot I}_{\mathrm {C}}-N_{\mathrm {X}}\dot I=0　　　　　&（ホ）&　R \dot E　　　　　&（ヘ）&　\frac {R}{\dot E} \\[ 5pt ] &（ト）&　\frac {N_{\mathrm {C}}\omega C}{N_{\mathrm {X}}}\left| \dot E \right|　　　　　&（チ）&　\mathrm {j}\omega C \dot E　　　　　&（リ）&　\frac {N_{\mathrm {C}}\omega C}{N_{\mathrm {X}}}\left| \dot E \right| ^{2} \\[ 5pt ] &（ヌ）&　\frac {N_{\mathrm {R}}}{N_{\mathrm {X}}R}\left| \dot E \right| ^{2}　　　　　&（ル）&　\frac {\dot E}{\mathrm {j}\omega C}　　　　　&（ヲ）&　\frac {\dot E}{R} \\[ 5pt ] &（ワ）&　N_{\mathrm {R}}{\dot I}_{\mathrm {R}}+N_{\mathrm {C}}{\dot I}_{\mathrm {C}}+N_{\mathrm {X}}\dot I=0　　　　　&（カ）&　\frac {N_{\mathrm {R}}}{N_{\mathrm {X}}R}\left| \dot E \right|　　　　　&（ヨ）&　\frac {N_{\mathrm {X}}R}{N_{\mathrm {R}}}\left| \dot E \right| ^{2} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

電力計の校正に関する問題です。
タイトルを見る限りやや難しそうに見える問題ですが，中身は電磁気や電気回路の基礎を理解していればそれほど難しくありません。
問題文に惑わされない様冷静に解くようにしましょう。

1.起磁力
起磁力\( \ F \ \mathrm {[A]} \ \)は磁気回路のオームの法則で出てくる力で，コイルの巻数\( \ N \ \)，コイルに流れる電流\( \ I \ \mathrm {[A]} \ \)とすると，\( \ F=NI \ \)で求められます。

【解答】

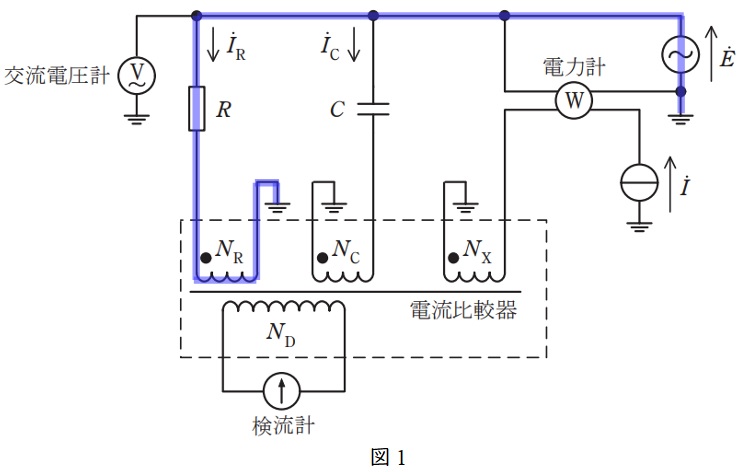
(1)解答：ヲ
図1の閉回路についてオームの法則を適用すると，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {R}}&=&\frac {\dot E}{R} \\[ 5pt ] \end{eqnarray}
\] と求められる。

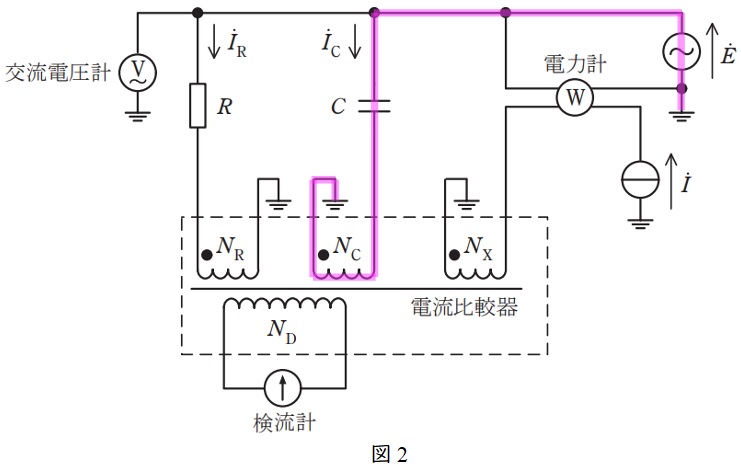
(2)解答：チ
図2の閉回路についてオームの法則を適用すると，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {C}}&=&\mathrm {j}\omega C \dot E \\[ 5pt ] \end{eqnarray}
\] と求められる。

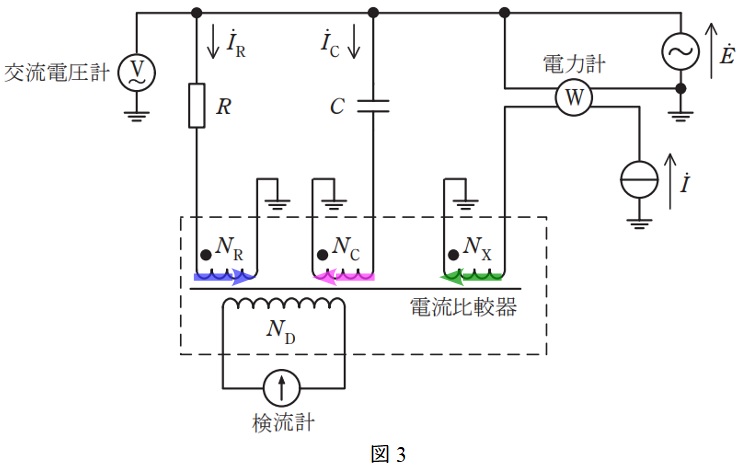
(3)解答：ニ
図3の通り，鉄心内の電流の流れる向きは\( \ {\dot I}_{\mathrm {R}} \ \)が右向き，\( \ {\dot I}_{\mathrm {C}} \ \)と\( \ \dot I \ \)が左向きなので，鉄心内の磁束が零になることから，ワンポイント解説「1.起磁力」の通り，
\[
\begin{eqnarray}
N_{\mathrm {R}}{\dot I}_{\mathrm {R}}-N_{\mathrm {C}}{\dot I}_{\mathrm {C}}-N_{\mathrm {X}}\dot I&=&0 \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ヌ
(5)解答：リ
(3)解答式を\( \ \dot I \ \)について整理すると，
\[
\begin{eqnarray}
N_{\mathrm {R}}{\dot I}_{\mathrm {R}}-N_{\mathrm {C}}{\dot I}_{\mathrm {C}}-N_{\mathrm {X}}\dot I&=&0 \\[ 5pt ] N_{\mathrm {X}}\dot I&=&N_{\mathrm {R}}{\dot I}_{\mathrm {R}}-N_{\mathrm {C}}{\dot I}_{\mathrm {C}} \\[ 5pt ] \dot I&=&\frac {N_{\mathrm {R}}{\dot I}_{\mathrm {R}}-N_{\mathrm {C}}{\dot I}_{\mathrm {C}}}{N_{\mathrm {X}}} \\[ 5pt ] \end{eqnarray}
\] となり，これに(1)，(2)解答式を代入すると，
\[
\begin{eqnarray}
\dot I&=&\frac {N_{\mathrm {R}}{\dot I}_{\mathrm {R}}-N_{\mathrm {C}}{\dot I}_{\mathrm {C}}}{N_{\mathrm {X}}} \\[ 5pt ] &=&\frac {\displaystyle N_{\mathrm {R}}\cdot \frac {\dot E}{R}-N_{\mathrm {C}}\cdot \mathrm {j}\omega C \dot E}{N_{\mathrm {X}}} \\[ 5pt ] &=&\frac {N_{\mathrm {R}}}{N_{\mathrm {X}}R}\dot E-\mathrm {j}\frac {N_{\mathrm {C}}\omega C}{N_{\mathrm {X}}}\dot E \\[ 5pt ] \end{eqnarray}
\] となるので，両辺に\( \ \dot E \ \)の共役複素数\( \ \overline E \ \)を乗じると，
\[
\begin{eqnarray}
\overline E\dot I&=&\frac {N_{\mathrm {R}}}{N_{\mathrm {X}}R}\left| \dot E\right| ^{2}-\mathrm {j}\frac {N_{\mathrm {C}}\omega C}{N_{\mathrm {X}}}\left| \dot E\right| ^{2} \\[ 5pt ] \end{eqnarray}
\] と求められる。