Contents
【問題】
【難易度】★★★★★(難しい)
次の文章は,同軸円筒導体間の電界に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
図1のように,内部導体の外半径を\( \ a \ \),外部導体の内半径を\( \ b \ \)とする同軸円筒導体を想定する。外部導体を接地し,内部導体に電圧\( \ V \ \)を印加するとき,内部導体に蓄えられる単位長さ当たりの電荷を\( \ Q \ \)とする。
内外導体間の誘電体の誘電率が\( \ \varepsilon _{1} \ \)の場合,半径\( \ r \ \)における電界\( \ E\left( r \right) \ \)は①式のように表される。
\[
\begin{eqnarray}
E\left( r \right) &=& \ \fbox { (1) } \ ・・・・・・・・・・・・・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
このときの\( \ E\left( r \right) \ \)の最小値を\( \ E_{\mathrm {min}} \ \),最大値を\( \ E_{\mathrm {max}} \ \)とする。なお,\( \ E\left( r \right) \ \)を\( \ r \ \)について\( \ a \ \)から\( \ b \ \)まで積分した値が内外円筒間の電位差\( \ V \ \)に等しいことから,この同軸円筒導体の単位長さ当たりの静電容量\( \ C \ \)は②式のようになる。
\[
\begin{eqnarray}
C&=& \ \fbox { (2) } \ \ \ ・・・・・・・・・・・・・・・・・・・・・・ ② \\[ 5pt ]
\end{eqnarray}
\]
次に,図2のように内外導体間の誘電体の誘電率が\( \ r \ \)の一次関数\( \ \varepsilon \left( r \right) \ \)として\( \ \varepsilon \left( a \right) =\varepsilon _{2} \ \)から\( \ \varepsilon \left( b \right) =\varepsilon _{1} \ \)まで変化する同軸円筒導体を考える。この場合,\( \ \varepsilon \left( r \right) \ \)は③式のように表される。
\[
\begin{eqnarray}
\varepsilon \left( r \right) &=&\frac {\varepsilon _{1}-\varepsilon _{2}}{b-a}r+ \ \fbox { (3) } \ ・・・・・・・・・・・・・・・ ③ \\[ 5pt ]
\end{eqnarray}
\]
この場合に,内部導体に図1と同じ電荷\( \ Q \ \)を与える場合の内外導体間の電界を\( \ E_{1}\left( r \right) \ \)と表記する。①式で\( \ E_{\mathrm {max}} \ \)となる\( \ r=r_{\mathrm {max}} \ \)において,\( \ E_{1}\left( r_{\mathrm {max}} \right) ≦E_{\mathrm {min}} \ \)となるための\( \ \varepsilon _{2} \ \)の条件は,①式の\( \ \varepsilon _{1} \ \)を\( \ \varepsilon \left( r \right) \ \)に置き換えることにより,\( \ \varepsilon _{2}≧ \ \fbox { (4) } \ \)と算出される。\( \ \varepsilon _{2}= \ \fbox { (4) } \ \)のとき,\( \ E_{1}\left( r \right) \ \)は\( \ r= \ \fbox { (5) } \ \)において最小となる。
〔問1の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {\varepsilon _{2}b-\varepsilon _{1}a}{b-a} &(ロ)& \varepsilon _{1}-\varepsilon _{2} &(ハ)& \frac {\varepsilon _{1}b-\varepsilon _{2}a}{b-a} \\[ 5pt ]
&(ニ)& \frac {2\pi \varepsilon _{1}}{\displaystyle \ln \frac {b}{a}} &(ホ)& \frac {a+b}{2} &(ヘ)& \frac {Q}{4\pi r\varepsilon _{1}} \\[ 5pt ]
&(ト)& \frac {a}{b}\varepsilon _{1} &(チ)& \frac {Q}{2\pi r\varepsilon _{1}} &(リ)& \frac {Q}{2\pi r^{2}\varepsilon _{1}} \\[ 5pt ]
&(ヌ)& \frac {2\pi \varepsilon _{1}}{b-a} &(ル)& \frac {2\pi \varepsilon _{1}}{\displaystyle \ln \frac {a}{b}} &(ヲ)& b \\[ 5pt ]
&(ワ)& \varepsilon _{1} &(カ)& \frac {b}{a}\varepsilon _{1} &(ヨ)& a \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
同軸円筒導体間の電界に関する問題です。
(4)以降の計算量が多く,問題文もわかりにくいため,かなり受験生は苦戦したと考えられます。
(3)までできたら,とりあえずは合格圏内と考えると良いかと思います。
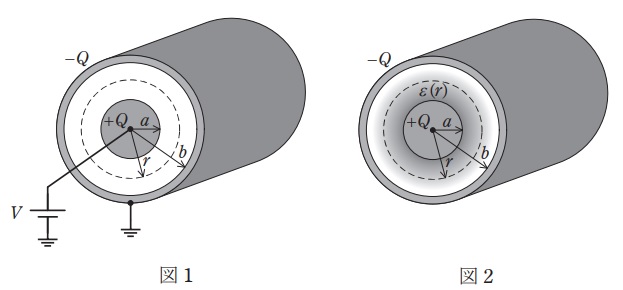
1.ガウスの法則
\( \ Q \ \mathrm {[C]} \ \)から出る電気力線は\( \ \displaystyle \frac {Q}{\varepsilon } \ \)本,電束は\( \ Q \ \)本であり,電界\( \ E \ \mathrm {[V / m]} \ \)及び電束密度\( \ D \ \mathrm {[C / m^{2}]} \ \)との関係は,任意の閉曲面において,
\[
\begin{eqnarray}
\int _{S} \boldsymbol E \cdot \mathrm {d}\boldsymbol S &=& \frac {Q}{\varepsilon } \\[ 5pt ]
\int _{S} \boldsymbol D \cdot \mathrm {d}\boldsymbol S &=& Q \\[ 5pt ]
\end{eqnarray}
\]
となり,これをガウスの法則といいます。閉曲面が球で,点電荷に蓄えられている電荷\( \ Q \ \mathrm {[C]} \ \)があれば,電界\( \ E \ \mathrm {[V / m]} \ \)は,
\[
\begin{eqnarray}
4\pi r^{2} \cdot E &=& \frac {Q}{\varepsilon } \\[ 5pt ]
E &=& \frac {Q}{4\pi \varepsilon r^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
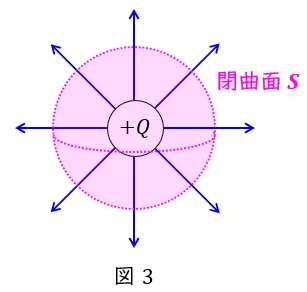
2.空間上の電位\( \ V \ \)
中心からの距離\( \ r \ \mathrm {[m]} \ \)に関する電界\( \ E_{\mathrm {r}} \ \mathrm {[V / m]} \ \)が与えられている時,その場所の電位\( \ V \ \mathrm {[V]} \ \)は無限遠を基準とすると,
\[
\begin{eqnarray}
V&=&-\int _{\infty }^{r}E_{\mathrm {r}}\mathrm {d}r \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
【解答】
(1)解答:チ
単位長さあたりの電荷が\( \ Q \ \)であるから,ワンポイント解説「1.ガウスの法則」より,
\[
\begin{eqnarray}
2\pi r\times 1\times E\left( r \right) &=& \frac {Q}{\varepsilon _{1}} \\[ 5pt ]
E\left( r \right) &=& \frac {Q}{2\pi r\varepsilon _{1}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ニ
(1)解答式より,内外円筒間の電位差\( \ V \ \)は,ワンポイント解説「2.空間上の電位\( \ V \ \)」の通り,
\[
\begin{eqnarray}
V&=&-\int _{b}^{a}E\left( r \right) \mathrm {d}r \\[ 5pt ]
&=&-\int _{b}^{a}\frac {Q}{2\pi r\varepsilon _{1}}\mathrm {d}r \\[ 5pt ]
&=&\int _{a}^{b}\frac {Q}{2\pi r\varepsilon _{1}}\mathrm {d}r \\[ 5pt ]
&=&\frac {Q}{2\pi \varepsilon _{1}}\int _{a}^{b}\frac {1}{r}\mathrm {d}r \\[ 5pt ]
&=&\frac {Q}{2\pi \varepsilon _{1}}\left[ \ln r\right] _{a}^{b} \\[ 5pt ]
&=&\frac {Q}{2\pi \varepsilon _{1}}\left( \ln b-\ln a\right) \\[ 5pt ]
&=&\frac {Q}{2\pi \varepsilon _{1}}\ln \frac {b}{a} \\[ 5pt ]
\end{eqnarray}
\]
となるので,静電容量\( \ C \ \)は,
\[
\begin{eqnarray}
C &=& \frac {Q}{V} \\[ 5pt ]
&=& \frac {Q}{\displaystyle \frac {Q}{2\pi \varepsilon _{1}}\ln \frac {b}{a}} \\[ 5pt ]
&=& \frac {1}{\displaystyle \frac {1}{2\pi \varepsilon _{1}}\ln \frac {b}{a}} \\[ 5pt ]
&=& \frac {2\pi \varepsilon _{1}}{\displaystyle \ln \frac {b}{a}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:イ
誘電体の誘電率が\( \ r \ \)の一次関数なので,\( \ \varepsilon \left( r \right) =Ar+B \ \)とおく。\( \ \varepsilon \left( a \right) =\varepsilon _{2} \ \)及び\( \ \varepsilon \left( b \right) =\varepsilon _{1} \ \)であるから,
\[
\begin{eqnarray}
\left\{
\begin{array}{l}
\varepsilon _{2} &=&Aa+B &・・・・・・・・・ ④& \\[ 5pt ]
\varepsilon _{1} &=&Ab+B &・・・・・・・・・ ⑤& \\[ 5pt ]
\end{array}
\right.
\end{eqnarray}
\]
となる。\( \ ⑤-④ \ \)より,
\[
\begin{eqnarray}
\varepsilon _{1}-\varepsilon _{2} &=&Ab-Aa \\[ 5pt ]
&=&A\left( b-a \right) \\[ 5pt ]
A&=&\frac {\varepsilon _{1}-\varepsilon _{2}}{b-a} \\[ 5pt ]
\end{eqnarray}
\]
となり,これを④式に代入すると,
\[
\begin{eqnarray}
\varepsilon _{2} &=&\frac {\varepsilon _{1}-\varepsilon _{2}}{b-a}\cdot a+B \\[ 5pt ]
B &=&\varepsilon _{2} -\frac {\varepsilon _{1}-\varepsilon _{2}}{b-a}\cdot a \\[ 5pt ]
&=&\frac {\varepsilon _{2}\left( b-a\right) }{b-a} -\frac {\left(\varepsilon _{1}-\varepsilon _{2}\right) a}{b-a} \\[ 5pt ]
&=&\frac {\varepsilon _{2}b-\varepsilon _{2}a-\varepsilon _{1}a+\varepsilon _{2}a }{b-a} \\[ 5pt ]
&=&\frac {\varepsilon _{2}b-\varepsilon _{1}a}{b-a} \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
\varepsilon \left( r \right) &=&\frac {\varepsilon _{1}-\varepsilon _{2}}{b-a}r+\frac {\varepsilon _{2}b-\varepsilon _{1}a}{b-a} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:カ
①式で\( \ E_{\mathrm {max}} \ \)及び\( \ E_{\mathrm {min}} \ \)となる\( \ r=r_{\mathrm {max}} \ \)及び\( \ r=r_{\mathrm {min}} \ \)は,
\[
\begin{eqnarray}
r_{\mathrm {max}} &=&a \\[ 5pt ]
r_{\mathrm {min}} &=&b \\[ 5pt ]
\end{eqnarray}
\]
であり,(1)解答式より,\( \ E_{\mathrm {min}} \ \)は,
\[
\begin{eqnarray}
E_{\mathrm {min}} &=& \frac {Q}{2\pi b\varepsilon _{1}}\\[ 5pt ]
\end{eqnarray}
\]
である。次に,(1)解答式の\( \ \varepsilon _{1} \ \)に\( \ \displaystyle \varepsilon \left( r \right) =\frac {\varepsilon _{1}-\varepsilon _{2}}{b-a}r+\frac {\varepsilon _{2}b-\varepsilon _{1}a}{b-a} \ \)と代入すると,
\[
\begin{eqnarray}
E_{1}\left( r \right) &=& \frac {Q}{2\pi r\varepsilon \left( r \right) } \\[ 5pt ]
&=& \frac {Q}{\displaystyle 2\pi r \left( \frac {\varepsilon _{1}-\varepsilon _{2}}{b-a}r+\frac {\varepsilon _{2}b-\varepsilon _{1}a}{b-a} \right) } \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ E_{1}\left( r_{\mathrm {max}} \right) \ \)は,
\[
\begin{eqnarray}
E_{1}\left( r_{\mathrm {max}} \right) &=& \frac {Q}{\displaystyle 2\pi a \left( \frac {\varepsilon _{1}-\varepsilon _{2}}{b-a}a+\frac {\varepsilon _{2}b-\varepsilon _{1}a}{b-a} \right) } \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,\( \ E_{1}\left( r_{\mathrm {max}} \right) ≦E_{\mathrm {min}} \ \)となるための\( \ \varepsilon _{2} \ \)の条件は,
\[
\begin{eqnarray}
\frac {Q}{\displaystyle 2\pi a \left( \frac {\varepsilon _{1}-\varepsilon _{2}}{b-a}a+\frac {\varepsilon _{2}b-\varepsilon _{1}a}{b-a} \right) }&≦&\frac {Q}{2\pi b\varepsilon _{1}} \\[ 5pt ]
\frac {1}{\displaystyle a \left( \frac {\varepsilon _{1}-\varepsilon _{2}}{b-a}a+\frac {\varepsilon _{2}b-\varepsilon _{1}a}{b-a} \right) }&≦&\frac {1}{ b\varepsilon _{1}} \\[ 5pt ]
a \left( \frac {\varepsilon _{1}-\varepsilon _{2}}{b-a}a+\frac {\varepsilon _{2}b-\varepsilon _{1}a}{b-a} \right) &≧&b\varepsilon _{1} \\[ 5pt ]
a \cdot \frac {\varepsilon _{1}a-\varepsilon _{2}a+\varepsilon _{2}b-\varepsilon _{1}a}{b-a}&≧&b\varepsilon _{1} \\[ 5pt ]
a \cdot \frac {-\varepsilon _{2}a+\varepsilon _{2}b}{b-a}&≧&b\varepsilon _{1} \\[ 5pt ]
a \cdot \frac {\varepsilon _{2}\left( b-a\right) }{b-a}&≧&b\varepsilon _{1} \\[ 5pt ]
a \varepsilon _{2}&≧&b\varepsilon _{1} \\[ 5pt ]
\varepsilon _{2}&≧&\frac {b}{a}\varepsilon _{1} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ホ
\( \ \displaystyle \varepsilon _{2}=\frac {b}{a}\varepsilon _{1} \ \)のとき,\( \ E_{1}\left( r \right) \ \)は,
\[
\begin{eqnarray}
E_{1}\left( r \right) &=& \frac {Q}{\displaystyle 2\pi r \left( \frac {\displaystyle \varepsilon _{1}-\frac {b}{a}\cdot \varepsilon _{1}}{b-a}r+\frac {\displaystyle \frac {b}{a}\varepsilon _{1}\cdot b-\varepsilon _{1}a}{b-a} \right) } \\[ 5pt ]
&=& \frac {Q}{\displaystyle 2\pi r \left\{ \frac {\displaystyle a\varepsilon _{1}-b \varepsilon _{1}}{a\left( b-a\right) }r+\frac {\displaystyle b^{2}\varepsilon _{1}-a^{2}\varepsilon _{1}}{a\left( b-a\right) } \right\} } \\[ 5pt ]
&=& \frac {Q}{\displaystyle 2\pi r \left\{ \frac {\displaystyle \left( a-b\right) \varepsilon _{1}}{a\left( b-a\right) }r+\frac {\displaystyle \left(b+a \right) \left(b-a \right) \varepsilon _{1}}{a\left( b-a\right) } \right\} } \\[ 5pt ]
&=& \frac {Q}{\displaystyle 2\pi r \left\{ -\frac { \varepsilon _{1}}{a}r+\frac {\displaystyle \left(b+a \right) \varepsilon _{1}}{a} \right\} } \\[ 5pt ]
&=& \frac {Q}{\displaystyle \frac {2\pi \varepsilon _{1}}{a}r \left\{ -r+\left(b+a \right)\right\} } \\[ 5pt ]
&=& \frac {Q}{\displaystyle \frac {2\pi \varepsilon _{1}}{a} \left\{ -r^{2}+\left(a+b \right)r\right\} } \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ f\left( r \right) = -r^{2}+\left(a+b \right)r \ \)とすると,\( \ f\left( r \right) \ \)が最大となるとき\( \ E_{1}\left( r \right) \ \)が最小となる。したがって,このときの\( \ r \ \)は,
\[
\begin{eqnarray}
\frac {\mathrm {d}f\left( r \right) }{\mathrm {d}r} =-2r+\left(a+b \right) &=&0 \\[ 5pt ]
2r&=&a+b \\[ 5pt ]
r&=&\frac {a+b}{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは