Contents
【問題】
【難易度】★★★★☆(やや難しい)
原子力発電に用いられる\( \ 5.0 \ \mathrm {[g]} \ \)のウラン\( \ 235 \ \)を核分裂させたときに発生するエネルギーを考える。ここで想定する原子力発電所では,上記エネルギーの\( \ 30 \ \mathrm {[%]} \ \)を電力量として取り出すことができるものとする。これを用いて,揚程\( \ 200 \ \mathrm {[m]} \ \),揚水時の総合的効率を\( \ 84 \ \mathrm {[%]} \ \)としたとき,揚水発電所で揚水できる水量\( \ \mathrm {[m^{3}]} \ \)の値として,最も近いのは次のうちどれか。
ただし,ここでは原子力発電所から揚水発電所への送電で生じる損失は無視できるものとする。
なお,計算には必要に応じて次の数値を用いること。
核分裂時のウラン\( \ 235 \ \)の質量欠損\( \ 0.09 \ \mathrm {[%]} \ \)
ウランの原子番号\( \ 92 \ \)
真空中の光の速度\( \ c=3.0\times 10^{8} \ \mathrm {[m / s]} \ \)
\( (1) \) \( \ 2.6\times 10^{4} \ \) \( (2) \) \( \ 4.2\times 10^{4} \ \) \( (3) \) \( \ 5.2\times 10^{4} \ \)
\( (4) \) \( \ 6.1\times 10^{4} \ \) \( (5) \) \( \ 9.7\times 10^{4} \ \)
【ワンポイント解説】
原子力発電で発生するエネルギーと揚水量の関係を関係を考える問題です。
単位の変換等を駆使して解くやや難易度が高い問題です。
\( \ 10 \ \ \)の累乗の計算が最初なかなか合わないかもしれませんが,一つずつよく考えて理解していくようにして下さい。
1.エネルギーと質量の関係式
アインシュタインの特殊相対性理論の中でも最もポピュラーな公式の一つで,ある物質に\( \ \Delta m \ \mathrm {[kg]} \ \)の質量欠損があった場合,その物質から発生するエネルギーを\( \ E \ \mathrm {[J]} \ \),光の速度を\( \ c=3.0\times 10^{8} \ \mathrm {[m / s]} \ \)とすると,
\[
\begin{eqnarray}
E &=&\Delta m c^{2} \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。
2.\( \ \mathrm {[kJ]} \ \)と\( \ \mathrm {[kW\cdot h]} \ \)の変換
単位の定義より,
\[
\begin{eqnarray}
1 \ \mathrm {[kJ / s]} &=&1 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
であるから,両辺の単位に\( \ \mathrm {[s]} \ \)をかけると,
\[
\begin{eqnarray}
1 \ \mathrm {[kJ]} &=&1 \ \mathrm {[kW\cdot s]} \\[ 5pt ]
\end{eqnarray}
\]
となり,両辺に\( \ 1 \ \mathrm {[h]}=3 \ 600 \ \mathrm {[s]} \ \)を考慮して,\( \ 3 \ 600 \ \)をかけると,
\[
\begin{eqnarray}
3 \ 600 \ \mathrm {[kJ]} &=&1 \ \mathrm {[kW\cdot h]} \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.揚水発電所の諸公式
揚水発電で使用される諸公式は以下の通りです。本問で使用しない公式も覚えておくようにしましょう。
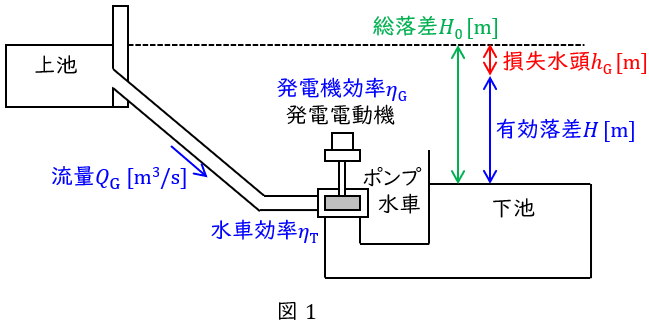
①発電電力
有効落差 :\( \ H=H_{0}-h_{\mathrm {G}} \ \mathrm {[ m ] } \ \)
発電機出力:\( \ P_{\mathrm {G}}=9.8Q_{\mathrm {G}}H\eta _{\mathrm {T}}\eta _{\mathrm {G}} \ \mathrm {[ kW ] } \ \)
総発電量 :\( \ W_{\mathrm {G}}=P_{\mathrm {G}}T_{\mathrm {G}} \ \mathrm {[ kW\cdot h ] } \ \)
ただし,\( \ H_{0} \ \)は総落差\( \ \mathrm {[m]} \ \),\( \ h_{\mathrm {G}} \ \)は発電時の損失水頭\( \ \mathrm {[m]} \ \),\( \ Q_{\mathrm {G}} \ \)は発電時の流量\( \ \mathrm {[m^{3} / s]} \ \),\( \ \eta _{\mathrm {T}} \ \)は水車効率,\( \ \eta _{\mathrm {G}} \ \)は発電機効率,\( \ T_{\mathrm {G}} \ \)は発電時間\( \ \mathrm {[h]} \ \)
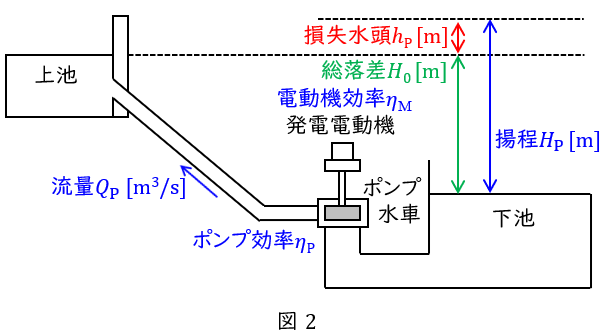
②揚水動力
必要揚程 :\( \ \displaystyle H_{\mathrm {P}}=H_{0}+h_{\mathrm {P}} \ \mathrm {[ m ] } \ \)
所要動力 :\( \ \displaystyle P_{\mathrm {M}}=\frac { 9.8Q_{\mathrm {P}}H_{\mathrm {P}}}{\eta _{\mathrm {P}}\eta _{\mathrm {M}} } \ \mathrm {[ kW ] } \ \)
所要電力量:\( \ W_{\mathrm {M}}=P_{\mathrm {M}}T_{\mathrm {M}} \ \mathrm {[ kW\cdot h ] } \ \)
ただし,\( \ H_{0} \ \)は総落差\( \ \mathrm {[m]} \ \),\( \ h_{\mathrm {P}} \ \)は揚水時の損失水頭\( \ \mathrm {[m]} \ \),\( \ Q_{\mathrm {P}} \ \)は揚水時の流量\( \ \mathrm {[m^{3} / s]} \ \),\( \ \eta _{\mathrm {P}} \ \)はポンプ効率,\( \ \eta _{\mathrm {M}} \ \)は電動機効率,\( \ T_{\mathrm {M}} \ \)は揚水時間\( \ \mathrm {[h]} \ \)
③揚水総合効率
\[
\begin{eqnarray}
\eta &=&\frac {W_{\mathrm {G}}}{W_{\mathrm {M}}} \\[ 5pt ]
&=&\frac {9.8Q_{\mathrm {G}}H\eta _{\mathrm {T}}\eta _{\mathrm {G}}T_{\mathrm {G}}}{\displaystyle \frac { 9.8Q_{\mathrm {P}}H_{\mathrm {P}}}{\eta _{\mathrm {P}}\eta _{\mathrm {M}} }T_{\mathrm {M}}} \\[ 5pt ]
&=&\frac {Q_{\mathrm {G}}HT_{\mathrm {G}}}{Q_{\mathrm {P}}H_{\mathrm {P}}T_{\mathrm {M}}}\eta _{\mathrm {T}}\eta _{\mathrm {G}}\eta _{\mathrm {P}}\eta _{\mathrm {M}} \\[ 5pt ]
&=&\frac {H}{H_{\mathrm {P}}}\eta _{\mathrm {T}}\eta _{\mathrm {G}}\eta _{\mathrm {P}}\eta _{\mathrm {M}} \left( ∵ Q_{\mathrm {G}}T_{\mathrm {G}}\times 3 \ 600=Q_{\mathrm {P}}T_{\mathrm {M}}\times 3 \ 600\right) \\[ 5pt ]
\end{eqnarray}
\]
【解答】
解答:(3)
\( \ m=5.0\times 10^{-3} \ \mathrm {[kg]} \ \)のウラン\( \ 235 \ \)を核分裂させたときに発生するエネルギー\( \ E \ \mathrm {[kJ]} \ \)は,ワンポイント解説「1.エネルギーと質量の関係式」の通り,
\[
\begin{eqnarray}
E &=&\frac {0.09}{100}mc^{2} \\[ 5pt ]
&=&\frac {0.09}{100}\times 5.0\times 10^{-3}\times \left( 3.0 \times 10^{8}\right) ^{2} \\[ 5pt ]
&=&4.05\times 10^{11} \ \mathrm {[J]} → 4.05\times 10^{8} \ \mathrm {[kJ]} \\[ 5pt ]
\end{eqnarray}
\]
となり,このうち取り出せる電力量は\( \ 30 \ \mathrm {[%]} \ \)なので,取り出せる電力量\( \ W \ \mathrm {[kW\cdot h]} \ \)は,ワンポイント解説「2.\( \ \mathrm {[kJ]} \ \)と\( \ \mathrm {[kW\cdot h]} \ \)の変換」の通り,
\[
\begin{eqnarray}
W &=&\frac {0.30E}{3 \ 600} \\[ 5pt ]
&=&\frac {0.30\times 4.05\times 10^{8}}{3 \ 600} \\[ 5pt ]
&=&3.375\times 10^{4} \ \mathrm {[kW\cdot h]} \\[ 5pt ]
\end{eqnarray}
\]
となる。一方,揚水発電所において,揚程\( \ H_{\mathrm {P}}=200 \ \mathrm {[m]} \ \),揚水時の総合的効率\( \ \eta =84 \ \mathrm {[%]} \ \),流量\( \ Q_{\mathrm {P}} \ \mathrm {[m^{3}/s]} \ \)とすると,動力\( \ P_{\mathrm {M}} \ \mathrm {[ kW ] } \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {M}} &=&\frac { 9.8Q_{\mathrm {P}}H_{\mathrm {P}}}{\eta} \\[ 5pt ]
&=&\frac { 9.8Q_{\mathrm {P}}\times 200}{0.84} \\[ 5pt ]
&≒&2 \ 333Q_{\mathrm {P}} \\[ 5pt ]
\end{eqnarray}
\]
となり,揚水量を\( \ V \ \mathrm {[m^{3}]} \ \),揚水時間を\( \ T \ \mathrm {[h]} \ \)とすれば,
\[
\begin{eqnarray}
V&=&3 \ 600Q_{\mathrm {P}}T \\[ 5pt ]
Q_{\mathrm {P}}&=&\frac { V}{3 \ 600T} \\[ 5pt ]
\end{eqnarray}
\]
の関係があるから,
\[
\begin{eqnarray}
P_{\mathrm {M}} &=&2 \ 333Q_{\mathrm {P}} \\[ 5pt ]
&=&2 \ 333\times \frac { V}{3 \ 600T} \\[ 5pt ]
&=& \frac {0.648 \ 06 V}{T} \\[ 5pt ]
\end{eqnarray}
\]
となる。本問においては取り出せる電力をすべて揚水したと考えれば良いので,
\[
\begin{eqnarray}
W &=&P_{\mathrm {M}}T \\[ 5pt ]
3.375\times 10^{4}&=&\frac {0.648 \ 06 V}{T}\times T \\[ 5pt ]
&=&0.648 \ 06 V \\[ 5pt ]
V&≒&5.2\times 10^{4} \ \mathrm {[m^{3}]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは