【問題】
【難易度】★★★★☆(やや難しい)
図に示すように,中性点をリアクトル\(\mathrm {L}\)を介して接地している公称電圧\(66 \ \mathrm {kV}\)の系統があるとき,次の(a)及び(b)の問に答えよ。なお,図中の\(\mathrm {C}\)は,送電線の対地静電容量に相当する等価キャパシタを示す。また,図に表示されていない電気定数は無視する。
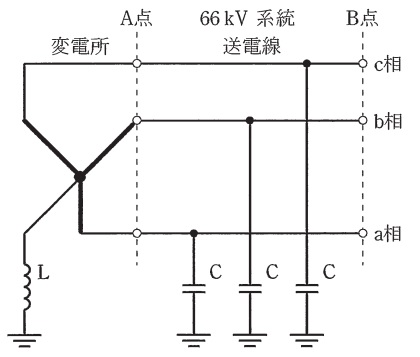
(a) 送電線の線路定数を測定するために,図中の\(\mathrm {A}\)点で変電所と送電線を切り離し,\(\mathrm {A}\)点での送電線の3線を一括して,これと大地間に公称電圧の相電圧相当の電圧を加えて充電すると,一括した線に流れる全充電電流は\(115 \ \mathrm {A}\)であった。このとき,この送電線の1相当たりのアドミタンスの大きさ\(\mathrm {[mS]}\)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 0.58 (2) 1.0 (3) 1.7 (4) 3.0 (5) 9.1
(b) 図中の\(\mathrm {B}\)点の\(\mathrm {a}\)相で1線地絡事故が発生したとき,地絡点を流れる電流を零とするために必要なリアクトル\(\mathrm {L}\)のインピーダンスの大きさ\(\mathrm {[\Omega ]}\)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし,送電線の電気定数は,(a)で求めた値を用いるものとする。
(1) 111 (2) 196 (3) 333 (4) 575 (5) 1000
【ワンポイント解説】
(b)の地絡点に流れる電流を零というのは,共振の条件と同義となります。(a)を間違えると(b)も間違えてしまうため,計算間違いをしないようにしましょう。
【関連する「電気の神髄」記事】
【解答】
(a)解答:(2)
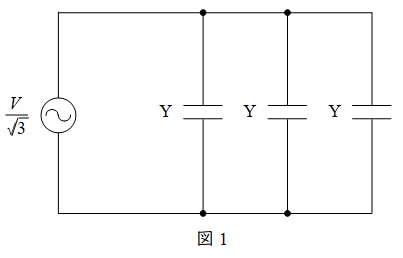
公称電圧の相電圧相当の電圧を加えた時の等価回路は図1のようになる。
この回路に流れる電流\(I=115 \ \mathrm {A}\)であり,合成アドミタンスの大きさが\(3Y\)であるから,
\[
\begin{eqnarray}
I&=&3Y\frac {V}{\sqrt {3}} \\[ 5pt ]
Y&=&\frac {I}{\sqrt {3}V} \\[ 5pt ]
&=&\frac {115}{\sqrt {3}\times 66\times 10^{3}} \\[ 5pt ]
&≒&0.0010 \ \mathrm {[S]} → 1.0 \ \mathrm {[mS]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(b)解答:(3)
1線地絡事故時に地絡点に流れる電流を零とするためには,リアクトルとコンデンサの合成インピーダンスが零となるように調整すれば,地絡点には電流が流れなくなる。
よって,リアクトルのインピーダンスを\(X_{\mathrm {L}}\)とすると,
\[
\begin{eqnarray}
X_{\mathrm {L}}&=&\frac {1}{3Y} \\[ 5pt ]
&=&\frac {1}{3\times 0.0010} \\[ 5pt ]
&≒&333 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは