《電力》〈水力〉[R06上:問2]揚水発電所の電動機入力と発電機出力に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

総落差\( \ 200 \ \mathrm {m} \ \)，ポンプ水車・発電電動機\( \ 1 \ \)台よりなる揚水発電所がある。揚水時･発電時共に流量は\( \ 100 \ \mathrm {m^{3} / s} \ \)，損失水頭は揚水･発電共に総落差の\( \ 2.5 \ \mathrm {％} \ \)，ポンプ効率･水車効率共に\( \ 85 \ \mathrm {％} \ \)，発電効率･電動機効率共に\( \ 98 \ \mathrm {％} \ \)とし，損失水頭及び上記\( \ 4 \ \)種の効率は，揚程，落差，出力，入力の変化によらず一定とする。

揚水時の電動機入力\( \ \mathrm {[MW]} \ \)と，発電時の発電機出力\( \ \mathrm {[MW]} \ \)の組合せとして，最も近いものを次の(1)～(5)のうちから一つ選べ。

\[
\begin{array}{ccc}
& 　電動機入力 \ \mathrm {[MW]}　 & 　発電機出力 \ \mathrm {[MW]}　 \\
\hline
(1) & 　235　 & 　163　 \\
\hline
(2) & 　235　 & 　159　 \\
\hline
(3) & 　241　 & 　163　 \\
\hline
(4) & 　241　 & 　159　 \\
\hline
(5) & 　229　 & 　167　 \\
\hline
\end{array}
\]

【ワンポイント解説】

揚水発電所の電動機入力及び発電機出力を求める問題です。
使用する公式はいずれも揚水発電の基本公式となりますので，練習問題としてもとても良い問題です。
計算間違いに注意して確実に解けるようになりましょう。
平成28年問1に類題も出題されていますので，合わせて見ておいて下さい。

1.揚水発電所の諸公式
揚水発電で使用される諸公式は以下の通りです。本問で使用しない公式も覚えておくようにしましょう。

①発電電力
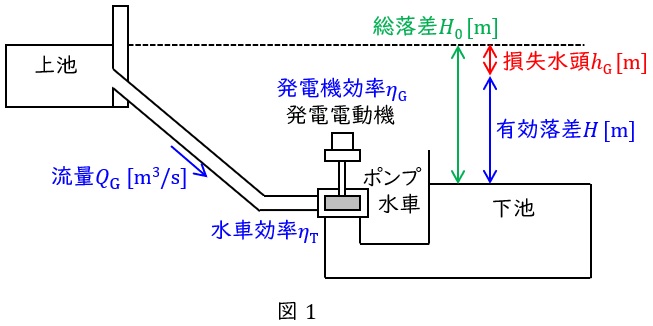
有効落差　：\( \ H=H_{0}-h_{\mathrm {G}} \ \mathrm {[ m ] } \ \)
発電機出力：\( \ P_{\mathrm {G}}=9.8Q_{\mathrm {G}}H\eta _{\mathrm {T}}\eta _{\mathrm {G}} \ \mathrm {[ kW ] } \ \)
総発電量　：\( \ W_{\mathrm {G}}=P_{\mathrm {G}}T_{\mathrm {G}} \ \mathrm {[ kW\cdot h ] } \ \)

ただし，\( \ H_{0} \ \)は総落差\( \ \mathrm {[m]} \ \)，\( \ h_{\mathrm {G}} \ \)は発電時の損失水頭\( \ \mathrm {[m]} \ \)，\( \ Q_{\mathrm {G}} \ \)は発電時の流量\( \ \mathrm {[m^{3} / s]} \ \)，\( \ \eta _{\mathrm {T}} \ \)は水車効率，\( \ \eta _{\mathrm {G}} \ \)は発電機効率，\( \ T_{\mathrm {G}} \ \)は発電時間\( \ \mathrm {[h]} \ \)

②揚水動力
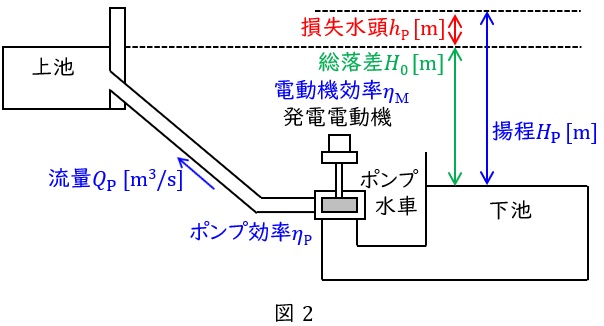
必要揚程　：\( \ \displaystyle H_{\mathrm {P}}=H_{0}+h_{\mathrm {P}} \ \mathrm {[ m ] } \ \)
所要動力　：\( \ \displaystyle P_{\mathrm {M}}=\frac { 9.8Q_{\mathrm {P}}H_{\mathrm {P}}}{\eta _{\mathrm {P}}\eta _{\mathrm {M}} } \ \mathrm {[ kW ] } \ \)
所要電力量：\( \ W_{\mathrm {M}}=P_{\mathrm {M}}T_{\mathrm {M}} \ \mathrm {[ kW\cdot h ] } \ \)

ただし，\( \ H_{0} \ \)は総落差\( \ \mathrm {[m]} \ \)，\( \ h_{\mathrm {P}} \ \)は揚水時の損失水頭\( \ \mathrm {[m]} \ \)，\( \ Q_{\mathrm {P}} \ \)は揚水時の流量\( \ \mathrm {[m^{3} / s]} \ \)，\( \ \eta _{\mathrm {P}} \ \)はポンプ効率，\( \ \eta _{\mathrm {M}} \ \)は電動機効率，\( \ T_{\mathrm {M}} \ \)は揚水時間\( \ \mathrm {[h]} \ \)

③揚水総合効率
\[
\begin{eqnarray}
\eta &=&\frac {W_{\mathrm {G}}}{W_{\mathrm {M}}} \\[ 5pt ] &=&\frac {9.8Q_{\mathrm {G}}H\eta _{\mathrm {T}}\eta _{\mathrm {G}}T_{\mathrm {G}}}{\displaystyle \frac { 9.8Q_{\mathrm {P}}H_{\mathrm {P}}}{\eta _{\mathrm {P}}\eta _{\mathrm {M}} }T_{\mathrm {M}}} \\[ 5pt ] &=&\frac {Q_{\mathrm {G}}HT_{\mathrm {G}}}{Q_{\mathrm {P}}H_{\mathrm {P}}T_{\mathrm {M}}}\eta _{\mathrm {T}}\eta _{\mathrm {G}}\eta _{\mathrm {P}}\eta _{\mathrm {M}} \\[ 5pt ] &=&\frac {H}{H_{\mathrm {P}}}\eta _{\mathrm {T}}\eta _{\mathrm {G}}\eta _{\mathrm {P}}\eta _{\mathrm {M}}　\left( ∵ Q_{\mathrm {G}}T_{\mathrm {G}}\times 3 \ 600=Q_{\mathrm {P}}T_{\mathrm {M}}\times 3 \ 600\right) \\[ 5pt ] \end{eqnarray}
\]

【解答】

解答：(4)
①電動機入力
総落差\( \ H_{\mathrm {0}}=200 \ \mathrm {[m] } \ \)，損失水頭が\( \ 2.5 \ \mathrm {％} \ \)なので，必要揚程\( \ H_{\mathrm {P}} \ \mathrm {[m] } \ \)は，
\[
\begin{eqnarray}
H_{\mathrm {P}} &=&1.025\times 200 \\[ 5pt ] &=&205 \ \mathrm {[m] } \\[ 5pt ] \end{eqnarray}
\] となる。流量\( \ Q _{\mathrm {P}}=100 \ \mathrm {[m^{3} / s]} \ \)，ポンプ効率\( \ \eta _{\mathrm {P}}=0.85 \ \)，電動機効率\( \ \eta _{\mathrm {M}}=0.98 \ \)より，電動機入力\( \ P_{\mathrm {M}} \ \mathrm {[MW]} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {M}} &=&\frac { 9.8Q_{\mathrm {P}}H_{\mathrm {P}}}{\eta _{\mathrm {P}}\eta _{\mathrm {M}} } \\[ 5pt ] &=&\frac { 9.8\times 100\times 205}{0.85\times 0.98} \\[ 5pt ] &≒&241 \ 000 \ \mathrm {[kW]}　→　241 \ \mathrm {[MW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

②発電機出力
総落差\( \ H_{\mathrm {0}}=200 \ \mathrm {[m] } \ \)，損失水頭が\( \ 2.5 \ \mathrm {％} \ \)なので，有効落差\( \ H \ \mathrm {[m] } \ \)は，
\[
\begin{eqnarray}
H &=&0.975\times 200 \\[ 5pt ] &=&195 \ \mathrm {[m] } \\[ 5pt ] \end{eqnarray}
\] となる。流量\( \ Q _{\mathrm {G}}=100 \ \mathrm {[m^{3} / s]} \ \)，水車効率\( \ \eta _{\mathrm {T}}=0.85 \ \)，発電効率\( \ \eta _{\mathrm {G}}=0.98 \ \)より，発電機出力\( \ P_{\mathrm {G}} \ \mathrm {[MW]} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {G}} &=&9.8Q_{\mathrm {G}}H\eta _{\mathrm {T}}\eta _{\mathrm {G}} \\[ 5pt ] &=&9.8\times 100\times 195\times 0.85\times 0.98 \\[ 5pt ] &≒&159 \ 000 \ \mathrm {[kW]}　→　159 \ \mathrm {[MW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。