《電力》〈水力〉[H26:問15]ベルヌーイの定理を利用した計算に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

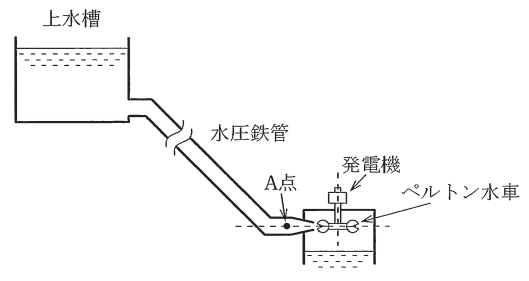
ペルトン水車を1台もつ水力発電所がある。図に示すように，水車の中心線上に位置する鉄管の\(\mathrm {A}\)点において圧力\(p \ \mathrm {[Pa]}\)と流速\(v \ \mathrm {[m / s ]}\)を測ったところ，それぞれ\(3000 \ \mathrm {kPa}\)，\(5.3 \ \mathrm {m / s }\)の値を得た。また，この\(\mathrm {A}\)点の鉄管断面は内径\(1.2 \ \mathrm {m}\)の円である。次の(a)及び(b)の問に答えよ。

ただし，\(\mathrm {A}\)点における全水頭\(H \ \mathrm {[m]}\)は位置水頭，圧力水頭，速度水頭の総和として\(\displaystyle h+\frac {p}{\rho g}+\frac {v^{2}}{2g}\)より計算できるが，位置水頭\(h\)は\(\mathrm {A}\)点が水車中心線上に位置することから無視できるものとする。また，重力加速度は\(g=9.8 \ \mathrm {m / s^{2} }\)，水の密度は\(\rho =1000 \ \mathrm {kg / m^{3}}\)とする。

(a)　ペルトン水車の流量の値\(\mathrm {[m^{3} / s ]}\)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　3　　(2)　4　　(3)　5　　(4)　6　　(5)　7

(b)　水車出力の値\(\mathrm {[kW ]}\)として，最も近いものを次の(1)～(5)のうちから一つ選べ。
ただし，\(\mathrm {A}\)点から水車までの水路損失は無視できるものとし，また水車効率は\(88.5 \ ％\)とする。

　(1)　13000　　(2)　14000　　(3)　15000　　(4)　16000　　(5)　17000

【ワンポイント解説】

水車に出力やベルヌーイの定理等の基本公式を使いこなす能力が求められる問題です。本問ではベルヌーイの定理が与えられていますが，重要公式なので確実に記憶しておくようにしましょう。

1.断面積\( \ A \ \mathrm {[m^{2}]} \ \)と流速\( \ v \ \mathrm {[m / s ]} \ \)と流量\( \ Q \ \mathrm {[m^{3} / s ]} \ \)の関係
断面積\( \ A \ \mathrm {[m^{2}]} \ \)の配管内を流速\( \ v \ \mathrm {[m / s ]} \ \)で水が流れている時，配管内を流れる水の流量\( \ Q \ \mathrm {[m^{3} / s ]} \ \)は，
\[
\begin{eqnarray}
Q&=&Av \\[ 5pt ] \end{eqnarray}
\] となります。

2.ベルヌーイの定理
位置水頭が\( \ h \ \)，圧力水頭が\( \ \displaystyle \frac {p}{\rho g} \ \)，速度水頭が\( \ \displaystyle \frac {v^{2}}{2g} \ \)で表されるとき，これらの総和はエネルギー保存則によりどの場所でも等しくなります。
\[
\begin{eqnarray}
h+\frac {p}{\rho g}+\frac {v^{2}}{2g}&=&一定 \\[ 5pt ] \end{eqnarray}
\]

3.水車の出力
有効落差が\( \ H \ \mathrm {[m]} \ \)，流量が\( \ Q \ \mathrm {[m^{3} / s ]} \ \)，水車の効率が\( \ \eta \ \)であるとき，水車の出力\( \ P \ \mathrm {[kW]} \ \)は，
\[
\begin{eqnarray}
P&=&9.8QH\eta \\[ 5pt ] \end{eqnarray}
\] となります。

【関連する「電気の神髄」記事】

　　水力発電の計算における基本式

【解答】

(a)解答：(4)
鉄管断面の半径\(r\)は，
\[
\begin{eqnarray}
r&=&\frac {1.2}{2} \\[ 5pt ] &=&0.6 \ \mathrm {[m ]} \\[ 5pt ] \end{eqnarray}
\] であるから，鉄管の断面積\(A\)は，
\[
\begin{eqnarray}
A&=&\pi r^{2} \\[ 5pt ] &=&\pi \times 0.6^{2} \\[ 5pt ] &≒&1.1310 \ \mathrm {[m^{2} ]} \\[ 5pt ] \end{eqnarray}
\] となるので，ワンポイント解説「1.断面積\(A\)と流速\(v\)と流量\(Q\)の関係」より，ペルトン水車の流量\(Q\)は，
\[
\begin{eqnarray}
Q&=&Av \\[ 5pt ] &=&1.1310 \times 5.3 \\[ 5pt ] &=&5.9943　→　6 \ \mathrm {[m^{3} / s ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(4)
ワンポイント解説「2.ベルヌーイの定理」により，\(\mathrm {A}\)点における有効落差\(H\)は，
\[
\begin{eqnarray}
H&=&h+\frac {p}{\rho g}+\frac {v^{2}}{2g} \\[ 5pt ] &=&0+\frac {3000\times 10^{3}}{1000\times 9.8}+\frac {5.3^{2}}{2\times 9.8} \\[ 5pt ] &≒&307.55 \ \mathrm {[m]} \\[ 5pt ] \end{eqnarray}
\] となるので，ワンポイント解説「3.水車の出力」より，水車の出力\(P \ \mathrm {[kW]}\)は，
\[
\begin{eqnarray}
P&=&9.8QH\eta \\[ 5pt ] &=&9.8\times 5.9943\times 307.55 \times 0.885 \\[ 5pt ] &≒&15989　→　16000 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。