《電力》〈配電〉[H28:問13]単相2線式の電圧降下に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

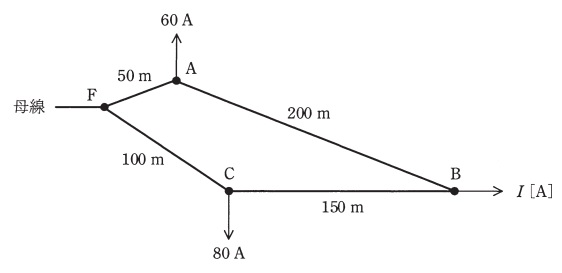
図のような単相\( \ 2 \ \)線式線路がある。母線\( \ \mathrm {F} \ \)点の線間電圧が\( \ \mathrm {107 \ V} \ \)のとき，\( \ \mathrm {B} \ \)点の線間電圧が\( \ \mathrm {96 \ V} \ \)になった。\( \ \mathrm {B} \ \)点の負荷電流\( \ I \ \mathrm { [ A ] } \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。
ただし，使用する電線は全て同じものを用い，電線\( \ 1 \ \)条当たりの抵抗は，\( \ \mathrm {1 \ km} \ \)当たり\( \ \mathrm {0.6 \ \Omega } \ \)とし，抵抗以外は無視できるものとする。また，全ての負荷の力率は\( \ \mathrm {100 \ ％} \ \)とする。

　(1)　\( \ 29.3 \ \)　　(2)　\( \ 54.3 \ \)　　(3)　\( \ 84.7 \ \)　　(4)　\( \ 102.7 \ \)　　(5)　\( \ 121.3 \ \)

【ワンポイント解説】

問9と類題になりますが，三相3線式と単相2線式では電圧降下の式が変わります。それ以外は，一般的な回路計算と変わらず解くことができます。

1.単相2線式配電線路の電圧降下
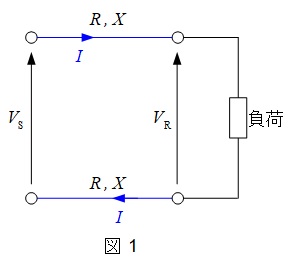
単相2線式の回路の電圧降下は，図1のように負荷との往復分があるので，
\[
\begin{eqnarray}
\varepsilon &=&2I ( R\cos \theta +X \sin \theta ) \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(1)
各送電線路の抵抗は，
\[
\begin{eqnarray}
\mathrm {F-A }：0.6\times \frac {50}{1000} &=&0.03 \ \mathrm {[ \Omega ]} \\[ 5pt ] \mathrm {A-B }：0.6\times \frac {200}{1000} &=&0.12 \ \mathrm {[ \Omega ]} \\[ 5pt ] \mathrm {F-C }：0.6\times \frac {100}{1000} &=&0.06 \ \mathrm {[ \Omega ]} \\[ 5pt ] \mathrm {C-B }：0.6\times \frac {150}{1000} &=&0.09 \ \mathrm {[ \Omega ]} \\[ 5pt ] \end{eqnarray}
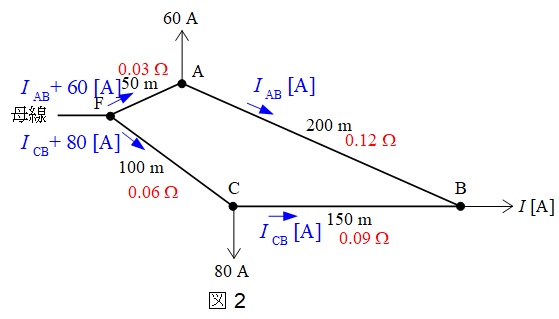
\] となるので，\( \ \mathrm {A-B } \ \)間の電流を\( \ I_{\mathrm {AB}} \ \)，\( \ \mathrm {C-B } \ \)間の電流を\( \ I_{\mathrm {CB}} \ \)とすると，各部の電流値は図2の通りとなる。また，\( \ \mathrm {F} \ \)点から\( \ \mathrm {B} \ \)点の電圧降下は，
\[
\begin{eqnarray}
107-96 &=&11 \ \mathrm {[ V ]} \\[ 5pt ] \end{eqnarray}
\] となる。本問において，力率が\( \ \mathrm {100 \ ％} \ \)であるので，ワンポイント解説「1.単相\( \ 2 \ \)線式配電線路の電圧降下」の式で\( \ \cos \theta =1 \ \)，\( \ \sin \theta =0 \ \)となる。よって，\( \ \mathrm {F→A→B} \ \)と，\( \ \mathrm {F→C→B} \ \)の電圧降下の方程式から，

①\( \ \mathrm {F→A→B} \ \)
\[
\begin{eqnarray}
&11& &=& 2\times \left( I_{\mathrm {AB}}+60 \right) \times 0.03 + 2\times I_{\mathrm {AB}} \times 0.12 \\[ 5pt ] 0.3 &I_{\mathrm {AB}}& &=&11-3.6 \\[ 5pt ] &I_{\mathrm {AB}}& &≒&24.67 \ \mathrm {[ A ]} \\[ 5pt ] \end{eqnarray}
\]

②\( \ \mathrm {F→C→B} \ \)
\[
\begin{eqnarray}
&11& &=& 2\times \left( I_{CB}+80 \right) \times 0.06 + 2\times I_{\mathrm {CB}} \times 0.09 \\[ 5pt ] 0.3 &I_{\mathrm {CB}}& &=&11-9.6 \\[ 5pt ] &I_{\mathrm {CB}}& &≒&4.67 \ \mathrm {[ A ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。したがって，\( \ \mathrm {B} \ \)点の電流\( \ I \ \)は，
\[
\begin{eqnarray}
I &=& I_{\mathrm {AB}} + I_{\mathrm {CB}} \\[ 5pt ] &=&24.67 +4.67 \\[ 5pt ] &≒&29.3 \ \mathrm {[ A ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。