Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
一次側定格電圧と二次側定格電圧がそれぞれ等しい変圧器\( \ \mathrm{A} \ \)と変圧器\( \ \mathrm{B} \ \)がある。変圧器\( \ \mathrm{A} \ \)は,定格容量\( \ S_{\mathrm{A}} =5 \ 000 \ \mathrm{kV\cdot A } \ \),パーセントインピーダンス\( \ %Z_{\mathrm{A}} =9.0 \ % \ \) (自己容量ベース),変圧器\( \ \mathrm{B} \ \)は,定格容量\( \ S_{\mathrm{B}}=1 \ 500 \ \mathrm{kV\cdot A } \ \),パーセントインピーダンス\( \ %Z_{\mathrm{B}} =7.5 \ % \ \) (自己容量ベース)である。この変圧器\( \ 2 \ \)台を並行運転し,\( \ 6 \ 000 \ \mathrm{kV\cdot A } \ \)の負荷に供給する場合,過負荷となる変圧器とその変圧器の過負荷運転状態\( \ \mathrm{ [ % ] } \ \)(当該変圧器が負担する負荷の大きさをその定格容量に対する百分率で表した値)の組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{array}{ccc}
& 過負荷となる変圧器 & 過負荷運転状態 \ \mathrm {[%]} \\
\hline
(1) & 変圧器 \ \mathrm {A} & 101.5 \\
\hline
(2) & 変圧器 \ \mathrm {B} & 105.9 \\
\hline
(3) & 変圧器 \ \mathrm {A} & 118.2 \\
\hline
(4) & 変圧器 \ \mathrm {B} & 137.5 \\
\hline
(5) & 変圧器 \ \mathrm {A} & 173.5 \\
\hline
\end{array}
\]
【ワンポイント解説】
パーセントインピーダンスの問題は慣れるまでは分かりにくいですが,慣れてしまえば他の回路計算とそれほど変わらず解けるようになります。二種以上を目指す場合には故障計算で必要となりますので,容量基準を揃えた場合のパーセントインピーダンスの計算はマスターしておいて下さい。
1.オーム法からパーセントインピーダンス法への変換
基準容量を\( \ P_{\mathrm {n}} \ \mathrm {[V\cdot A]} \ \),基準電圧を\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \),基準電流を\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)とすると,\( \ Z \ \mathrm {[\Omega ]} \ \)の百分率インピーダンス(パーセントインピーダンス)\( \ %Z \ \mathrm {[%]} \ \)は,
\[
\begin{eqnarray}
%Z&=&\frac {ZI_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}\times 100 (定義) \\[ 5pt ]
&=&\frac {\sqrt {3}ZI_{\mathrm {n}}}{V_{\mathrm {n}}}\times 100 \\[ 5pt ]
&=&\frac {\sqrt {3}ZV_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}}\times 100 \\[ 5pt ]
&=&\frac {P_{\mathrm {n}}Z}{V_{\mathrm {n}}^{2}}\times 100 (∵P_{\mathrm {n}}=\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} ) \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.百分率インピーダンスの容量換算
「1.オーム法からパーセントインピーダンス法への変換」の通り,百分率インピーダンスは基準容量に比例します。したがって,基準容量\( \ P_{\mathrm {A}} \ \mathrm {[V\cdot A]} \ \)の時\( \ %Z_{\mathrm {A}} \ \mathrm {[%]} \ \)のインピーダンスを\( \ P_{\mathrm {B}} \ \mathrm {[V\cdot A]} \ \)へ換算した百分率インピーダンス\( \ %Z_{\mathrm {B}} \ \mathrm {[%]} \ \)は,
\[
\begin{eqnarray}
%Z_{\mathrm {B}}&=&\frac {P_{\mathrm {B}}}{P_{\mathrm {A}}}%Z_{\mathrm {A}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.変圧器の負荷分担
並行運転の条件を満たす同じ基準容量の元での百分率インピーダンス\( \ %Z_{\mathrm {A}} \ \mathrm {[%]} \ \)の変圧器\( \ \mathrm {A} \ \)と百分率インピーダンス\( \ %Z_{\mathrm {B}} \ \mathrm {[%]} \ \)の変圧器\( \ \mathrm {B} \ \)があり,負荷\( \ P \ \mathrm {[W]} \ \)を接続するとき,それぞれの負荷分担\( \ P_{\mathrm {A}} \ \mathrm {[W]} \ \)及び\( \ P_{\mathrm {B}} \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {A}}&=&\frac {%Z_{\mathrm {B}}}{%Z_{\mathrm {A}}+%Z_{\mathrm {B}}}P \\[ 5pt ]
P_{\mathrm {B}}&=&\frac {%Z_{\mathrm {A}}}{%Z_{\mathrm {A}}+%Z_{\mathrm {B}}}P \\[ 5pt ]
\end{eqnarray}
\]
と求められます。両変圧器とも一次二次電圧が等しいことから,分流の法則が適用できるという解釈で考えると良いかと思います。
【解答】
解答:(2)
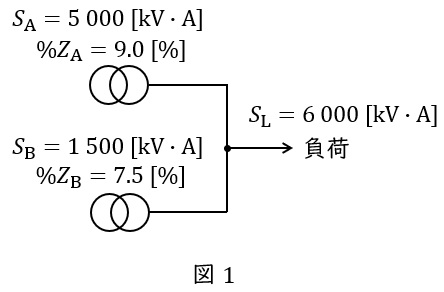
問題文に沿って,変圧器と負荷の関係を図に示すと図1のようになる。
変圧器\( \ \mathrm{B} \ \)の百分率インピーダンス\( \ %Z_{\mathrm{B}}=7.5 \ \mathrm {[%]} \ \)を変圧器\( \ \mathrm{A} \ \)の\( \ S_{\mathrm{A}} =5 \ 000 \ \mathrm {[kV\cdot A]} \ \)換算にしたときの百分率インピーダンス\( \ %Z_{\mathrm {B}}^{\prime } \ \mathrm {[%]} \ \)は,ワンポイント解説「2.百分率インピーダンスの容量換算」の通り,
\[
\begin{eqnarray}
%Z_{\mathrm {B}}^{\prime }&=&\frac {S_{\mathrm{A}}}{S_{\mathrm{B}}}\times %Z_{\mathrm{B}} \\[ 5pt ]
&=&\frac {5 \ 000}{1 \ 500}\times 7.5 \\[ 5pt ]
&=&25 \ \mathrm {[ % ]} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,それぞれの変圧器が負担する容量\( \ P_{\mathrm{A}} \ \mathrm {[kV\cdot A]} \ \)と\( \ P_{\mathrm{B}} \ \mathrm {[kV\cdot A]} \ \)は,ワンポイント解説「3.変圧器の負荷分担」の通り,
\[
\begin{eqnarray}
P_{\mathrm{A}}&=&\frac {%Z_{\mathrm{B}}^{\prime }}{%Z_{\mathrm{A}}+%Z_{\mathrm{B}}^{\prime }}P_{\mathrm{L}} \\[ 5pt ]
&=& \frac {25}{9.0 +25} \times 6 \ 000 \\[ 5pt ]
&≒&4 \ 412 \ \mathrm {[ kV\cdot A ]} \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
P_{\mathrm{B}}&=&\frac {%Z_{\mathrm{A}}}{%Z_{\mathrm{A}}+%Z_{\mathrm{B}}^{\prime }}P_{\mathrm{L}} \\[ 5pt ]
&=&\frac {9.0}{9.0 +25} \times 6 \ 000 \\[ 5pt ]
&≒&1 \ 588 \ \mathrm {[ kV\cdot A ]} \\[ 5pt ]
\end{eqnarray}
\]
となる。従って,過負荷となる変圧器は変圧器\( \ \mathrm{B} \ \)であり,その過負荷運転状態\( \ \mathrm{ [ % ] } \ \) は,
\[
\begin{eqnarray}
\frac {P_{\mathrm{B}}}{S_{\mathrm{B}}}\times 100&=&\frac {1 \ 588}{1 \ 500}\times 100 \\[ 5pt ]
&≒& 105.9 \ \mathrm{ [ % ] } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは