《電力》〈変電〉[H30:問12]変圧器のV結線方式に関する論説問題

【問題】

【難易度】★★★☆☆（普通）

変圧器の\(\mathrm {V}\)結線方式に関する記述として，誤っているものを次の(1)～(5)のうちから一つ選べ。

(1)　単相変圧器2台で三相が得られる。

(2)　同一の変圧器2台を使用して三相平衡負荷に供給している場合，\(\Delta \)結線変圧器と比較して，出力は\(\displaystyle \frac {\sqrt{3}}{2}\)倍となる。

(3)　同一の変圧器2台を使用して三相平衡負荷に供給している場合，変圧器の利用率は\(\displaystyle \frac {\sqrt{3}}{2}\)となる。

(4)　電灯動力共用方式の場合，共用変圧器には電灯と動力の電流が加わって流れるため，一般に動力専用変圧器の容量と比較して共用変圧器の容量の方が大きい。

(5)　単相変圧器を用いた\(\Delta \)結線方式と比較して，変圧器の電柱への設置が簡素化できる。

【ワンポイント解説】

ぱっと見て(2)か(3)のどちらかが間違いであると分かれば，かなり勉強は進んでいると考えて良いと思います。\(\mathrm {V}\)結線のベクトル図は電験二種以上のレベルの内容となりますが，出力比や利用率を検討する際には参考になさって下さい。ただし，丸暗記でも問題ありません。

1.\(\mathrm {V}\)結線の最大出力と最大利用率
①\(\Delta \)結線
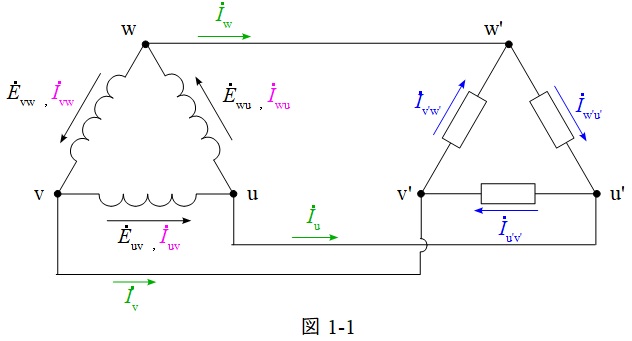
図1-1に示すような\(\Delta \)結線の変圧器が三相平衡負荷（簡単のため抵抗のみとする）で力率\(1\)で運転しているものとすると，\({\dot E}_{\mathrm {uv}}\)と\({\dot I}_{\mathrm {u^{\prime }v^{\prime }}}\)，\({\dot E}_{\mathrm {vw}}\)と\({\dot I}_{\mathrm {v^{\prime }w^{\prime }}}\)，\({\dot E}_{\mathrm {wu}}\)と\({\dot I}_{\mathrm {w^{\prime }u^{\prime }}}\)の位相は等しくなり，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {u}} &=&{\dot I}_{\mathrm {u^{\prime }v^{\prime }}}-{\dot I}_{\mathrm {w^{\prime }u^{\prime }}} &=&{\dot I}_{\mathrm {uv}}-{\dot I}_{\mathrm {wu}} \\[ 5pt ] {\dot I}_{\mathrm {v}} &=&{\dot I}_{\mathrm {v^{\prime }w^{\prime }}}-{\dot I}_{\mathrm {u^{\prime }v^{\prime }}} &=&{\dot I}_{\mathrm {vw}}-{\dot I}_{\mathrm {uv}} \\[ 5pt ] {\dot I}_{\mathrm {w}} &=&{\dot I}_{\mathrm {w^{\prime }u^{\prime }}}-{\dot I}_{\mathrm {v^{\prime }w^{\prime }}} &=&{\dot I}_{\mathrm {wu}}-{\dot I}_{\mathrm {vw}} \\[ 5pt ] \end{eqnarray}
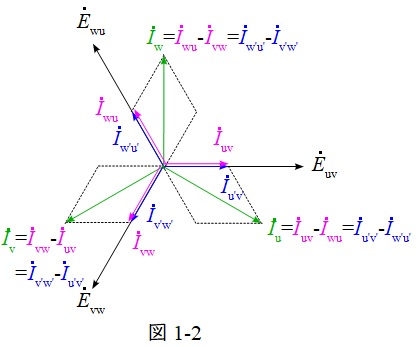
\] の関係より，ベクトル図は図1-2のように描けます。よって，変圧器の定格電圧定格電流での出力\(P_{\Delta }\)は，変圧器１台の出力を\(P\)とすると，
\[
\begin{eqnarray}
P_{\Delta } &=&3\times \left| {\dot E}_{\mathrm {uv}}\right| \left| {\dot I}_{\mathrm {uv}}\right| \\[ 5pt ] &=&3P \\[ 5pt ] \end{eqnarray}
\] となり，設備利用率\(\eta \)は，
\[
\begin{eqnarray}
\eta &=&\frac {P_{\Delta }}{3P}\times 100 \\[ 5pt ] &=&100 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] となります。

②\(\mathrm {V}\)結線
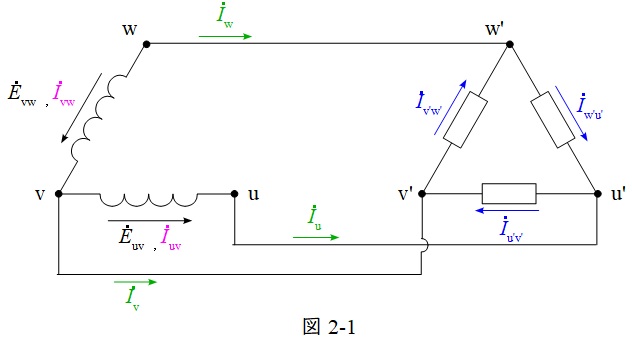
図2-1に示すような\(\mathrm {V}\)結線の変圧器が三相平衡負荷（簡単のため抵抗のみとする）で力率\(1\)で運転しているものとすると，\({\dot E}_{\mathrm {uv}}\)と\({\dot I}_{\mathrm {u^{\prime }v^{\prime }}}\)，\({\dot E}_{\mathrm {vw}}\)と\({\dot I}_{\mathrm {v^{\prime }w^{\prime }}}\)，\({\dot E}_{\mathrm {wu}}\)と\({\dot I}_{\mathrm {w^{\prime }u^{\prime }}}\)の位相は等しくなり，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {u}} &=&{\dot I}_{\mathrm {u^{\prime }v^{\prime }}}-{\dot I}_{\mathrm {w^{\prime }u^{\prime }}} \\[ 5pt ] {\dot I}_{\mathrm {v}} &=&{\dot I}_{\mathrm {v^{\prime }w^{\prime }}}-{\dot I}_{\mathrm {u^{\prime }v^{\prime }}} \\[ 5pt ] {\dot I}_{\mathrm {w}} &=&{\dot I}_{\mathrm {w^{\prime }u^{\prime }}}-{\dot I}_{\mathrm {v^{\prime }w^{\prime }}} \\[ 5pt ] \end{eqnarray}
\] \[
\begin{eqnarray}
{\dot I}_{\mathrm {u}} &=&{\dot I}_{\mathrm {u^{\prime }v^{\prime }}} \\[ 5pt ] {\dot I}_{\mathrm {w}} &=&-{\dot I}_{\mathrm {v^{\prime }w^{\prime }}} \\[ 5pt ] \end{eqnarray}
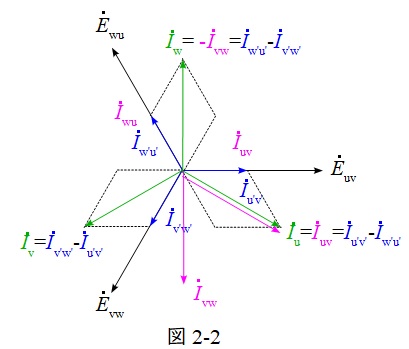
\] の関係より，ベクトル図は図2-2のように描けます。よって，変圧器の定格電圧定格電流での出力\(P_{\mathrm {V}}\)は，変圧器１台の出力を\(P\)とすると，
\[
\begin{eqnarray}
P_{\mathrm {V}} &=&2\times \left| {\dot E}_{\mathrm {uv}}\right| \left| {\dot I}_{\mathrm {uv}}\right| \cos \frac {\pi }{6}\\[ 5pt ] &=&\sqrt {3} P \\[ 5pt ] \end{eqnarray}
\] となり，設備利用率\(\eta \)は，
\[
\begin{eqnarray}
\eta &=&\frac {P_{\mathrm {V}}}{2P}\times 100 \\[ 5pt ] &=&\frac {\sqrt {3} P}{2P}\times 100 \\[ 5pt ] &=&86.6 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(2)
(1)：正しい
問題文の通り，\(\mathrm {V}\)結線は単相変圧器2台で三相が得られます。

(2)：誤り
ワンポイント解説「1.\(\mathrm {V}\)結線の最大出力と最大利用率」の通り，\(\mathrm {V}\)結線の最大出力は\(\sqrt {3}P\)，\(\Delta \)結線の最大出力は\(3P\)なので，出力比は，
\[
\begin{eqnarray}
\frac {P_{\mathrm {V}}}{P_{\Delta }} &=&\frac {\sqrt {3}}{3} \\[ 5pt ] \end{eqnarray}
\] となります。

(3)：正しい
ワンポイント解説「1.\(\mathrm {V}\)結線の最大出力と最大利用率」の通り，\(\mathrm {V}\)結線の利用率は\(\displaystyle \frac {\sqrt{3}}{2}\)となります

(4)：正しい
問題文の通りです。電灯動力共用方式の場合，共用変圧器には電灯と動力の電流が加わって流れるため，一般に動力専用変圧器の容量と比較して共用変圧器の容量の方が大きくなります。

(5)：正しい
問題文の通り，単相変圧器を用いた\(\Delta \)結線方式と比較すると変圧器の台数も少ないので，変圧器の電柱への設置が簡素化できます。