《電力》〈配電〉[H30:問8]平衡三相負荷への供給電力に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

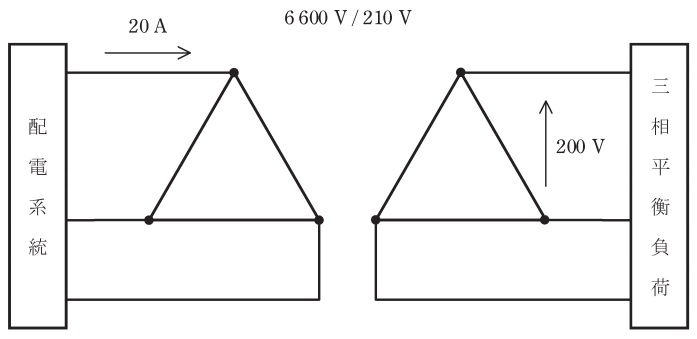
図のように，単相の変圧器\(3\)台を一次側，二次側ともに\(\Delta \)結線し，三相対称電源とみなせる配電系統に接続した。変圧器の一次側の定格電圧は\( \ 6600 \ \mathrm {V} \ \)，二次側の定格電圧は\( \ 210 \ \mathrm {V} \ \)である。二次側に三相平衡負荷を接続したときに，一次側の線電流\( \ 20 \ \mathrm {A} \ \)，二次側の線間電圧\( \ 200 \ \mathrm {V} \ \)であった。負荷に供給されている電力\( \ \mathrm {[kW]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。ただし，負荷の力率は\(0.8\)とする。なお，変圧器は理想変圧器とみなすことができ，線路のインピーダンスは無視することができる。

　(1)　\(58\)　　(2)　\(101\)　　(3)　\(174\)　　(4)　\(218\)　　(5)　\(302\)

【ワンポイント解説】

内容としては三相交流の電力を求める公式を知っていれば解ける問題です。\(\sqrt {3}\)や力率\(\cos \theta \)を掛け忘れないかが重要となりそうです。

1.三相交流回路の電力\(P\)
平衡三相回路の負荷の消費電力\(P\)は，二次側の線間電圧\(V\)，二次側の線電流\(I\)，負荷の力率\(\cos \theta \)とすると，
\[
\begin{eqnarray}
P &=&\sqrt {3}VI\cos \theta \\[ 5pt ] \end{eqnarray}
\] で求められます。

【解答】

解答：(3)
一次側の線電流\( \ I_{1}= 20 \ \mathrm {A} \ \)であるから，二次側の線電流\(I_{2}\)は，
\[
\begin{eqnarray}
I_{2} &=&\frac {6600}{210}\times I_{1} \\[ 5pt ] &=&\frac {6600}{210}\times 20 \\[ 5pt ] &≒&628.57 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。二次側の線間電圧\( \ V_{2}= 200 \ \mathrm {V} \ \)，力率\( \cos \theta =0.8 \ \)であるから，ワンポイント解説「1.三相交流回路の電力\(P\)」より，負荷に供給されている電力\(P\)は，
\[
\begin{eqnarray}
P &=&\sqrt {3}V_{2}I_{2}\cos \theta \\[ 5pt ] &=&\sqrt {3}\times 200 \times 628.57 \times 0.8 \\[ 5pt ] &≒&174194 \ \mathrm {[W]}　→　174 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。