Contents
【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,配電線路に用いられる柱上変圧器に関する記述である。
柱上に設置される変圧器としては,容量\( \ \fbox { (ア) } \ \)のものが多く使用されている。
鉄心には,けい素鋼板が多く使用されているが,\( \ \fbox { (イ) } \ \)のために鉄心にアモルファス金属材料を用いた変圧器も使用されている。
また,変圧器保護のために,\( \ \fbox { (ウ) } \ \)を柱上変圧器に内蔵したものも使用されている。
三相\( \ 3 \ \)線式\( \ 200 \ \mathrm {V} \ \)に供給するときの結線には,\( \ \Delta \ \)結線と\( \ \mathrm {V} \ \)結線がある。\( \ \mathrm {V} \ \)結線は単相変圧器\( \ 2 \ \)台によって構成できるため,\( \ \Delta \ \)結線よりも変圧器の電柱への設置が簡素化できるが,同一容量の単相変圧器\( \ 2 \ \)台を使用して三相平衡負荷に供給している場合,同一容量の単相変圧器\( \ 3 \ \)台を使用した\( \ \Delta \ \)結線と比較して,出力は\( \ \fbox { (エ) } \ \)倍となる。
上記の記述中の空白箇所(ア)~(エ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{array}{ccccc}
& (ア) & (イ) & (ウ) & (エ) \\
\hline
(1) & 10~100 \ \mathrm {kV\cdot A} & 小型化 & 漏電遮断器 & \displaystyle \frac {1}{\sqrt {3}} \\
\hline
(2) & 10~30 \ \mathrm {MV\cdot A} & 低損失化 & 漏電遮断器 & \displaystyle \frac {\sqrt {3}}{2} \\
\hline
(3) & 10~30 \ \mathrm {MV\cdot A} & 低損失化 & 避雷器 & \displaystyle \frac {\sqrt {3}}{2} \\
\hline
(4) & 10~100 \ \mathrm {kV\cdot A} & 低損失化 & 避雷器 & \displaystyle \frac {1}{\sqrt {3}} \\
\hline
(5) & 10~100 \ \mathrm {kV\cdot A} & 小型化 & 避雷器 & \displaystyle \frac {\sqrt {3}}{2} \\
\hline
\end{array}
\]
【ワンポイント解説】
配電線路で使用される柱上変圧器に関する問題です。
街中の電柱にも設置されている変圧器なので,イメージもしやすいかと思います。
下記の\( \ \mathrm {V-V} \ \)結線の設備利用率と容量は\( \ 3 \ \)種の場合は覚えておくだけでも良いかもしれませんが,\( \ 2 \ \)種以上を目指す場合にはその中身も理解しておくと良いと思います。
1.\( \ \mathrm {\Delta -\Delta } \ \)結線と\( \ \mathrm {V-V} \ \)結線の比較
①\( \ \mathrm {\Delta -\Delta } \ \)結線
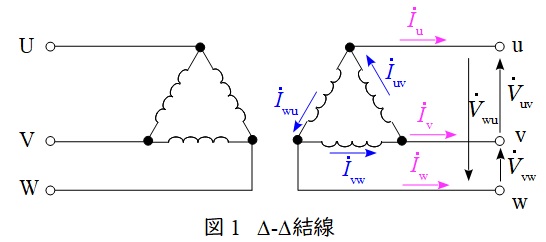
\( \ \mathrm {\Delta -\Delta } \ \)結線の変圧器の回路図とベクトル図を図1及び図2に示します。
図1において,負荷電流\( \ {\dot I}_{\mathrm {u}} \ \mathrm {[A]} \ \)は,変圧器を流れる電流\( \ {\dot I}_{\mathrm {uv}} \ \mathrm {[A]} \ \)及び\( \ {\dot I}_{\mathrm {wu}} \ \mathrm {[A]} \ \)を用いて,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {u}}&=& {\dot I}_{\mathrm {uv}}-{\dot I}_{\mathrm {wu}} \\[ 5pt ]
\end{eqnarray}
\]
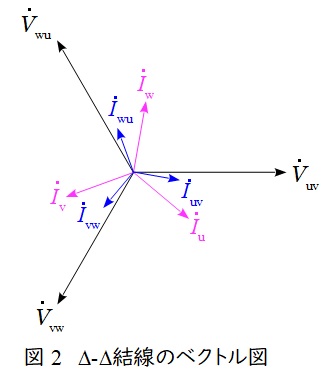
で求められ,ベクトル図上では図2のような関係となり,三相平衡である場合にはそれぞれの大きさの比は,
\[
\begin{eqnarray}
I_{\mathrm {u}}&=& \sqrt {3}I_{\mathrm {uv}} \\[ 5pt ]
\end{eqnarray}
\]
であることが分かります。したがって,各変圧器が分担する容量\( \ S \ \mathrm {[V\cdot A]} \ \)は,負荷の線間電圧を\( \ V_{\mathrm {uv}}=V_{\mathrm {vw}}=V_{\mathrm {wu}}=V \ \),負荷電流を\( \ I_{\mathrm {u}}=I_{\mathrm {v}}=I_{\mathrm {w}}=I \ \)とすると,
\[
\begin{eqnarray}
S&=& \frac {VI}{\sqrt {3}} \\[ 5pt ]
\end{eqnarray}
\]
となります。したがって,変圧器全体の送電電力\( \ P \ \mathrm {[W]} \ \)は力率を\( \ \cos \theta \ \)とすると,
\[
\begin{eqnarray}
P&=& 3S\cos \theta \\[ 5pt ]
&=& 3\cdot \frac {VI}{\sqrt {3}}\cdot \cos \theta \\[ 5pt ]
&=&\sqrt {3}VI \cos \theta \\[ 5pt ]
\end{eqnarray}
\]
となります。
②\( \ \mathrm {V -V } \ \)結線
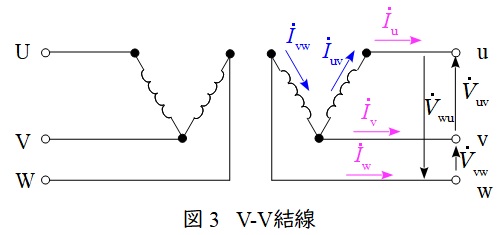
\( \ \mathrm {V -V } \ \)結線の変圧器の回路図とベクトル図を図3及び図4に示します。
図3において,負荷電流\( \ {\dot I}_{\mathrm {u}} \ \mathrm {[A]} \ \),\( \ {\dot I}_{\mathrm {v}} \ \mathrm {[A]} \ \),\( \ {\dot I}_{\mathrm {w}} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {u}}&=& {\dot I}_{\mathrm {uv}} \\[ 5pt ]
{\dot I}_{\mathrm {v}}&=& {\dot I}_{\mathrm {vw}}-{\dot I}_{\mathrm {uv}} \\[ 5pt ]
{\dot I}_{\mathrm {w}}&=& -{\dot I}_{\mathrm {vw}} \\[ 5pt ]
\end{eqnarray}
\]
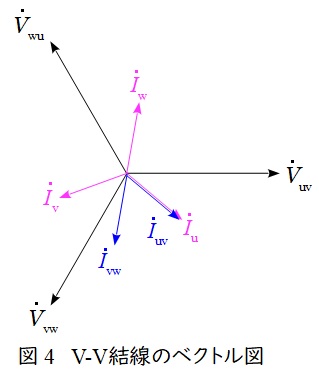
で求められ,ベクトル図上では図4のような関係となり,三相平衡である場合にはそれぞれの大きさの比は,
\[
\begin{eqnarray}
I_{\mathrm {u}}&=&I_{\mathrm {v}}&=&I_{\mathrm {w}}&=&I_{\mathrm {uv}}&=&I_{\mathrm {vw}} \\[ 5pt ]
\end{eqnarray}
\]
であることが分かります。したがって,各変圧器が分担する容量\( \ S \ \mathrm {[V\cdot A]} \ \)は,負荷の線間電圧を\( \ V_{\mathrm {uv}}=V_{\mathrm {vw}}=V_{\mathrm {wu}}=V \ \),負荷電流を\( \ I_{\mathrm {u}}=I_{\mathrm {v}}=I_{\mathrm {w}}=I \ \)とすると,
\[
\begin{eqnarray}
S&=& VI \\[ 5pt ]
\end{eqnarray}
\]
となります。変圧器全体の送電電力\( \ P_{\mathrm {V}} \ \mathrm {[W]} \ \)は力率を\( \ \cos \theta \ \)とすると,
\[
\begin{eqnarray}
P_{\mathrm {V}}&=& \sqrt {3}VI \cos \theta \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ \mathrm {V -V } \ \)結線で得られる出力\( \ \mathrm {[V\cdot A]} \ \)は各変圧器の出力の\( \ \sqrt {3} \ \)倍となるため,利用率は,
\[
\begin{eqnarray}
利用率&=& \frac {\sqrt {3}VI}{2VI} \\[ 5pt ]
&=& \frac {\sqrt {3}}{2} → 86.6 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
となります。また,\( \ \mathrm {V -V } \ \)結線と\( \ \mathrm {\Delta -\Delta } \ \)結線で同じ電力を出力する場合に必要となる変圧器の容量比は,
\[
\begin{eqnarray}
容量比&=& \frac {\displaystyle \frac {VI}{\sqrt {3}}}{VI} \\[ 5pt ]
&=& \frac {1}{\sqrt {3}} → 57.7 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
となるため,\( \ \mathrm {V -V } \ \)結線の出力は\( \ \mathrm {\Delta -\Delta } \ \)結線の\( \ 57.7 \ \mathrm {[%]} \ \)程度であることがわかります。
【解答】
解答:(4)
(ア)
結論からいうと\( \ 10~100 \ \mathrm {kV\cdot A} \ \)ですが,仮に\( \ 30 \ \mathrm {MV\cdot A} \ \)で\( \ 6.6 \ \mathrm {kV} \ \)であった場合,電流は数千アンペアも流れることになるため現実的ではありません。なので,丸暗記だけでなく予想も立てられると良いと思います。
(イ)
アモルファス変圧器を採用することで,低損失化を図ることができます。小型化は容量が小さい場合に\( \ \mathrm {V -V } \ \)結線としたときの\( \ \mathrm {\Delta -\Delta } \ \)結線に対するメリットの一つです。
(ウ)
柱上変圧器の最大のリスク要因となるのは雷による過電圧なので,変圧器保護のために設置されるものは避雷器となります。漏電遮断器は,漏電による感電事故や火災を防止するための機器で,変圧器よりも機械設備に設けられることが多い機器となります。
(エ)
ワンポイント解説「1.\( \ \mathrm {\Delta -\Delta } \ \)結線と\( \ \mathrm {V-V} \ \)結線の比較」の通り,\( \ \mathrm {V} \ \)結線の出力は\( \ \Delta \ \)結線の\( \ \displaystyle \frac {1}{\sqrt {3}} \ \)倍となります。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは