《電力》〈配電〉[R4下:問17]不平衡負荷を接続した単相３線式配電線路に関する計算問題

【問題】

【難易度】★★★★★（難しい）

図のように配電用変圧器二次側の単相\( \ 3 \ \)線式低圧配電線路に負荷\( \ \mathrm {A} \ \)及び負荷\( \ \mathrm {B} \ \)が接続されている場合について，次の(a)及び(b)の問に答えよ。ただし，変圧器は，励磁電流，内部電圧降下及び内部損失などを無視できる理想変圧器で，一次電圧は\( \ 6 \ 600 \ \mathrm {V} \ \)，二次電圧は\( \ 110 / 220 \ \mathrm {V} \ \)で一定であるものとする。また，低圧配電線路及び中性線の電線\( \ 1 \ \)線当たりの抵抗は\( \ 0.06 \ \mathrm {\Omega } \ \)，負荷\( \ \mathrm {A} \ \)及び負荷\( \ \mathrm {B} \ \)は純抵抗負荷とし，これら以外のインピーダンスは考慮しないものとする。

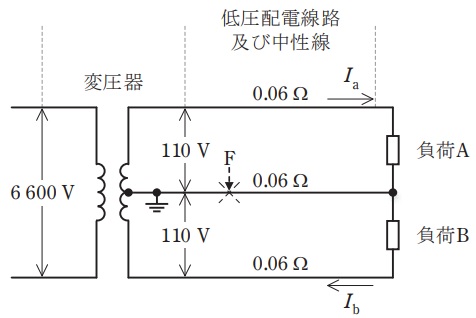
(a)　変圧器の電流を測定したところ，一次電流が\( \ 5 \ \mathrm {A} \ \)，二次電流\( \ I_{\mathrm {a}} \ \)と\( \ I_{\mathrm {b}} \ \)の比が\( \ 2 : 3 \ \)あった。二次側低圧配電線路及び中性線における損失の合計値\( \ \mathrm {[kW]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 2.59 \ \)　　(2)　\( \ 2.81 \ \)　　(3)　\( \ 3.02 \ \)　　(4)　\( \ 5.83 \ \)　　(5)　\( \ 8.21 \ \)

(b) 低圧配電線路の中性線が点\( \ \mathrm {F} \ \)で断線した場合に負荷\( \ \mathrm {A} \ \)にかかる電圧の値\( \ \mathrm {[V]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 88 \ \)　　(2)　\( \ 106 \ \)　　(3)　\( \ 123 \ \)　　(4)　\( \ 127 \ \)　　(5)　\( \ 138 \ \)

【ワンポイント解説】

単相\( \ 3 \ \)線式配電線路の線路計算に関する問題です。
単相\( \ 3 \ \)線式線路の特徴を理解する上ではとても良い問題と思いますが，問16と共に難易度が高く受験生を悩ませる問題であったかなと思います。

1.変圧器の巻数比と変圧比，変流比の関係
変圧器の一次側の巻数\( \ N_{1} \ \)，電圧\( \ V_{1} \ \mathrm {[V]} \ \)，電流\( \ I_{1} \ \mathrm {[A]} \ \)，二次側の巻数\( \ N_{2} \ \)，電圧\( \ V_{2} \ \mathrm {[V]} \ \)，電流\( \ I_{2} \ \mathrm {[A]} \ \)とすると，巻数比\( \ \displaystyle a=\frac {N_{1}}{N_{2}} \ \)は，
\[
\begin{eqnarray}
a&=&\frac {N_{1}}{N_{2}} =\frac {V_{1}}{V_{2}}=\frac {I_{2}}{I_{1}} \\[ 5pt ] \end{eqnarray}
\] となります。不平衡の単相\( \ 3 \ \)線式線路においては，二次電流\( \ I_{\mathrm {2a}} \ \mathrm {[A]} \ \)，\( \ I_{\mathrm {2b}} \ \mathrm {[A]} \ \)であるとすると，
\[
\begin{eqnarray}
V_{1}I_{1}&=&\frac {V_{2}}{2}I_{\mathrm {2a}}+ \frac {V_{2}}{2}I_{\mathrm {2b}} \\[ 5pt ] \end{eqnarray}
\] の関係があります。

【解答】

(a)解答：(3)
一次電圧\( \ V_{1}= 6 \ 600 \ \mathrm {[V]} \ \)，一次電流\( \ I_{1}=5 \ \mathrm {[A]} \ \)，二次電圧\( \ V_{2}= 220 \ \mathrm {[V]} \ \)とおく。変圧器の一次二次皮相電力が等しいことから，ワンポイント解説「1.変圧器の巻数比と変圧比，変流比の関係」の通り，
\[
\begin{eqnarray}
V_{1}I_{1} &=&\frac {V_{2}}{2}I_{\mathrm {a}}+\frac {V_{2}}{2}I_{\mathrm {b}} \\[ 5pt ] \end{eqnarray}
\] であり，題意より\( \ \displaystyle I_{\mathrm {b}}=\frac {3}{2}I_{\mathrm {a}} \ \)であるから，
\[
\begin{eqnarray}
V_{1}I_{1} &=&\frac {V_{2}}{2}I_{\mathrm {a}}+\frac {V_{2}}{2}\cdot \frac {3}{2}I_{\mathrm {a}} \\[ 5pt ] &=&\frac {5}{2}\cdot \frac {V_{2}}{2}I_{\mathrm {a}} \\[ 5pt ] I_{\mathrm {a}}&=&\frac {4V_{1}I_{1}}{5V_{2}} \\[ 5pt ] &=&\frac {4\times 6 \ 600\times 5}{5\times 220} \\[ 5pt ] &=&120 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，\( \ I_{\mathrm {b}} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {b}} &=&\frac {3}{2}I_{\mathrm {a}} \\[ 5pt ] &=&\frac {3}{2}\times 120 \\[ 5pt ] &=&180 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となり，中性線電流\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {n}} &=&I_{\mathrm {b}}-I_{\mathrm {a}} \\[ 5pt ] &=&180-120 \\[ 5pt ] &=&60 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，二次側低圧配電線路及び中性線における損失の合計値\( \ P_{\mathrm {l}} \ \mathrm {[kW]} \ \)は，電線\( \ 1 \ \)線当たりの抵抗が\( \ R=0.06 \ \mathrm {[\Omega ]} \ \)であるから，
\[
\begin{eqnarray}
P_{\mathrm {l}} &=&RI_{\mathrm {a}}^{2}+RI_{\mathrm {b}}^{2}+RI_{\mathrm {n}}^{2} \\[ 5pt ] &=&R\left( I_{\mathrm {a}}^{2}+I_{\mathrm {b}}^{2}+I_{\mathrm {n}}^{2}\right) \\[ 5pt ] &=&0.06\times \left( 120^{2}+180^{2}+60^{2}\right) \\[ 5pt ] &=&3 \ 024 \ \mathrm {[W]}　→　3.02 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(4)
負荷\( \ \mathrm {A} \ \)の抵抗値を\( \ R_{\mathrm {a}} \ \mathrm {[\Omega ]} \ \)，負荷\( \ \mathrm {B} \ \)の抵抗値を\( \ R_{\mathrm {b}} \ \mathrm {[\Omega ]} \ \)とする。
点\( \ \mathrm {F} \ \)で断線する前の条件において，負荷\( \ \mathrm {A} \ \)に加わる電圧\( \ V_{\mathrm {a}} \ \mathrm {[V]} \ \)及び負荷\( \ \mathrm {B} \ \)に加わる電圧\( \ V_{\mathrm {b}} \ \mathrm {[V]} \ \)は，中性線電流\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)が右向きであることに注意すると，
\[
\begin{eqnarray}
V_{\mathrm {a}} &=&110-RI_{\mathrm {a}}+RI_{\mathrm {n}} \\[ 5pt ] &=&110-0.06\times 120+0.06\times 60 \\[ 5pt ] &=&106.4 \ \mathrm {[V]} \\[ 5pt ] V_{\mathrm {b}} &=&110-RI_{\mathrm {b}}-RI_{\mathrm {n}} \\[ 5pt ] &=&110-0.06\times 180-0.06\times 60 \\[ 5pt ] &=&95.6 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] であるため，それぞれの抵抗値\( \ R_{\mathrm {a}} \ \mathrm {[\Omega ]} \ \)及び\( \ R_{\mathrm {b}} \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
R_{\mathrm {a}} &=&\frac {V_{\mathrm {a}}}{I_{\mathrm {a}}} \\[ 5pt ] &=&\frac {106.4}{120} \\[ 5pt ] &≒&0.8867 \ \mathrm {[\Omega ]} \\[ 5pt ] R_{\mathrm {b}} &=&\frac {V_{\mathrm {b}}}{I_{\mathrm {b}}} \\[ 5pt ] &=&\frac {95.6}{180} \\[ 5pt ] &≒&0.5311 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，分圧の法則より，点\( \ \mathrm {F} \ \)で断線した場合に負荷\( \ \mathrm {A} \ \)にかかる電圧\( \ V_{\mathrm {a}}^{\prime } \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {a}}^{\prime } &=&\frac {R_{\mathrm {a}}}{R+R_{\mathrm {a}}+R_{\mathrm {b}}+R}V_{2} \\[ 5pt ] &=&\frac {0.8867}{0.06+0.8867+0.5311+0.06}\times 220 \\[ 5pt ] &≒&127 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。